云南省楚雄州2023-2024学年九年级上学期期中考试数学试卷
试卷更新日期：2023-12-16 类型：期中考试
一、选择题（本大题共12个小题，每小题只有一个正确选项，每小题3分，共36分）
-
1. 一元二次方程x2+x＝0的根是（ ）A、x＝0 B、x＝﹣1 C、x＝0或x＝﹣1 D、x＝±12. 一元二次方程x2﹣x﹣1=0的根的情况为（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 二次函数y＝（x﹣1）2的顶点坐标是（ ）A、（0，﹣1） B、（0，1） C、（﹣1，0） D、（1，0）4. 下列标志图中，既是中心对称图形，又是轴对称图形的是（ ）A、
B、
C、
D、
5. 用配方法解一元二次方程x2﹣6x=﹣5的过程中，配方正确的是（ ）A、（x+3）2=1 B、（x﹣3）2=1 C、（x+3）2=4 D、（x﹣3）2=46. 在平面直角坐标系中，已知点P的坐标是（﹣1，﹣2），则点P关于原点对称的点的坐标是（ ）A、（1，2） B、（1，﹣2） C、（﹣1，2） D、（2，1）7. 已知圆锥的底面半径为4cm，母线长为5cm，则这个圆锥的侧面积是（ ）A、20πcm2 B、20cm2 C、40πcm2 D、40cm28. 如图，是的直径，是上一点．若 ， 则（ ）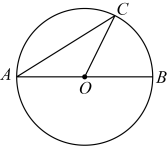
A、 B、 C、 D、9. 已知关于x的方程x2+3x+a=0有一个根为﹣2，则另一个根为（ ）A、5 B、﹣1 C、2 D、﹣510. 二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列说法不正确的是（ ）
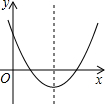A、b2﹣4ac＞0 B、a＞0 C、c＞0 D、11. 在平面直角坐标系中，平行四边形ABCD的对称中心是坐标原点，顶点A、B的坐标分别是（﹣1，1）、（2，1），将平行四边形ABCD沿x轴向左平移3个单位长度，则顶点C的对应点C1的坐标是（ ）A、（﹣2，﹣1） B、（4，﹣1） C、（1，2） D、（2，1）12. 如图，在△OAB中，顶点O（0，0），A（﹣2，3），B（2，3），将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，则第2023次旋转结束时，点D的坐标为（ ）
A、（﹣2，7） B、（7，2） C、（2，﹣7） D、（﹣7，﹣2）二、填空题（本大题共4个小题，每小题2分，共8分）
-
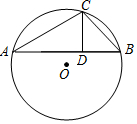
13. 如图，点A ， B ， C在⊙O上，∠ACB＝30°，则∠ABO的度数是 ．
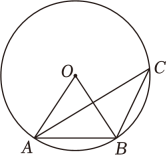14. 已知x1 ， x2是一元二次方程x2﹣2x﹣1=0的两根，则 =15. 若关于x的方程x2﹣2x﹣m＝0有两个实数根，则m的取值范围是 ．16. 已知，⊙O的半径为一元二次方程x2﹣5x﹣6＝0的两根，圆心O到直线l的距离d＝4，则直线l与⊙O的位置关系是 ．三、解答题（本大题共8个小题，满分56分）
-
17. 用适当的方法解方程：x（1﹣x）＝2x﹣2．18. 已知二次函数图象的顶点坐标为（1，﹣1），且经过原点（0，0），求该函数的解析式．19. 如图，△ABC内接于⊙O ， ∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D ， 若⊙O的半径为2，求CD的长．
20. 我县某楼盘准备以每平方米4000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．(1)、求平均每次下调的百分率．(2)、某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米50元，试问哪种方案更优惠？21. 如图，抛物线y＝ax2+2x+c经过点A（0，3），B（﹣1，0），请解答下列问题：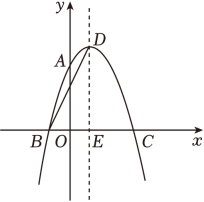
(1)、求抛物线的解析式；(2)、抛物线的顶点为点D ， 对称轴与x轴交于点E ， 连接BD ， 求BD的长．22. 如图，在△ABC中，∠B＝90°，AB＝6厘米，BC＝8厘米．点P从A点开始沿AB边向点B以1厘米/秒的速度移动（到达点B即停止运动），点Q从B点开始沿BC边向点C以2厘米/秒的速度移动（到达点C即停止运动）．
(1)、如果P、Q分别从A、B两点同时出发，经过几秒钟，△PBQ的面积等于△ABC的三分之一？(2)、如果P、Q两点分别从A、B两点同时出发，而且动点P从A点出发，沿AB移动（到达点B即停止运动），动点Q从B出发，沿BC移动（到达点C即停止运动），几秒钟后，P、Q相距6厘米？
