2023-2024学年高中数学人教A版必修二 10.3 频率与概率 同步练习
试卷更新日期:2023-12-16 类型:同步测试
一、选择题
-
1. 关于圆周率 , 数学史上出现过很多有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,可通过设计如下实验来估计值:先请100名同学每人随机写下一组正实数对 , 且要求 , 均小于1;再统计、和1作为三边长能形成钝角三角形的数对的个数;最后利用统计结果估计值.假如某次实验结果得到 , 那么本次实验可以将值估计为( )A、 B、 C、 D、2. 现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2、3表示没有击中目标, 4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数,根据以下数据估计该射击运动员射击4次至少击中3次的概率为( )
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
A、0.4 B、0.45 C、0.5 D、0.553. 已知P是△ABC所在平面内﹣点, ,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )A、 B、 C、 D、4. 从区间[0,1]内随机抽取2n个数 , ,… , ,.. , 构成n个数对( , ),…,( , ),其中两数的平方和不小于1的数对共有m个,则用随机模拟的方法得到圆周率π的近似值为( )A、 B、 C、 D、5. 为了了解奥运五环及其内部所占面积与单独五个圆环及其内部面积之和的比值P , 某同学设计了如右图所示的数学模型,通过随机模拟的方法,在长为8,宽为5的矩形内随机取了 个点,经统计落入五环及其内部的点的个数为 ,若圆环的半径为1,则比值 的近似值为( ) A、 B、 C、 D、6. 哈六中数学兴趣小组的同学们为了计算六中数学组二维码中黑色部分的面积,在如图一个边长为 的正方形区域内随机投掷 个点,其中落入黑色部分的有 个点,据此可估计黑色部分的面积为( )
A、 B、 C、 D、6. 哈六中数学兴趣小组的同学们为了计算六中数学组二维码中黑色部分的面积,在如图一个边长为 的正方形区域内随机投掷 个点,其中落入黑色部分的有 个点,据此可估计黑色部分的面积为( ) A、
A、 B、
C、
B、
C、 D、
D、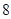 7. 如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为( )
7. 如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为( )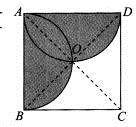 A、
A、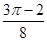 B、
B、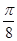 C、
C、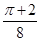 D、
D、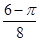 8. 关于圆周率 ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计 的值:先请120名同学每人随机写下一个 都小于1的正实数对 ,再统计其中 能与1构成钝角三角形三边的数对 的个数m,最后根据统计个数m估计 的值.如果统计结果是 ,那么可以估计 的值为( )
8. 关于圆周率 ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计 的值:先请120名同学每人随机写下一个 都小于1的正实数对 ,再统计其中 能与1构成钝角三角形三边的数对 的个数m,最后根据统计个数m估计 的值.如果统计结果是 ,那么可以估计 的值为( )
A、 B、 C、 D、9. 通过模拟试验,产生了20组随机数7130 3013 7055 7430 7740
4122 7884 2604 3346 0952
6107 9706 5774 5725 6576
5929 1768 6071 9138 6254
每组随机数中,如果恰有三个数在1,2,3,4,5,6中,则表示恰有三次击中目标,问四次射击中恰有三次击中目标的概率约为( )
A、 B、 C、 D、10. 《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是( )A、 B、 C、 D、二、填空题
-
11. 如图,在平放的边长为1的正方形中随机撒1000粒豆子,有380粒落到红心阴影部分上,据此估计红心阴影部分的面积为 .
 12. 如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为平方米.(用分数作答)
12. 如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为平方米.(用分数作答) 13. 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为 .
13. 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为 .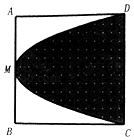 14. 关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请200名同学,每人随机写下一个都小于1 的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计π的值.假如统计结果是m=56,那么可以估计π≈ . (用分数表示)15. 已知单位圆内有一封闭图形,现向单位圆内随机撒N颗黄豆,恰有n颗落在该封闭图形内,则该封闭图形的面积估计值为 .16. 已知△ABC是一个面积较大的三角形,点P是△ABC所在平面内一点且 + +2 = ,现将3000粒黄豆随机抛在△ABC内,则落在△PBC内的黄豆数大约是 .17. 由计算机产生2n个0~1之间的均匀随机数x1 , x2 , …xn , y1 , y2 , …yn , 构成n个数对(x1 , y1),(x2y2),…(xn , yn)其中两数能与1构成钝角三角形三边的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为 .18. 如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为360颗,以此实验数据1000为依据可以估计出该不规则图形的面积为平方米.(用分数作答)
14. 关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请200名同学,每人随机写下一个都小于1 的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计π的值.假如统计结果是m=56,那么可以估计π≈ . (用分数表示)15. 已知单位圆内有一封闭图形,现向单位圆内随机撒N颗黄豆,恰有n颗落在该封闭图形内,则该封闭图形的面积估计值为 .16. 已知△ABC是一个面积较大的三角形,点P是△ABC所在平面内一点且 + +2 = ,现将3000粒黄豆随机抛在△ABC内,则落在△PBC内的黄豆数大约是 .17. 由计算机产生2n个0~1之间的均匀随机数x1 , x2 , …xn , y1 , y2 , …yn , 构成n个数对(x1 , y1),(x2y2),…(xn , yn)其中两数能与1构成钝角三角形三边的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为 .18. 如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为360颗,以此实验数据1000为依据可以估计出该不规则图形的面积为平方米.(用分数作答)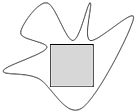
三、解答题
-
19. 解答题(1)、在边长为1的正方形ABCD内任取一点M,求事件“|AM|≤1”的概率;(2)、某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数x、y,统计出两数能与1构成锐角三角形的三边长的数对(x,y)共有12对,请据此估计π的近似值(精确到0.001).20. 设O为坐标原点,点P的坐标(x﹣2,x﹣y)(1)、在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;(2)、若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.21. 近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
厨余垃圾
400
100
100
可回收物
30
240
30
其他垃圾
20
20
60
(1)、试估计厨余垃圾投放正确的概率;(2)、试估计生活垃圾投放错误的概率;(3)、假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.(求:S2= [ + +…+ ],其中 为数据x1 , x2 , …,xn的平均数)
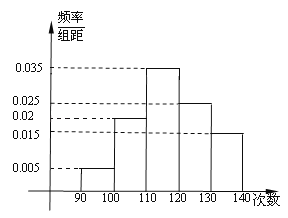
22.为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题:
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?