2023-2024学年高中数学人教A版必修二 10.1 随机事件与概率同步练习

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 下列关于概率的命题，错误的是（）

A、对于任意事件A ，都有 $P (A) \geq 0$ B、必然事件的概率为1 C、如果事件A与事件B对立，那么一定有 $P (A) + P (B) = 1$ D、若A ， B是一个随机试验中的两个事件，则 $P (A ∪ B) = P (A) + P (B)$

查看试题解析
2. 有一个人在打靶中，连续射击2次，事件“至少有1次中靶”的对立事件是（　　）

A、至多有1次中靶 B、2次都中靶 C、2次都不中靶 D、只有1次中靶

查看试题解析
3. 已知事件A与B互斥，且 $P (A) = 0.4$ ， $P (B) = 0.5$ ，则（）

A、 $P (A B) = 0.2$ B、 $P (A ∪ B) = 0.9$ C、 $P (\bar{A}) = 0.5$ D、 $P (\bar{B}) = 0.6$

查看试题解析
4. 某运动员射击一次所得环数的分布列如表所示，则 $P (ξ \geq 9) =$ （）

$ξ$

8

9

10

P

0.36

a

0.33

A、0.64 B、0.66 C、0.67 D、0.69

查看试题解析
5. 已知事件 $A$ 与事件 $B$ 是互斥事件，则（）

A、 $P (\bar{A} \cap \bar{B}) = 0$ B、 $P (A \cap B) = P (A) P (B)$ C、 $P (A) = 1 - P (B)$ D、 $P (\bar{A} \cup \bar{B}) = 1$

查看试题解析
6. 某饮料生产企业推出了一种有一定几率中奖的新饮料．甲､乙两名同学都购买了这种饮料，设事件 $A$ 为“甲､乙都中奖”，则与 $A$ 互为对立事件的是（）

A、甲､乙恰有一人中奖 B、甲､乙都没中奖 C、甲､乙至少有一人中奖 D、甲､乙至多有一人中奖

查看试题解析
7. 在一个盒子中有红球和黄球共5个球，从中不放回的依次摸出两个球，事件 $A =$ “第二次摸出的球是红球”，事件 $B =$ “两次摸出的球颜色相同”，事件 $C =$ “第二次摸出的球是黄球”，若 $P (A) = \frac{2}{5}$ ，则下列结论中错误的是（）

A、 $P (B) = \frac{2}{5}$ B、 $P (C) = 1 - P (A)$ C、 $P (A \cup^{} B) = \frac{4}{5}$ D、 $P (A \cap^{} B) = \frac{1}{10}$

查看试题解析
8. 把红、黑、蓝、白4张纸牌随机地发给甲、乙、丙、丁4个人，每人分得 $1$ 张，事件“甲分得红牌”与事件“乙分得红牌”是（）

A、对立事件 B、不可能事件 C、互斥事件但不是对立事件 D、以上答案都不对

查看试题解析
9. 甲盒中有200个螺杆，其中有 $x$ 个 $A$ 型的，乙盒中有240个螺母，其中有 $y$ 个 $A$ 型的．今从甲、乙两盒中各任取一个，不能配成 $A$ 型螺栓的概率为 $\frac{2}{5}$ ，则恰好可配成 $A$ 型螺栓的概率为（）

A、 $\frac{1}{20}$ B、 $\frac{15}{16}$ C、 $\frac{3}{5}$ D、 $\frac{19}{20}$

查看试题解析
10. 从 1，2，3，4，5 这5个数中任取两个数，其中：①恰有一个是偶数和恰有一个是奇数；②至少有一个是奇数和两个都是奇数；③至少有一个是奇数和两个都是偶数；④至少有一个是奇数和至少有一个是偶数，上述事件中，是对立事件的是（）

A、① B、②④ C、③ D、①③

查看试题解析
11. 对于任意事件 $M$ 和 $N$ ，有（）

A、 $P (M \cup^{} N) = P (M) + P (N)$ B、 $P (M \cup^{} N) > P (M) + P (N)$ C、 $P (M \cup^{} N) < P (M) + P (N)$ D、 $P (M \cup^{} N) \leq P (M) + P (N)$

查看试题解析
12. 从装有5个红球和3个白球的口袋内任取3个球，那么下列各对事件中，互斥而不对立的是（）

A、恰有一个红球与恰有两个红球 B、至少有一个红球与都是白球 C、至少有一个红球与至少有个白球 D、至少有一个红球与都是红球

查看试题解析

二、多项选择题

13. 下列四个命题中，假命题有（）

A、对立事件一定是互斥事件 B、若A ， B为两个事件，则 $P (A ∪ B) = P (A) + P (B)$ C、若事件A ， B ， C彼此互斥，则 $P (A) + P (B) + P (C) = 1$ D、若事件A ， B满足 $P (A) + P (B) = 1$ ，则A ， B是对立事件

查看试题解析
14. 中国篮球职业联赛（CBA）中，某运动员在最近几次比赛中的得分情况如下表：
投篮次数
投中两分球的次数
投中三分球的次数
100
65
16
记该运动员在一次投篮中，投中两分球为事件A，投中三分球为事件B，没投中为事件C，且事件A，B，C是否发生互不影响，用频率估计事件A，B，C发生的概率 $P (A)$ ， $P (B)$ ， $P (C)$ ，下述结论中正确的是（）

A、 $P (A) = 0.65$ B、 $P (B) = 0.16$ C、 $P (C) = 0.19$ D、 $P (B + C) = 0.65$

查看试题解析
15. 中国篮球职业联塞（CBA）中，某男篮球运动是在最近几次比赛中的得分情况如下表：
投篮次数
投中两分球的次数
投中三分球的次数
没投中
100
55
18
m
记该运动员在一次投篮中，投中两分球为事件A，投中三分球为事件B，没投中为事件C，用频率估计概率的方法，得到的下述结论中，正确的是（）

A、 $P (A) = 0.55$ B、 $P (A + B) = 0.73$ C、 $P (C) = 0.27$ D、 $P (B + C) = 0.55$

查看试题解析
16. 某小组有2名男生和3名女生，从中任选2名同学去参加唱歌比赛，在下列各组事件中，是互斥事件的是（）

A、恰有1名女生和恰有2名女生 B、至少有1名男生和至少有1名女生 C、至少有1名女生和全是女生 D、至少有1名女生和全是男生

查看试题解析
17. 某校高一年级开设了甲､乙两个课外兴趣班，供学生们选择，记事件 $Ω_{1} =$ “只选择甲兴趣班"， $Ω_{2}$ =“至少选择一个兴趣班”， $Ω_{3}$ =“至多选择一个兴趣班”， $Ω_{4} =$ “一个兴趣班都不选”，则（）

A、 $Ω_{1}$ 与 $Ω_{3}$ 是互斥事件 B、 $Ω_{2}$ 与 $Ω_{4}$ 既是互斥事件也是对立事件 C、 $Ω_{2}$ 与 $Ω_{3}$ 不是互斥事件 D、 $Ω_{3}$ 与 $Ω_{4}$ 是互斥事件

查看试题解析
18. 从装有3个红球和2个白球的袋中任意取出2个球，有如下几对事件：
①“取出2个球，恰好有1个白球”与“取出2个球，恰好有1个红球”；②“取出2个球，恰好有1个白球”与“取出2个球，都是红球”；③“取出2个球，至少有1个白球”与“取出2个球，都是红球”；④“取出2个球，至少有1个白球”与“取出2个球，至少有1个红球”．其中是互斥事件的有（）

A、① B、② C、③ D、④

查看试题解析

三、填空题

19. 如图所示，靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成，射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35、0.30、0.25，则不命中靶的概率是.

查看试题解析
20. 已知事件A与事件B互斥，如果 $P (A) = 0.3$ ， $P (B) = 0.5$ ，那么 $P (\bar{A ∪ B}) =$ ．

查看试题解析
21. 安排 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 五名志愿者到甲，乙两个福利院做服务工作，每个福利院至少安排一名志愿者，则 $A$ ， $B$ 被安排在不同的福利院的概率为．

查看试题解析
22. 已知事件 $A$ 、 $B$ 互斥， $P (A ∪ B) = \frac{3}{5}$ ，且 $P (A) = 2 P (B)$ ，则 $P (\bar{B}) =$ .

查看试题解析
23. 现有分别写有数字2至8的7张卡片，将写有质数的卡片放入A箱中，将写有合数的卡片放入B箱中，从A箱中随机抽取一张卡片放入B箱中，再从B箱中随机抽取两张卡片，抽取的两张卡片上的数字互质的概率为．

查看试题解析
24. 已知甲盒装有3个红球， $m$ 个白球，乙盒装有3个红球， 1个白球，丙盒装有2个红球， 2个白球，这些球除颜色以外完全相同. 先随机取一个盒子，再从该盒子中随机取一个球，若取得白球的概率是 $\frac{37}{84}$ ，则 $m =$ .

查看试题解析

四、解答题

25. 现有A，B两个广西旅行社，统计了这两个旅行社的游客去漓江、乐满地主题乐园、西街、龙脊梯田四个景点旅游的各240人次的数据，并分别绘制出这两个旅行社240人次分布的柱形图，如图所示．假设去漓江、乐满地主题乐园、西街、龙脊梯田旅游每人次的平均消费分别为1200元、1000元、600元、200元．

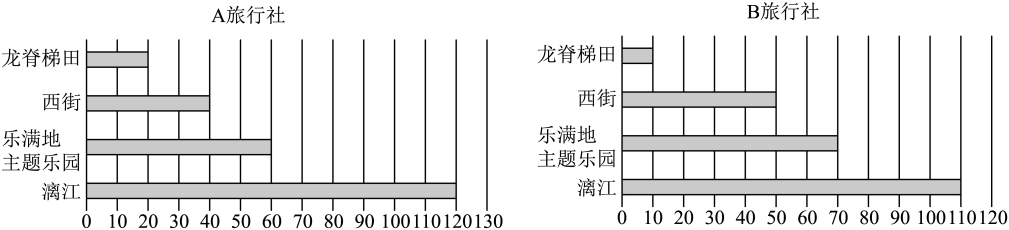(1)、通过计算，比较这两个旅行社240人次的消费总额哪个更大；

(2)、若甲和乙分别去A旅行社、B旅行社，并都从这四个景点中选择一个去旅游，以这240人次去漓江的频率为概率，求甲、乙至少有一人去漓江的概率．

查看试题解析
26. 袋中有9个大小相同颜色不全相同的小球，分别为黑球､黄球､绿球，从中任意取一球，得到黑球或黄球的概率是 $\frac{5}{9}$ ，得到黄球或绿球的概率是 $\frac{2}{3}$ ，试求：

(1)、从中任取一球，得到黑球､黄球､绿球的概率各是多少？

(2)、从中任取两个球，得到的两个球颜色不相同的概率是多少？

查看试题解析
27. 某次联欢会上设有一个抽奖游戏抽奖箱中共有16个四种不同颜色且形状大小完全相同的小球，分别代表－等奖、二等奖、三等奖、无奖四种奖项．其中红球代表一等奖且只有1个，黄球代表三等奖．从中任取一个小球，若中二等奖或三等奖的概率为 $\frac{7}{16}$ ，小华同学获得一次摸奖机会．

(1)、求他不能中奖的概率；

(2)、若该同学中一等奖或二等奖的概率是 $\frac{1}{4}$ ，试计算黄球的个数．

查看试题解析
28. 某中学根据学生的兴趣爱好，分别创建了“书法”、“诗词”、“理学”三个社团，据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学，假设他通过考核选拔进入该校的“书法”、“诗词”、“理学”三个社团的概率依次为 $m$ 、 $\frac{1}{3}$ 、 $n$ ，已知三个社团他都能进入的概率为 $\frac{1}{24}$ ，至少进入一个社团的概率为 $\frac{3}{4}$ ，且 $m > n$ .

(1)、求 $m$ 与 $n$ 的值；

(2)、该校根据三个社团活动安排情况，对进入“书法”社的同学增加校本选修学分1分，对进入“诗词”社的同学增加校本选修学分2分，对进入“理学”社的同学增加校本选修学分3分．求该新同学在社团方面获得校本选修课学分分数不低于4分的概率．

查看试题解析

投篮次数	投中两分球的次数	投中三分球的次数
100	65	16

$ξ$	8	9	10
P	0.36	a	0.33

2023-2024学年高中数学人教A版必修二 10.1 随机事件与概率 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版必修二 10.1 随机事件与概率同步练习