2023-2024学年高中数学人教A版必修二 9.3 统计分析 同步练习

试卷更新日期：2023-12-16 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 某学校有男生600人，女生400人．为调查该校全体学生每天的运动时间，采用分层抽样的方法获取容量为n的样本．经过计算，样本中男生每天运动时间的平均值为80分钟，方差为10；女生每天运动时间的平均值为60分钟，方差为20．结合数据，估计全校学生每天运动时间的方差为（ ）
    A、96 B、110 C、112 D、128

    查看试题解析

  • 2. 某校为了了解学生的身体素质，对2022届初三年级所有学生仰卧起坐一分钟的个数情况进行了数据统计，结果如下图所示.该校2023届初三学生人数较2022届初三学生人数上升了10%，则下列说法错误的是（ ）

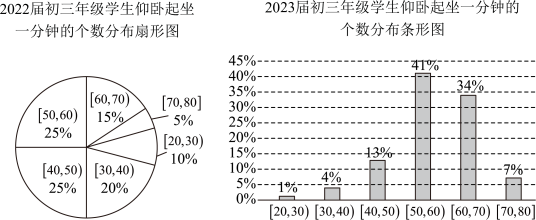    A、该校2022届初三年级学生仰卧起坐一分钟的个数在[30 ， 60)内的学生人数占70% B、该校2023届初三学生仰卧起坐一分钟的个数在[60 ， 80]内的学生人数比2022届初三学生仰卧起坐一分钟个数同个数段的学生人数的2倍还多 C、该校2023届初三学生仰卧起坐一分钟的个数和2022届初三学生仰卧起坐一分钟个数的中位数均在[50 ， 60)内 D、相比2022届初三学生仰卧起坐一分钟个数不小于50的人数，2023届初三学生仰卧起坐一分钟个数不小于50的人数占比增加

    查看试题解析

  • 3. 某高中共有学生2400人，其中高一、高二、高三的学生人数比为5∶4∶6，现用分层随机抽样的方法从该高中所有学生中抽取一个容量为120的样本，则应从高三年级抽取的人数为（ ）
    A、32 B、40 C、48 D、56

    查看试题解析

  • 4. 某校通过统计学生在校的5次模考数学成绩（分数均为整数）决定该学生是否适合进行数学竞赛培训．规定：“5次模考成绩均不低于140分”，现有甲、乙、丙三位同学5次模考成绩，则根据以下数据能确定适合数学竞赛培训的学生有（    ）

    甲：众数为140，中位数为145；

    乙：中位数为145，极差为6；

    丙：均值为143，其中一次成绩为145，方差为1.6．

    A、甲乙 B、甲丙 C、乙丙 D、甲乙丙

    查看试题解析

  • 5. 已知某班40名学生某次考试的数学成绩依次为x1 ， x2 ， x3 ， ⋅⋅⋅ ， x40 ， 经计算全班数学平均成绩x¯=90 ， 且∑i=140xi2=324400 ， 则该班学生此次数学成绩的标准差为（    ）
    A、20 B、25 C、10 D、10

    查看试题解析

  • 6. 为了解学生的课外阅读情况，某校对高中生进行平均每周课外阅读时间（单位：小时）的调查，采用样本量比例分配的分层随机抽样.如果不知道样本数据，只知道抽取了男生40人，其平均数和方差分别为5和1.65，抽取了女生60人，其平均数和方差分别为4和3.5，则估计该校学生平均每周课外阅读时间的总体方差为（    ）
    A、2.58 B、2.76 C、3 D、3.2

    查看试题解析

  • 7. 四名同学各掷骰子5次，分别记录每次骰子出现的点数.根据四名同学的统计结果，可以判断出一定没有出现点数6的是（    ）
    A、中位数为3，众数为3 B、中位数为3，极差为3 C、平均数为3，中位数为3 D、平均数为3，众数为4

    查看试题解析

  • 8. 水果收购商为了了解某种水果的品质，想用分层抽样的方法从500个大果，300个中果，200个小果中抽取一部分送去质检部门检验，若抽取的小果为30个，则他抽取的大果为（ ）个.
    A、150 B、75 C、45 D、15

    查看试题解析

  • 9. 在某地区某高传染性病毒流行期间，为了建立指标显示疫情已受控制，以便向该地区居众显示可以过正常生活，有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”，根据连续7天的新增病例数计算，下列① ~ ⑤各个选项中，一定符合上述指标的是 (    )
    ①平均数x_≤3； ②标准差S≤2； ③平均数x_≤3且标准差S≤2；
    ④平均数x_≤3且极差小于或等于2；⑤众数等于1且极差小于或等于4。

    A、①② B、③④ C、③④⑤ D、④⑤

    查看试题解析

  • 10. 从甲、乙两班分别任意抽出10名学生进行英语口语测验，其测验成绩的方差分别为S12= 13.2，S22=26.26，则

    A、甲班10名学生的成绩比乙班10名学生的成绩整齐 B、乙班10名学生的成绩比甲班10名学生的成绩整齐 C、甲、乙两班10名学生的成绩一样整齐 D、不能比较甲、乙两班10名学生成绩的整齐程度

    查看试题解析

二、多项选择题

  • 11. 下列说法正确的是（ ）
    A、抽样调查具有花费少、效率高的特点 B、数据2 ， 3 ， 9 ， 5 ， 3 ， 9的中位数为7 ， 众数为3和9 C、极差和标准差都能描述一组数据的离散程度 D、数据a1 ， a2 ， ⋅⋅⋅ ， an的方差为s2 ， 则数据2a1 ， 2a2 ， ⋅⋅⋅ ， 2an的方差为2s2

    查看试题解析

  • 12. 有一组样本数据x1 ， x2 ， ⋅⋅⋅xn ， 另一组样本数据y1 ， y2 ， ⋅⋅⋅yn ， 其中yi=xi−2c(i=1 ， 2 ， ⋅⋅⋅n) ， c为非零常数，则（  ）
    A、两组样本数据平均数相同 B、两组样本数据方差相同 C、两组样本数据中位数相等 D、两组样本数据极差相同

    查看试题解析

  • 13. 近年来､新冠疫情波及到千家万户，人们的生活方式和习惯不得不发生转变，短视频成了观众空闲时娱乐活动的首选．某电影艺术中心为了解短视频平台的观众年龄分布情况，向各大短视频平台的观众发放了线上调查问卷，共回收有效样本4000份，根据所得信息制作了如图所示的频率分布直方图，则下列说法正确的是（   ）

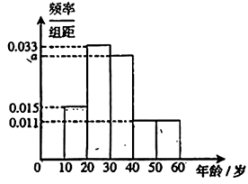    A、图中a=0.028 B、在4000份有效样本中，短视频观众年龄在10~20岁的有1320人 C、估计短视频观众的平均年龄为32岁 D、估计短视频观众年龄的75%分位数为39岁

    查看试题解析

  • 14. 下列说法正确的是（ ）
    A、数据1，2，3，3，4，5的平均数和中位数相同 B、数据6，5，4，3，3，3，2，2，1的众数为3 C、有甲、乙、丙三种个体按3：1：2的比例分层抽样调查，如果抽取的甲个体数为9，则样本容量为30 D、甲组数据的方差为4，乙组数据为5，6，9，10，5，则这两组数据中较稳定的是乙组

    查看试题解析

  • 15. 为了向社会输送优秀毕业生，中等职业学校越来越重视学生的实际操作（简称实操）能力的培养．中职生小王在对口工厂完成实操产品100件，质检人员测量其质量（单位：克），将所得数据分成5组：[95 ， 97) ， [97 ， 99) ， [99 ， 101) ， [101 ， 10) ， [103 ， 105] ． 根据所得数据制成如图所示的频率分布直方图，其中质量在[99 ， 101)内的为优等品．对于这100件产品，下列说法正确的是（ ）

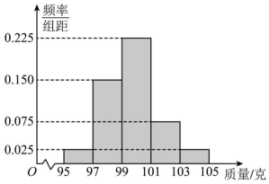    A、质量的平均数为99.7克（同一区间的平均数用区间中点值代替） B、优等品有45件 C、质量的众数在区间[98 ， 100)内 D、质量的中位数在区间[99 ， 101)内

    查看试题解析

  • 16. 已知一组数据x1 ， x2 ， ⋯ ， xn的平均数为a ， 中位数为b ， 方差为c ， 众数为d ， 数据−2x1+1 ， −2x2+1 ， ⋯ ， −2xn+1的平均数为a1 ， 中位数为b1 ， 方差为c1 ， 众数为d1 ， 则（    ）
    A、a1=−2a+1 B、b1无法确定 C、c1=−2c+1 D、d1=−2d+1

    查看试题解析

三、填空题

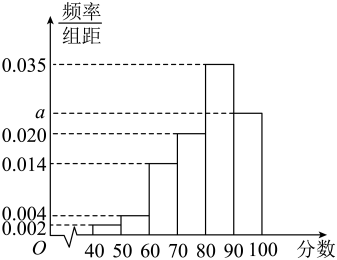
  • 17. 已知一组样本数据x1 ， x2 ， x3 ， x4 ， x5的方差为5，且满足x1+x2+x3+x4=4x5 ， 则样本数据x1 ， x2 ， x3 ， x4 ， x5+5的方差为.

    查看试题解析

  • 18.  湖州地区甲、乙、丙三所学科基地学校的数学强基小组人数之比为3：2：1 ， 三所学校共有数学强基学生48人，在一次统一考试中，所有学生的成绩平均分为117，方差为21.5．已知甲、乙两所学校的数学强基小组学生的平均分分别为118和114，方差分别为15和21，则丙学校的学生成绩的方差是.

    查看试题解析

  • 19. 为迎接2023年成都大运会，大运会组委会采用按性别分层抽样的方法从200名大学生志愿者中抽取30人组成大运会志愿小组.若30人中共有男生12人，则这200名学生志愿者中女生可能有人.

    查看试题解析

  • 20. 一组数据由8个数组成，将其中一个数由4改为2，另一个数由6改为8，其余数不变，得到新的一组数据，则新的一组数的方差相比原一组数的方差的增加值为 ．

    查看试题解析

  • 21. 某校为了了解高三年级学生的身体素质状况，在开学初举行了一场身体素质体能测试，以便对体能不达标的学生进行有针对性的训练，促进他们体能的提升，现从整个年级测试成绩中抽取100名学生的测试成绩，并把测试成绩分成[40 ， 50) ， [50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100]六组，绘制成频率分布直方图（如图所示）.其中分数在[90 ， 100]这一组中的纵坐标为a ， 则该次体能测试成绩的80%分位数约为分.

    查看试题解析

  • 22. 某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[12.5 ， 25] ， 样本数据分组为[12.5 ， 15) ， [15 ， 17.5) ， [17.5 ， 20) ， [20 ， 22.5) ， [22.5 ， 25] ． 根据频率分布直方图，这200名学生中每周的自习时间不少于20小时的人数是 ．

    查看试题解析

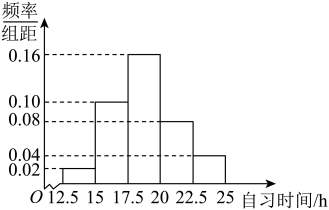  • 23. 近年来，加强青少年体育锻炼，重视体质健康已经在社会形成高度共识.2021年10月，《中华人民共和国体育法》在颁布20多年后迎来首次大修.教育部发布的2022年工作要点中提出，实施学校体育和体教融合改革发展行动计划.为了考察某校各班参加两项以上体育项目锻炼小组的人数，在全校随机抽取五个班级，把每个班级参加两项以上体育项目锻炼小组的人数作为样本数据.已知样本平均数为7，样本的标准差为2，若样本数据各不相同，则样本数据的第80百分位数是.

    查看试题解析

  • 24. 慢走是一种简单又优良的锻炼方式，它不仅可以帮助减肥，还可以增强心肺功能、血管弹性、肌肉力量等.小南计划近6个月的月慢走里程（单位：公里）按从小到大排列依次为11，12，m ， n ， 20，27，且这6个月的月慢走里程的中位数为16，若要使这6个月的月慢走里程的标准差最小，则m=.

    查看试题解析

四、解答题

  • 25. 某校对参加亚运知识竞赛的100名学生的成绩进行统计，分成[50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100]五组，得到如图所示频率分布直方图．

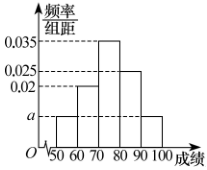    (1)、估计该校参加亚运知识竞赛的学生成绩的众数和平均数；
    (2)、估计该校参加亚运知识竞赛的学生成绩的80%分位数．

    查看试题解析

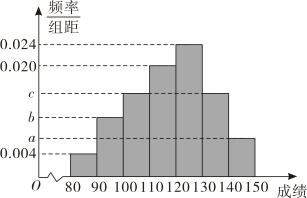  • 26. 某校高三年级甲班50名学生在一次期中考试中，数学成绩的频率分布直方图如图所示，成绩分组区间为[80 ， 90) ， [90 ， 100) ， [100 ， 110) ， [110 ， 120) ， [120 ， 130) ， [130 ， 140) ， [140 ， 150].其中a+c=2b ， 且c=2a ．

    (1)、根据甲班数学成绩的频率分布直方图，估计甲班数学成绩的平均分；
    (2)、求数学成绩的第80百分位数．

    查看试题解析

  • 27. 某工厂生产某款产品，该产品市场评级规定：评分在10分及以上的为一等品，低于10分的为二等品．下面是检验员从一批产品中随机抽取的10件产品的评分：  

    9.6

    10.1

    9.7

    9.8

    10.0

    9.7

    10.0

    9.8

    10.1

    10.2

    经计算得110∑i=110xi2≈98.048 ， 其中xi为抽取的第i件产品的评分，i=1 ， 2 ， 3 ， ⋅⋅⋅ ， 10 ．

    (1)、求这组样本平均数和方差；
    (2)、若厂家改进生产线，使得生产出的每件产品评分均提高0.2．根据以上随机抽取的10件产品改进后的评分，估计改进后该厂生产的产品评分的平均数和方差；
    (3)、在第（2）问前提下，再从改进后生产的产品中随机抽取的10件产品，估计这10件产品平均等级是否为一等品？说明理由．

    查看试题解析

  • 28. 小晟统计了他6月份的手机通话明细清单，发现自己该月共通话100次，小晟将这100次通话的通话时间（单位：分钟）按照(0 ， 4) ， [4 ， 8) ， [8 ， 12) ， [12 ， 16) ， [16 ， 20) ， [20 ， 24]分成6组，画出的频率分布直方图如图所示．

    (1)、求a的值；
    (2)、求通话时间在区间[4 ， 12)内的通话次数；
    (3)、试估计小晟这100次通话的平均时间（同一组中的数据用该组区间的中点值作代表）．

    查看试题解析

  • 29.  4月23日是世界读书日，又称“世界图书日”.今年是安徽省开展全民阅读活动的第十年，某市组织学生参加“书香安徽·皖美阅读”活动.为了解该市义务教育阶段学生每周读书时间，按小学生和初中生进行分层，采用比例分配的分层随机抽样方法抽取了样本量为1000的样本进行调查，其中小学生600人，初中生400人，发现他们的每周读书时间都在200～500分钟之间，进行适当分组后(每组都是左闭右开的区间)，画出频率分布直方图如图所示.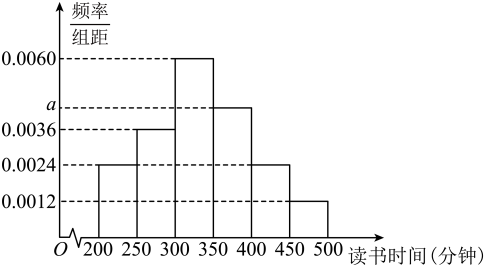

    (1)、求a的值；
    (2)、若上述样本中小学生每周读书时间的平均数为320分钟，请根据频率分布直方图估计样本中初中生每周读书时间的平均数.

    查看试题解析

  • 30. 某公司最近10年的盈利依次记为x1 ， x2 ， …，x10（单位：万元），x¯ ， S2分别表示平均值与方差.
    (1)、若x1=x4=x7=x10=8 ， x2=x5=x8=7 ， x3=x6=x9=9 ， 求x¯ ， S2的值；
    (2)、若x¯=9 ， S2=0.5 ， 求xi2(i=1 ， 2 ， ⋯ ， 10)的平均值.

    查看试题解析

  • 31. 某大型企业为员工谋福利，与某手机通讯商合作，为员工办理流量套餐.为了解该企业员工手机流量使用情况，通过抽样，得到100名员工近一周每人手机日平均使用流量L（单位：M）的数据，其频率分布直方图如图：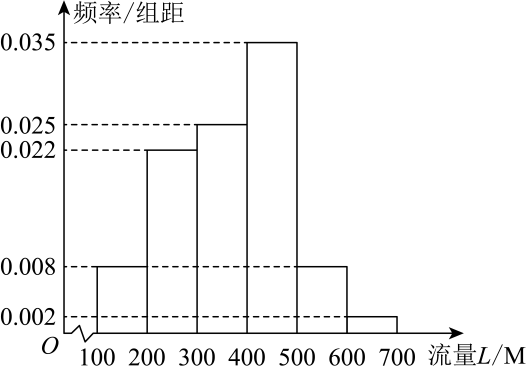

      

    若将每位员工的手机日平均使用流量分别视为其手机日使用流量，回答以下问题.

    (1)、求这100名员工近一周每人手机日使用流量的众数、中位数；
    (2)、在办理流量套餐后，采用样本量比例分配的分层随机抽样，如果不知道样本数据，只知道抽取了男员工20名，其手机日使用流量的平均数为800M，方差为10000；抽取了女员工40名，其手机日使用流量的平均数为1100M，方差为40000.

    （i）已知总体划分为2层，通过分层随机抽样，各层抽取的样本量、样本平均数和样本方差分别为：m ， x¯ ， s12；n ， y¯ ， s22 ， 记总的样本平均数为ω¯ ， 样本方差为s2.证明：s2=1m+n{m[s12+(x¯−ω¯)2]+n[s22+(y¯−ω¯)2]}.

    （ii）用样本估计总体，试估计该大型企业全体员工手机日使用流量的平均数和方差.

    查看试题解析

  • 32. 为了解某市今年高一年级学生的身体素质状况，从该市高一年级学生中抽取100名学生进行“掷实心球”的项目测试.经统计，成绩均在2米到12米之间，把获得的所有数据分[2 ， 4) ， [4 ， 6) ， [6 ， 8) ， [8 ， 10) ， [10 ， 12)成五组，得到频率分布直方图如图所示.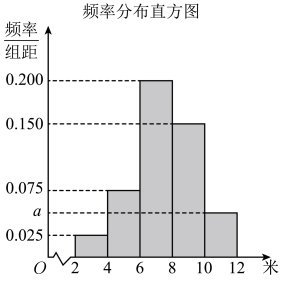

    (1)、根据频率分布直方图，估计该市今年高一年级学生“掷实心球”成绩的平均数（同一组中的数据以该组区间的中点值作代表）；
    (2)、已知这100名学生中有女生40名，男生60名，这40名女生“掷实心球”成绩的平均数和方差分别为7和2.1，这60名男生“掷实心球”成绩的平均数和方差分别为8.5和2.4，求这100名学生“掷实心球”成绩的方差.

    查看试题解析