2023-2024学年高中数学人教A版必修二 9.2 用样本估计总体同步练习

试卷更新日期：2023-12-16 类型：同步测试

进入出卷网下载

一、选择题

1. 2023年“三月三”期间，广西交通部门统计了2023年4月19日至4月25日的高速公路车流量（单位：万车次），并与2022年比较，得到同比增长率（同比增长率＝（今年车流量-去年同期车流量）÷去年同期车流量×100％））数据，绘制了如图所示的统计图，则下列结论错误的是（）

A、2023年4月19日至4月25日的高速公路车流量的极差为23 B、2023年4月19日至4月25日的高速公路车流量的中位数为17 C、2023年4月19日至4月21日的高速公路车流量的标准差小于2023年4月23日至4月25日的高速公路车流量的标准差 D、2022年4月23日的高速公路车流量为20万车次

查看试题解析
2. 已知样本数据 $x_{1}$ ， $x_{2}$ ， …， $x_{2022}$ 的平均数和方差分别为3和56，若 $y_{i} = 2 x_{i} + 3 (i = 1 ， 2 ， ⋯ ， 2022)$ ，则 $y_{1}$ ， $y_{2}$ ， … $y_{2022}$ 的平均数和方差分别是（）

A、12，115 B、12，224 C、9，115 D、9，224

查看试题解析
3. 某中学举行了一次“网络信息安全”知识竞赛，将参赛的100名学生成绩分为6组，绘制了如图所示的频率分布直方图，则成绩在区间 $[75 ， 80)$ 内的学生有（）

A、15名 B、20名 C、25名 D、40名

查看试题解析
4. 某校为了解学生体能素质，随机抽取了100名学生进行体能测试，并将这100名学生成绩整理得如下频率分布直方图.根据此频率分布直方图，下列结论中正确的是（）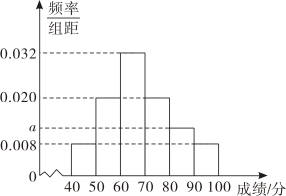

A、图中a＝0.12 B、这100名学生中成绩在[50，70）内的人数为50 C、这100名学生成绩的中位数为70 D、这100名学生的平均成绩为68.2（同一组中的数据用该组区间的中点值做代表）

查看试题解析
5. 若一组样本数据 $x_{1}$ ， $x_{2}$ ， …， $x_{n}$ 的方差为0.01，则数据 $4 x_{1} + 1$ ， $4 x_{2} + 1$ ， $4 x_{3} + 1$ ， …， $4 x_{n} + 1$ 的方差为（）

A、0.04 B、1.16 C、0.16 D、1.04

查看试题解析
6. “治国之道，富民为始.”共同富裕是社会主义的本质要求，是中国式现代化的重要特征，是人民群众的共同期盼.共同富裕是全体人民通过辛勤劳动和相互帮助最终达到丰衣足食的生活水平，是消除两极分化和贫穷基础上的普遍富裕.请你运用数学学习中所学的统计知识加以分析，下列关于个人收入的统计量中，最能体现共同富裕要求的是（）

A、平均数大，方差大 B、平均数大，方差小 C、平均数小，方差大 D、平均数小，方差小

查看试题解析

7. 甲、乙、丙、丁四人参加奥运会射击项目选拔赛，四人的平均成绩和方差如表所示：从这四个人中选择一人参加奥运会射击项目比赛，最佳人选是（）

	甲	乙	丙	丁
平均成绩 $\bar{x}$	8.6	8.9	8.9	8.2
方差 $s^{2}$	3.5	5.6	2.1	3.5

A、甲 B、乙 C、丙 D、丁

查看试题解析

8. 设样本数据 $x_{1}$ ， $x_{2}$ ， …， $x_{10}$ 的均值和方差分别为1和4，若 $y_{i} = 2 x_{i} + a$ ( $a$ 为非零常数， $i = 1 ， 2 ， \cdot \cdot \cdot ， 10$ )，则 $y_{1}$ ， $y_{2}$ ， …， $y_{10}$ 的均值和方差分别为（）

A、2，8 B、2， $8 + a$ C、 $2 + a$ ， 16 D、 $2 + a$ ， $16 + a$

查看试题解析
9. 现有一个容量为50的样本，其数据的频数分布表如下表所示：
组号
1
2
3
4
5
频数
8
11
10
$x$
9
则第4组的频数和频率分别是（）

A、12，0.06 B、12，0.24 C、18，0.09 D、18，0.36

查看试题解析
10. 为了学习、宣传和践行党的二十大精神，某班组织全班学生开展了以“学党史、知国情、圆梦想”为主题的党史暨时政知识竞赛活动．已知该班男生 $20$ 人，女生 $30$ 人，根据统计分析，男生组成绩和女生组成绩的方差分别为 $s_{1}^{2} ， s_{2}^{2}$ ．记该班成绩的方差为 $s^{2}$ ，则下列判断正确的是（）

A、 $s^{2} = \frac{s_{1}^{2} + s_{2}^{2}}{2}$ B、 $s^{2} \geq \frac{s_{1}^{2} + s_{2}^{2}}{2}$ C、 $s^{2} = \frac{2 s_{1}^{2} + 3 s_{2}^{2}}{5}$ D、 $s^{2} \geq \frac{2 s_{1}^{2} + 3 s_{2}^{2}}{5}$

查看试题解析
11. 已知样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{100}$ 的方差为4，若由 $y_{1} = 2 x_{1} + 3$ ， $y_{2} = 2 x_{2} + 3 ， ⋯$ ， $y_{100} = 2 x_{100} + 3$ 得到另一组样本数据 $y_{1} ， y_{2} ， ⋯ ， y_{100}$ ，则样本数据 $y_{1} ， y_{2} ， ⋯ ， y_{100}$ 的方差为（）

A、8 B、16 C、32 D、64

查看试题解析
12. 如图，一组数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …， $x_{9}$ ， $x_{10}$ 的平均数为5，方差为 $s_{1}^{2}$ ，去除 $x_{9}$ ， $x_{10}$ 这两个数据后，平均数为 $\bar{x}$ ，方差为 $s_{2}^{2}$ ，则（）

A、 $\bar{x} > 5$ ， $s_{1}^{2} > s_{2}^{2}$ B、 $\bar{x} < 5$ ， $s_{1}^{2} < s_{2}^{2}$ C、 $\bar{x} = 5$ ， $s_{1}^{2} < s_{2}^{2}$ D、 $\bar{x} = 5$ ， $s_{1}^{2} > s_{2}^{2}$

查看试题解析
13. 某校有年轻教师30人和老教师20人进行党史答题比赛．按照分层抽样的方法抽取5名教师，相关统计情况如下：年轻教师答对题目的平均数为2，方差为0.5；老教师答对题目的平均数为3，方差为1，则这5人答对题目的方差为（）

A、0.61 B、0.675 C、0.74 D、0.94

查看试题解析
14. 一组数据由6个数组成，将其中一个数由4改为6，另一个数由12改为10，其余数不变，得到新的一组数据，则新的一组数的方差减去原一组数的方差的差为（）

A、4 B、3 C、-4 D、-3

查看试题解析
15. 某学校随机抽取了部分学生，对他们每周使用手机的时间进行统计，得到如下的频率分布直方图.则下列说法：① $a = 0.03$ ；②若抽取100人，则平均用时13.75小时：③若从每周使用时间在 $[15 ， 20) ， [20 ， 25)$ ， $[25 ， 30)$ 三组内的学生中用分层抽样的方法选取8人进行访谈，则应从使用时间在 $[20 ， 25)$ 内的学生中选取的人数为3.其中正确的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
16. 某学校调查了高三1000名学生每周的自习时间(单位：小时)，制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为 $[17.5 ， 20) 、 [20 ， 22.5)$ 、 $[22.5 ， 25) 、 [25 ， 27.5) 、 [27.5 ， 30]$ .根据直方图，以下结论不正确的是（）

A、估计这1000名学生每周的自习时间的众数是23.85 B、估计这1000名学生每周的自习时间的中位数是23.75 C、估计这1000名学生每周的自习时间小于22.5小时的人数是300 D、估计这1000名学生每周的自习时间不小于25小时的人数是300

查看试题解析

二、多项选择题

17. 舟山某校为了加强食堂用餐质量，该校随机调查了100名学生，根据这100名学生对食堂用餐质量给出的评分数据，分成 $[50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100]$ 五组，得到如图所示的频率分布直方图，则下列结论正确的是（）

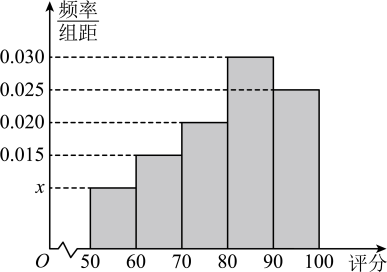A、 $x = 0.01$ B、该样本数据的中位数和众数均为85 C、若样本数据的平均数低于85分，则认为食堂需要整改，根据此样本我们认为该校食堂需要整改 D、为了解评分较低的原因，该校从评分低于80分的学生中用分层抽样的方法随机抽取18人座谈，则应选取评分在 $[50 ， 60)$ 的学生4人

查看试题解析
18. 如图为国家统计局公布的2017~2022年全国城镇居民人均可支配收入及人均消费支出统计图，则（）

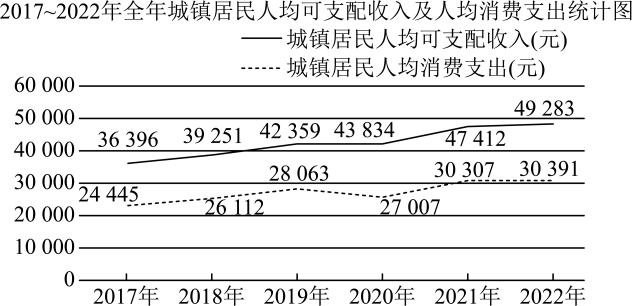A、2017~2022年全国城镇居民人均可支配收入及人均消费支出均呈增长趋势 B、2017~2022年全国城镇居民人均消费支出的中位数为27535 C、2017~2022年全国城镇居民人均可支配收入的极差大于人均消费支出的极差 D、2017~2022年全国城镇居民人均消费支出占人均可支配收入的比例均大于80%

查看试题解析
19. 有一组样本数据 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{8}$ ，其中 $x_{1}$ 是最小值， $x_{8}$ 是最大值，则（）

A、 $x_{2} ， x_{3} ， x_{4} ， x_{5} ， x_{6} ， x_{7}$ 的平均数等于 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{8}$ 的平均数 B、 $x_{2} ， x_{3} ， x_{4} ， x_{5} ， x_{6} ， x_{7}$ 的中位数等于 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{8}$ 的中位数 C、 $x_{2} ， x_{3} ， x_{4} ， x_{5} ， x_{6} ， x_{7}$ 的标准差不小于 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{8}$ 的标准差 D、 $x_{2} ， x_{3} ， x_{4} ， x_{5} ， x_{6} ， x_{7}$ 的极差不大于 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{8}$ 的极差

查看试题解析
20. 甲、乙两个旅游景区某月初连续7天的日均气温数据如图所示（气温均取整数），则关于这7天的日均气温，下列判断正确的是（）

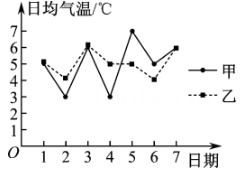A、甲旅游景区日均气温的平均数与乙旅游景区日均气温的平均数相等 B、甲旅游景区日均气温的中位数与乙旅游景区日均气温的中位数相等 C、甲旅游景区的日均气温波动比乙旅游景区的日均气温波动大 D、乙旅游景区日均气温的极差为 $1 ℃$

查看试题解析
21. 一组数据 $x_{i} (i = 1 ， 2 ， 3 ， ⋯ ， n)$ 的平均数为 $\bar{x}$ ，方差为 $s^{2}$ ，新数据 $a x_{i} + c (i = 1 ， 2 ， 3 ， ⋯ ， n)$ 的平均值为 ${\bar{x}}^{'}$ ，方差为 ${s^{'}}^{2}$ ．下列结论正确的是（）

A、 ${\bar{x}}^{'} = a \bar{x}$ B、 ${s^{'}}^{2} = a^{2} a^{2} + c$ C、 ${\bar{x}}^{'} = a \bar{x} + c$ D、 ${s^{'}}^{2} = a^{2} s^{2}$

查看试题解析
22. 某单位健康体测，男性平均体重为64千克，方差为151；女性平均体重为56千克，方差为159，男女人数之比为 $5 ： 3$ ，该单位全体工作人员平均体重 $\bar{x}$ 和方差 $s^{2}$ 分别为（）

A、 $\bar{x} = 61$ B、 $\bar{x} = 60$ C、 $s^{2} = 155$ D、 $s^{2} = 169$

查看试题解析
23. 已知一组样本数据 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{n} (n \geq 4)$ 均为正数，且 $x_{1} < x_{2} < \cdot \cdot \cdot < x_{n}$ ，若由 $y_{k} = 2 x_{k} - 1 (k = 1 ， 2 ， \cdot \cdot \cdot ， n)$ 生成一组新的数据 $y_{1} ， y_{2} ， \cdot \cdot \cdot ， y_{n}$ ，则这组新数据与原数据可能相等的是（）

A、平均数 B、极差 C、中位数 D、标准差

查看试题解析
24. 若甲组样本数据 $x_{1} ， x_{2} ， ⋯ ， x_{n}$ （数据各不相同）的平均数为3，乙组样本数据 $2 x_{1} + a ， 2 x_{2} + a ， ⋯ ， 2 x_{n} + a$ 的平均数为5，下列说错误的是（）

A、 $a$ 的值不确定 B、乙组样本数据的方差为甲组样本数据方差的2倍 C、两组样本数据的极差可能相等 D、两组样本数据的中位数可能相等

查看试题解析
25. 某校为了了解学生的身体素质，对2022届初三年级所有学生仰卧起坐一分钟的个数情况进行了数据统计，结果如图1所示.该校2023届初三学生人数较2022届初三学生人数上升了 $10 %$ ， $2023$ 届初三学生仰卧起坐一分钟的个数分布条形图如图2所示，则（）

A、该校2022届初三年级学生仰卧起坐一分钟的个数在 $[30 ， 60)$ 内的学生人数占 $70 %$ B、该校2023届初三学生仰卧起坐一分钟的个数在 $[60 ， 80]$ 内的学生人数比2022届初三学生仰卧起坐一分钟个数同个数段的学生人数的2.2倍还多 C、该校2023届初三学生仰卧起坐一分钟的个数和2022届初三学生仰卧起坐一分钟个数的中位数均在 $[50 ， 60)$ 内 D、相比2022届初三学生仰卧起坐一分钟个数不小于50的人数，2023届初三学生仰卧起坐一分钟个数不小于50的人数占比增加

查看试题解析
26. 为了进一步培养全校学生的法律意识，强化学生自我保护能力，知法守法，某中学举行法规知识竞赛（满分 $50$ 分），对全校参赛的 $1000$ 名学生的得分情况进行了统计，把得分数据按照 $[0 ， 10)$ 、 $[10 ， 20)$ 、 $[20 ， 30)$ 、 $[30 ， 40)$ 、 $[40 ， 50]$ 分成 $5$ 组，绘制了如图所示的频率分布直方图，根据图中信息，下列说法正确的是（）

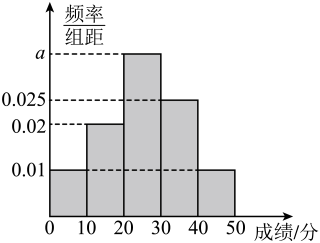A、 $a = 0.35$ B、得分在区间 $[10 ， 20)$ 内的学生人数为 $200$ C、该校学生法规竞赛成绩的中位数大于 $20$ D、估计该校学生法规竞赛成绩的平均数落在区间 $[30 ， 40)$ 内

查看试题解析
27. 已知一组样本数据 $x_{1}$ ， $x_{2}$ ， …， $x_{n} (n \geq 4)$ 均为正数，且 $x_{1} < x_{2} < ⋯ < x_{n}$ ，若由 $y_{k} = 2 x_{k} - 1 (k = 1 ， 2 ， ⋯ ， n)$ 生成一组新的数据 $y_{1}$ ， $y_{2}$ ， …， $y_{n}$ ，则这组新数据与原数据的（）可能相等.

A、极差 B、平均数 C、中位数 D、标准差

查看试题解析
28. 气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度（单位：℃）的记录数据（记录数据都是正整数）：
①甲地：5个数据的中位数为24，众数为22；
②乙地：5个数据的中位数为27，总体平均数为24；
③丙地：5个数据中有一个数据是32，总体平均数为26，总体方差为10.8.
则肯定进入夏季的地区有（）

A、一个都没有 B、甲地 C、乙地 D、丙地

查看试题解析

三、填空题

29. 某区为了解全区12000名高二学生的体能素质情况，在全区高二学生中随机抽取了1000名学生进行体能测试，并将这1000名的体能测试成绩整理成如下频率分布直方图．根据此频率分布直方图，这1000名学生平均成绩的估计值为．

查看试题解析
30. 数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的方差为 $\frac{1}{3} (x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) - 9$ ，则数据 $2 x_{1} + 1$ ， $2 x_{2} + 1$ ， $2 x_{3} + 1$ 的平均数为.

查看试题解析
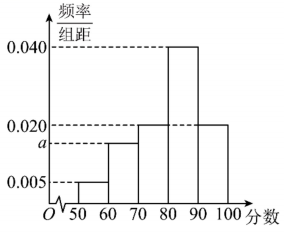31. 已知采用分层抽样得到的高三男生、女生各100名学生的身高情况为：男生样本平均数为172cm，方差为120，女生样本平均数165cm，方差为120，则总体样本方差是.

查看试题解析
32. 在对某工厂甲乙两车间某零件尺寸的调查中，采用分层抽样，如果不知道样本数据，只知道抽取了甲车间 $10$ 个零件，其尺寸的平均数和方差分别为 $12$ 和 $4.5$ ，抽取了乙车间 $30$ 个零件，其平均数和方差分别为 $16$ 和 $3.5$ ，则该工厂这种零件的方差估计值为 $($ 精确到 $0.1)$ ．

查看试题解析
33. 200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，则时速的众数、中位数的估计值分别为.

查看试题解析
34. 湖北省中药材研发中心整合省农业科技创新中心、省创新联盟相关资源和力量，为全省中药材产业链延链、补链、强链提供科技支撑，某科研机构研究发现，某品种中医药的药物成分甲的含量x（单位：g与药物功效y（单位：药物单位）之间满足 $y = 15 x - 2 x^{2}$ ，检测这种药品一个批次的6个样本，得到成分甲的含量x的平均值为5g，标准差为 $\sqrt{5}$ g，则估计这批中医药的药物功效y的平均值为药物单位．

查看试题解析

四、解答题

35. 某稻谷试验田试种了 $A$ ， $B$ 两个品种的水稻各10亩，并在稻谷成熟后统计了这20亩地的稻谷产量如下表，记 $A$ ， $B$ 两个品种各10亩产量的平均数分别为 $\bar{x}$ 和 $\bar{y}$ ，方差分别为 $S_{1}^{2}$ 和 $S_{2}^{2}$ ．
$A$ （单位： $10 k g$ ）
60
63
50
76
71
85
75
63
63
64
$B$ （单位： $10 k g$ ）
56
62
60
68
78
75
76
62
63
70

(1)、分别求这两个品种产量的极差和中位数；

(2)、求 $\bar{x}$ ， $\bar{y}$ ， $S_{1}^{2}$ ， $S_{2}^{2}$ ；

(3)、依据以上计算结果进行分析，推广种植 $A$ 品种还是 $B$ 品种水稻更合适．

查看试题解析
36. 为了迎接新高考，某校举行物理和化学等选科考试，其中，600名学生化学成绩（满分100分）的频率分布直方图如图所示，其中成绩分组区间是：第一组 $[45 ， 55)$ ，第二组 $[55 ， 65)$ ，第三组 $[65 ， 75)$ ，第四组 $[75 ， 85)$ ，第五组 $[85 ， 95)$ .已知图中第三组频率为 $0.45$ ，第一组和第五组的频率相同.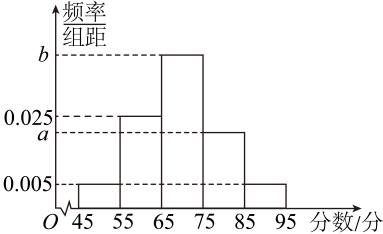

(1)、求a ， b的值；

(2)、估算高分（大于等于80分）人数；

(3)、估计这600名学生化学成绩的平均值（同一组中的数据用该组区间的中点值作代表）和中位数.（中位数精确到0.1）

查看试题解析
37. 随着老年人消费需求从“生存型”向“发展型”转变．消费层次不断提升，“银发经济”成为社会热门话题之一，被各企业持续关注.某企业为了解该地老年人消费能力情况，对该地年龄在 $[60 ， 80)$ 的老年人的年收入按年龄 $[60 ， 70)$ ， $[70 ， 80)$ 分成两组进行分层抽样调查，已知抽取了年龄在 $[60 ， 70)$ 的老年人500人．年龄在 $[70 ， 80)$ 的老年人300人．现作出年龄在 $[60 ， 70)$ 的老年人年收入的频率分布直方图（如下图所示）．

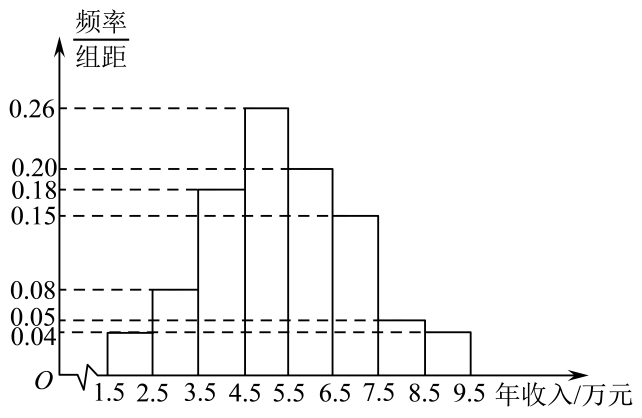(1)、根据频率分布直方图，估计该地年龄在 $[60 ， 70)$ 的老年人年收入的平均数及第95百分位数；

(2)、已知年龄在 $[60 ， 70)$ 的老年人年收入的方差为3，年龄在 $[70 ， 80)$ 的老年人年收入的平均数和方差分别为3.75和1.4，试估计年龄在 $[60 ， 80)$ 的老年人年收入的方差．

查看试题解析

$A$ （单位： $10 k g$ ）	60	63	50	76	71	85	75	63	63	64
$B$ （单位： $10 k g$ ）	56	62	60	68	78	75	76	62	63	70

组号	1	2	3	4	5
频数	8	11	10	$x$	9

2023-2024学年高中数学人教A版必修二 9.2 用样本估计总体 同步练习

一、选择题

二、多项选择题

三、填空题

四、解答题

2023-2024学年高中数学人教A版必修二 9.2 用样本估计总体同步练习