【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略13 一元一次不等式（组）

试卷更新日期：2023-12-15 类型：复习试卷

进入出卷网下载

一、选择题

1. 以下是一元一次不等式的是（）

A、x+y＞0 B、 $\frac{x}{2}$ >0 C、x²≠3 D、3＞1

查看试题解析
2. 如图所示，在数轴上表示不等式正确的是（）

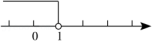A、x＜1 B、x≤1 C、x＞1 D、x≥1

查看试题解析
3. 不等式 $x - 1 < 0$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，该数轴表示的不等式的解集为（）

A、 $x < 2$ B、 $x > 1$ C、 $0 < x < 2$ D、 $1 < x < 2$

查看试题解析
5. 在平面直角坐标系中，若点 $P (2 - m ， 7 - 2 m)$ 在第二象限，则整数m的值为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 若关于x的不等式组 ${\begin{cases} x < 2 (x - a) \\ x - 1 \leq \frac{2}{3} x \end{cases}$ 恰有3个整数解，则a的取值范围是（）

A、 $0 \leq a < \frac{1}{2}$ B、 $0 \leq a < 1$ C、 $- \frac{1}{2} < a \leq 0$ D、 $- 1 \leq a < 0$

查看试题解析
7. 小聪用100元钱去购买笔记本和钢笔共30件.已知每本笔记本2元，每支钢笔5元，小聪最多可以购买钢笔多少支？设小聪最多能买x支钢笔.可列出不等式（）

A、 $5 x + 2 (30 - x) < 100$ B、 $5 x + 2 (30 - x) \leq 100$ C、 $5 x + 2 (30 - x) \geq 100$ D、 $5 x + 2 （ 30 - x ） > 100$

查看试题解析
8. 为了美化校园，学校决定利用现有的2660盆甲种花卉和 $3000$ 盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内，已知搭配一个A种造型需甲种花卉70盆，乙种花卉 $30$ 盆，搭配一个B种造型需甲种花卉40盆，乙种花卉 $80$ 盆.设搭配A种造型x个，你认为下列符合题意的不等式组是（）

A、 ${\begin{array}{l} 70 x + 40 (50 - x) \leq 2660 \\ 30 x + 80 (50 - x) \leq 3000 \end{array}$ B、 ${\begin{array}{l} 70 x + 40 (50 - x) < 2660 \\ 30 x + 80 (50 - x) < 3000 \end{array}$ C、 ${\begin{array}{l} 70 x + 40 (50 - x) \geq 2660 \\ 30 x + 80 (50 - x) \geq 3000 \end{array}$ D、 ${\begin{array}{l} 70 x + 40 (50 - x) > 2660 \\ 30 x + 80 (50 - x) > 3000 \end{array}$

查看试题解析
9. 对于任意实数p、q，定义一种运算： $p @ q = p + q - pq$ ，如： $2 @ 3 = 2 + 3 - 2 \times 3$ ，请根据以上定义解决问题：若关于x的不等式组 ${\begin{matrix} 2 @ x > 0 \\ x @ 3 \leq m \end{matrix}$ 有2个整数解，则m的取值范围为是（）

A、3≤m<5 B、3<m≤5 C、3≤m≤5 D、3<m<5

查看试题解析
10. 下列按条件列不等式正确的是（）

A、若 $a$ 是非负数，则 $a \geq 0$ B、若 $x$ 的值不大于3，则 $x < 3$ C、若 $m$ 与 $- 1$ 的和小于或等于0，则 $m + 1 \leq 0$ D、若 $x$ 的值不小于1，则 $x > 1$

查看试题解析

二、填空题

11. 若x是非正数，则x0.（填不等号）

查看试题解析
12. 不等式（a﹣b）x＜a﹣b的解集是x＞1，则a、b的大小关系是：ab．

查看试题解析
13. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} x - 4 a < 0 \\ 3 x - 2 < 7 x - 6 \end{array}$ 无解，则 $a$ 的取值范围是

查看试题解析

14. 嘉兴某玩具城计划购进

A

、

B

、

C

三种玩具，其进价和售价.如下表：

玩具名称	进价（元/件）	售价（元/件）
$A$	40	50
$B$	70	100
$C$	80	120

现在用6800元购买100件玩具，若销售完这些玩具获得的最大利润是3000元，则 $A$ 玩具最多购进件.

查看试题解析

15. 定义：对于实数a，符号 $[a]$ 表示不大于a的最大整数.例如： $[5.7] = 5$ ， $[5] = 5$ ， $[- π] = - 4$ .如果 $[\frac{x + 1}{2}] = 3$ ，则满足条件的所有正整数x的值是.

查看试题解析
16. 运行程序如图所示，规定：从“输入一个值 $x$ ”到“结果是否 $> 94$ ”为一次程序操作，如果程序操作进行了三次才停止，那么 $x$ 的取值范围是.

查看试题解析

三、解答题

17. 解不等式（组）：

(1)、5x-2＞x+1；

(2)、 ${\begin{cases} 4 (x + 1) < 7 x + 13 \\ 2 x - 4 < \frac{x - 8}{3} \end{cases}$ ．

查看试题解析
18. 求适合不等式 $\frac{1 - x}{4}$ >-2x的最小整数解．

查看试题解析
19. 沙棘是一种耐旱、固沙的植物，被广泛用于水土保持．某市地处沙漠边沿，为了防止土地荒漠化，该市原计划2011年到2021年每年种植30公顷沙棘.2018年之前都按原计划种植，从2018年开始，年种植量比原计划增加了，且2018年到2021年这4年的沙棘种植总面积不少于前几年的种植总面积．从2018年开始，该市的沙棘年种植面积至少比原计划增加多少公顷？

查看试题解析
20. 某市电力部门]实行两种电费计价方法．方法一是使用“峰谷电”：每天8：00至22：00，用电每千瓦时收费0.56元（“峰电”价）；22 ：00到次日8：00，每千瓦时收费0.28元（“谷电”价）．方法二是不使用“峰谷电”：每千瓦时均收费0.53元如果小林家上月总用电量为140千瓦时，那么当“峰电”用量为多少时，使用“峰谷电”比较合算？

查看试题解析
21. 已知关于 x，y 的二元一次方程组 ${\begin{array}{l} 3 x - 4 y = k \\ 2 x - 3 y = 2 k + 3 \end{array}$ 的解满足 $x - y < 0$ .

(1)、求 k 的取值范围；

(2)、在 (1) 的条件下，若不等式 $(2 k + 1) x - 2 k < 1$ 的解为 $x > 1$ ，请写出符合条件的 k 的整数值.

查看试题解析
22. 已知关于x、y的二元一次方程组 ${\begin{array}{l} 2 x - y = 3 k - 2 \\ 2 x + y = 1 - k \end{array}$ （k为常数）．

(1)、求这个二元一次方程组的解（用含k的代数式表示）；

(2)、若方程组的解x、y满足x+y＞5，求k的取值范围；

(3)、若k≤1，设m＝2x﹣3y，且m为正整数，求m的值．

查看试题解析
23. 深化理解：
新定义：对非负实数x“四舍五入”到个位的值记为＜x＞，
即：当n为非负整数时，如果n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ ，则＜x＞=n；
反之，当n为非负整数时，如果＜x＞=n，则n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ ．
例如：＜0＞=＜0.48＞=0，＜0.64＞=＜1.49＞=1，＜2＞=2，＜3.5＞=＜4.12＞=4，…
试解决下列问题：

(1)、填空：①＜π＞=（π为圆周率）； ②如果＜x﹣1＞=3，则实数x的取值范围为．

(2)、若关于x的不等式组 ${\begin{matrix} \frac{2 x - 4}{3} \leq x - 1 \\ < a > - x > 0 \end{matrix}$ 的整数解恰有3个，求a的取值范围．

(3)、求满足＜x＞= $\frac{4}{3}$ x 的所有非负实数x的值．

查看试题解析