【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略11 勾股定理及其逆定理
试卷更新日期:2023-12-15 类型:复习试卷
一、选择题
-
1. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、1,2, C、1, , D、4,5,62. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、 ,3. 有一直角三角形纸片,∠C=90°BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
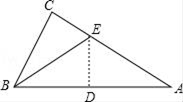 A、 B、 C、 D、44. 若Rt的两边长为5和12,则第三边长为( )A、13 B、26 C、 D、13或5. 《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”
A、 B、 C、 D、44. 若Rt的两边长为5和12,则第三边长为( )A、13 B、26 C、 D、13或5. 《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B’(如图).则这根芦苇的长度是( )
 A、10尺 B、11尺 C、12尺 D、13尺6. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( )
A、10尺 B、11尺 C、12尺 D、13尺6. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( ) A、16 B、17 C、18 D、197. 勾股定理是我国的伟大数学发明之一.如图,以的各边为边向外作正方形,再把较小的两张正方形纸片放入最大的正方形中,三个阴影部分的面积分别为 , , , 则较小两个正方形重叠部分(四边形)的面积为( )
A、16 B、17 C、18 D、197. 勾股定理是我国的伟大数学发明之一.如图,以的各边为边向外作正方形,再把较小的两张正方形纸片放入最大的正方形中,三个阴影部分的面积分别为 , , , 则较小两个正方形重叠部分(四边形)的面积为( )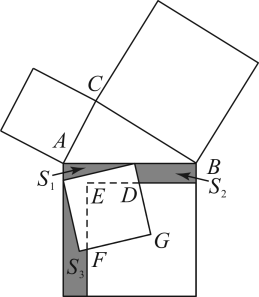 A、4 B、5 C、5.5 D、68. 如图,A,B,C,D四个点顺次在直线l上,.以为底向下作等腰直角三角形 , 以为底向上作等腰三角形 , 且.连接 , 当的长度变化时,与的面积之差保持不变,则a与b需满足( )
A、4 B、5 C、5.5 D、68. 如图,A,B,C,D四个点顺次在直线l上,.以为底向下作等腰直角三角形 , 以为底向上作等腰三角形 , 且.连接 , 当的长度变化时,与的面积之差保持不变,则a与b需满足( ) A、 B、 C、 D、9. 如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S4=( )
A、 B、 C、 D、9. 如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+S4=( ) A、2 B、3 C、4 D、610. 己如等边 的边长为4,点P是边 上的动点,将 绕点A逆时针旋转 得到 ,点D是 边的中点,连接 ,则 的最小值是( )
A、2 B、3 C、4 D、610. 己如等边 的边长为4,点P是边 上的动点,将 绕点A逆时针旋转 得到 ,点D是 边的中点,连接 ,则 的最小值是( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
11. 直角三角形两条边长分别为3和4,则第三边的长为.12. 直角三角形的两条直角边长为5和12,则斜边上的中线长是 .13. 如图,有两棵树,一棵高10m,另一棵高4m,两树相距8m.一只小鸟从一棵树的树尖飞到另一棵树的树尖,那么这只小鸟至少要飞行m.
 14. 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度相等,滑梯的高度 , .则滑道的长度为m.
14. 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度相等,滑梯的高度 , .则滑道的长度为m.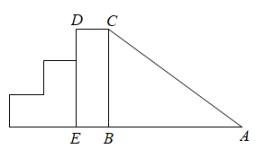 15. 如图四边形中, , 则四边形面积为.
15. 如图四边形中, , 则四边形面积为. 16. 如图,在以点为直角顶点的中, , , 点是边的中点,以为底边向上作等腰 , 使得 , 交于点 , 则.
16. 如图,在以点为直角顶点的中, , , 点是边的中点,以为底边向上作等腰 , 使得 , 交于点 , 则.
三、解答题
-
17. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.18. 如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,连结AE,求BE的长.
 19. 如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE=BF.
19. 如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.求证:CE=BF. 20. 如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B′离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
20. 如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B′离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.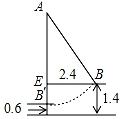 21. 我们新定义一种三角形:两边平方和等于第三边平方的3倍的三角形叫做常态三角形.例如:某三角形三边长分别是3,6和 , 因为32+62=3×2=45,所以这个三角形是常态三角形.
21. 我们新定义一种三角形:两边平方和等于第三边平方的3倍的三角形叫做常态三角形.例如:某三角形三边长分别是3,6和 , 因为32+62=3×2=45,所以这个三角形是常态三角形. (1)、若△ABC三边长分别是2,3和 , 则此三角形常态三角形(填“是”或“不是”);(2)、若Rt△ABC是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD , 若△BCD是常态三角形,求AC的长。
(1)、若△ABC三边长分别是2,3和 , 则此三角形常态三角形(填“是”或“不是”);(2)、若Rt△ABC是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD , 若△BCD是常态三角形,求AC的长。

