沪科版数学八年级上册第15章轴对称图形和等腰三角形同步课堂测试

试卷更新日期：2023-12-15 类型：同步测试

进入出卷网下载

一、选择题

1. 下列图形中，不是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列说法中，正确的有（）个
①两个全等的三角形一定关于某直线对称；
②关于某条直线对称的两个图形，对称点所连线段被对称轴垂直平分；
③等腰三角形的高、中线、角平分线互相组合；
④到三角形三个顶点距离相等的点是这个三角形三边垂直平分线的交点；
⑤ $△ A B C$ 的三边为a，b，c，且满足关系 $(a - b) (b - c) (c - a) = 0$ ，则 $△ A B C$ 为等边三角形.

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图， $∠ A O B = 30 °$ ，点 $P$ 是 $∠ A O B$ 内的定点且 $O P = 3$ ，若点M、N分别是射线OA、OB上异于点 $O$ 的动点，则 $△ P M N$ 周长的最小值是（）

A、3 B、 $\frac{2}{3}$ C、 $\frac{4}{3}$ D、6

查看试题解析
4. 如下图，地面上有三个洞口A、B、C，老鼠可从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口，尽快抓住老鼠，应该蹲在（）

A、 $△ A B C$ 三条角平分线的交点 B、 $△ A B C$ 三条边的中线的交点 C、 $△ A B C$ 三条高的交点 D、 $△ A B C$ 三条边的垂直平分线的交点

查看试题解析
5. 如图，等腰直角△ABC中，AC＝BC，∠ACB＝90°，D为AC边上一动点（不与A、C重合），过点A作AE垂直BD于点E，延长AE交BC的延长线于点F，连接CE，则 $∠ B E C$ 为（）

A、30° B、36° C、45° D、60°

查看试题解析
6. 如图，△ABC是等腰直角三角形，AB＝AC ，已知点A的坐标为（-2，0），点B的坐标为（0，1），则点C的坐标为（　　）

A、（-3，1.5） B、（-4，1.5） C、（-3，2） D、（-4，2）

查看试题解析
7. 如图，点E ， F分别为长方形纸片ABCD的边AB ， CD上的点，将长方形纸片沿EF翻折，点C ， B分别落在点C'，B'处．若∠DFC'＝α，则∠FEA-∠AEB'的度数为（　　）

A、 $4 5^{°} + \frac{1}{2} α$ B、 $6 0^{°} - \frac{1}{2} α$ C、 $9 0^{°} - \frac{1}{2} α$ D、 $6 0^{°} - \frac{3}{2} α$

查看试题解析
8. 如图，图1是AD∥BC的一张纸条，按图1→图2→图3的顺序，把这一纸条先沿EF折叠并压平，再沿BF折叠并压平，若图3中∠CFE=18°，则∠AEF的度数为 (　　)

A、120°　　　　 B、108°　　　　 C、126°　　　　 D、114°

查看试题解析

二、填空题

9. 如图，在△ABC中，∠ACB=∠ABC=40^o ， BD是∠ABC的角平分线，延长BD至点E，使得DE=DA，则∠ECA=.

查看试题解析
10. 如图， $△ A B C$ 为等腰直角三角形 $A C = B C$ ，若 $A (- 3 ， 0)$ ， $C (0 ， 2)$ ，则点B的坐标为.

查看试题解析
11. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D F ⊥ A B$ ，垂足为F， $D E = D G$ ， $△ A D G$ 和 $△ A E D$ 的面积分别为27和14，则 $△ E D F$ 的面积为．

查看试题解析
12. 如图，△ABC中，AB=4，BC=5，CA=6，三条角平分线交于点O．△CAO的面积等于9，则△ABO的面积= ．

查看试题解析
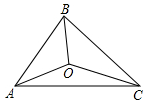13. 如图（1）的长方形ABCD中，E点在AD上，且BE＝2AE ．今分别以BE、CE为折线，将A、D向BC的方向折过去，图（2）为对折后A、B、C、D、E五点均在同一平面上的位置图．若图（2）中，∠AED＝15°，则∠BCE的度数为．

查看试题解析

三、解答题

14. 在等腰 $△ A B C$ 中， $A B = 8$ ， $B C = 2 m + 2$ ， $A C = 20$ ，求m的值．

查看试题解析

四、综合题

15. 已知 $△ A B C$ 的三边长分别为 $m + 2$ ， $2 m$ ， 8．

(1)、求 $m$ 的取值范围；

(2)、如果 $△ A B C$ 是等腰三角形，求 $m$ 的值．

查看试题解析
16. 已知，如图， $△ A B C$ 为等边三角形， $A E = C D ， A D 、 B E$ 相交于点 $P$ .

(1)、求证： $△ A E B ≌ △ C D A$ ；

(2)、求 $∠ E P Q$ 的度数；

(3)、若 $B Q ⊥ A D$ 于 $Q ， P Q = 7 ， P E = 3$ ，求 $B E$ 的长.

查看试题解析
17. 如果一个三角形被一条线段分割成两个等腰三角形，那么这种分割叫做等腰分割，这条线段称为这个三角形的等腰分割线．如图1，当△ABD和△ACD为等腰三角形时，AD为△ABC的等腰分割线．

(1)、如图2，△ABC中，∠B＝2∠C，线段AC的垂直平分线ED交AC于点D，交BC于点E．求证：AE是△ABC的一条等腰分割线．

(2)、如图3，在△ABC中，∠A＝120°，∠B＝20°，∠C＝40°，请你用两种不同的方法完成△ABC的等腰分割，并在图中标注底角的度数．

(3)、在△ABC中，AD为△ABC的等腰分割线，且AD＝BD，∠C＝30°，请直接写出∠A的度数．

查看试题解析
18. 如图，在等边 $△ A B C$ 中，点D，E分别在边 $A C ， A B$ 上，且 $A D = B E$ ， $B D ， C E$ 交于点P， $C F ⊥ B D$ ，垂足为点F．

(1)、求证： $B D = C E$ ；

(2)、若 $C P = 7$ ，求 $P F$ 的长．

查看试题解析
19. 如图， $Δ A B C$ 是等边三角形，延长 $B C$ 到 $E ，$ 使 $C E = \frac{1}{2} B C$ ．点 $D$ 是边 $A C$ 的中点，连接 $E D$ 并延长交 $A B$ 于 $F$ ．

(1)、求 $∠ E F B$ 的度数；

(2)、求证： $D E = 2 D F$ ．

查看试题解析
20. 如图，点 $O$ 是等边 $△ A B C$ 内一点， $D$ 是 $△ A B C$ 外的一点， $∠ A O B = 110 °$ ， $∠ B O C = α$ ， $△ B O C ≌ △ A D C$ ， $∠ O C D = 60 °$ ，连接 $O D$ ．

(1)、求证： $Δ O C D$ 是等边三角形；

(2)、当 $α = 150 °$ 时，试判断 $△ A O D$ 的形状，并说明理由：

(3)、探究：当 $α$ 为多少度时， $O D = A D$ ？

查看试题解析
21. 在等腰三角形△ABC中， $A C = B C$ ， D、E分别为AB、BC上一点， $∠ C D E = ∠ A$ ．

(1)、如图1，若 $B C = B D$ ，求证： $△ A D C ≅ △ B E D$ ；

(2)、如图2，过点C作 $C H ⊥ D E$ ，垂足为H，若 $C D = B D$ ， $E H = 3$ ．
①求证： $C E = D E$ ；
②求CE－BE的值．

查看试题解析
22. 如图， $C N$ 是等边 $△ A B C$ 的外角 $∠ A C M$ 内部的一条射线，点 $A$ 关于 $C N$ 的对称点为 $D$ ，连接 $A D$ ， $B D$ ， $C D$ ，其中 $A D$ ， $B D$ 分别交射线 $C N$ 于点 $E$ ， $P$ ．

(1)、求证： $△ B C D$ 是等腰三角形；

(2)、若 $∠ A C N = α$ ，求 $∠ B D C$ 的大小（用含 $α$ 的式子表示）；

(3)、求证： $P B = P C + 2 P E$ ．

查看试题解析

沪科版数学八年级上册第15章 轴对称图形和等腰三角形 同步课堂测试

一、选择题

二、填空题

三、解答题

四、综合题

沪科版数学八年级上册第15章轴对称图形和等腰三角形同步课堂测试