2023-2024学年初中数学沪科版七年级上册 4.5 角的比较与补(余)角 同步分层训练培优卷
试卷更新日期:2023-12-15 类型:同步测试
一、选择题
-
1. 如果一个角是 , 那么它的补角等于( )A、 B、 C、 D、2. 钟面上点分,时针和分针所成的角是( )A、 B、 C、 D、3. 下列说法:①两点确定一条直线;②两点之间,线段最短;③若 , 则射线是的平分线;④连接两点之间的线段叫做这两点间的距离;⑤学校在小明家南偏东方向上,则小明家在学校北偏西方向上.其中正确的有( )A、1个 B、2个 C、3个 D、4个4. 如图,点在直线上,、分别平分、 , 则图中互为余角的有( )对
 A、1 B、2 C、3 D、45. 已知是锐角,与互补,与互余,则的度数为( )A、 B、 C、 D、6. 如图,∠AOB的大小为( )
A、1 B、2 C、3 D、45. 已知是锐角,与互补,与互余,则的度数为( )A、 B、 C、 D、6. 如图,∠AOB的大小为( )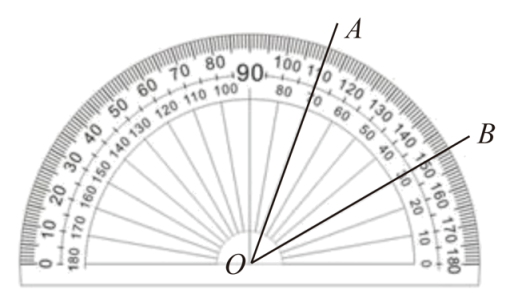 A、 B、 C、 D、7. 如图,C,D在线段上,下列四个说法:
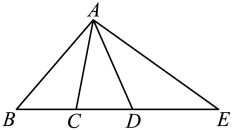
A、 B、 C、 D、7. 如图,C,D在线段上,下列四个说法:①直线上以B,C,D,E为端点的线段共有6条;
②图中有3对互为补角的角;
③若 , , 则以A为顶点的所有小于平角的角的度数和为370°;
④若 , , , 点F是线段上任意一点(包含端点),则点F到点B,C,D,E的距离之和的最小值为15,最大值为25
其中正确说法的个数是( )
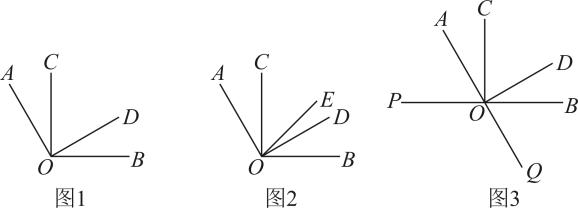
 A、1个 B、2个 C、3个 D、4个8. 如图,已知射线 , , 依次作出的角平分线 , 的角平分线 , 的角平分线的角平分线 , 其中点都在射线上,则的度数为( )
A、1个 B、2个 C、3个 D、4个8. 如图,已知射线 , , 依次作出的角平分线 , 的角平分线 , 的角平分线的角平分线 , 其中点都在射线上,则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,将含有的直角三角板的两个顶点分别放在直尺的一组对边上,如果 , 那么°.
 10. 定义:从一个角的顶点引一条射线,把这个角分成两个角,并且这两个角的度数之比为1:2,这条射线叫做这个角的三分线.显然,一个角的三分线有两条.如 , , 是的两条三分线,以点为中心,将按顺时针方向旋转()得到 , 当恰好是的三分线时,的值为 .
10. 定义:从一个角的顶点引一条射线,把这个角分成两个角,并且这两个角的度数之比为1:2,这条射线叫做这个角的三分线.显然,一个角的三分线有两条.如 , , 是的两条三分线,以点为中心,将按顺时针方向旋转()得到 , 当恰好是的三分线时,的值为 . 11. 直线、相交于点 , 平分 , 平分 , 且 , 则的度数是 .
11. 直线、相交于点 , 平分 , 平分 , 且 , 则的度数是 . 12. 已知 , 如图1,过作射线、 , 如图2,过作射线、 , 使 , , , , 则 .
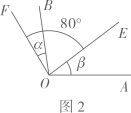
12. 已知 , 如图1,过作射线、 , 如图2,过作射线、 , 使 , , , , 则 .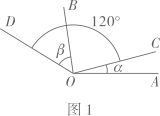
 13. 如图,∠AOB=40°,自点O引射线OC,若∠AOC:∠COB=2∶3,则OC与∠AOB的平分线所成的角的度数为
13. 如图,∠AOB=40°,自点O引射线OC,若∠AOC:∠COB=2∶3,则OC与∠AOB的平分线所成的角的度数为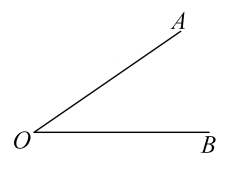
三、解答题
-
14. 如图,直线、相交于点O, , 若 , , 求度数.
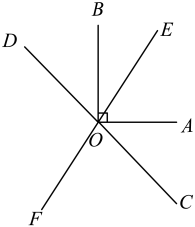 15. 如图,直线和相交于点O, , 垂足为O,平分 , 若 , 求的度数.
15. 如图,直线和相交于点O, , 垂足为O,平分 , 若 , 求的度数.
四、综合题