2023-2024学年初中数学沪科版七年级上册 4.3 线段的长短比较同步分层训练培优卷

试卷更新日期：2023-12-15 类型：同步测试

进入出卷网下载

一、选择题

1. 已知线段AB＝8，BC＝3，且A，B，C三点在同一条直线上，则AC的长是（）

A、5 B、11 C、5或11 D、24

查看试题解析
2. 如图，D是AB的中点，E是BC的中点，若AD=6，BC=8，则下列说法中错误的是（）

A、AC=20 B、DC=16 C、DE=10 D、BE=4

查看试题解析
3. 已知线段 $A B = 10$ cm，点C是线段AB上任意一点，则线段AC中点与线段BC中点之间的距离是（）

A、3cm B、4cm C、5cm D、无法计算

查看试题解析
4. 在下列生活、生产现象中，可以用基本事实“两点之间，线段最短”来解释的是（）
①用两颗钉子就可以把木条固定在墙上；②在A、B两地之间架设电线时，总是尽可能沿线段AB架设；③植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上；④把弯曲的公路改直，就能缩短路程.

A、①② B、①③ C、②④ D、③④

查看试题解析
5. 如图，在三角形ABC中，线段AB+AC>BC，其理由是（）

A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、同一平面内，过一点有且只有一条直线垂直于已知直线

查看试题解析
6. 在数轴上，点M、N分别表示数m，n.则点M、N之间的距离为 $| m - n |$ .已知点A，B，C，D在数轴上分别表示的数为a，b，c，d.且 $| a - c | = | b - c | = 2 ， \frac{2}{5} | d - a | = 1 (a \neq b)$ ，则线段 $B D$ 的长度为（）

A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.5

查看试题解析
7. 如图所示：把两个正方形放置在周长为 $m$ 的长方形 $A B C D$ 内，两个正方形的重叠部分的周长为 $n$ (图中阴影部分所示)，则这两个正方形的周长和可用代数式表示为（）

A、 $m + n$ B、 $m - n$ C、 $2 m - n$ D、 $m + 2 n$

查看试题解析
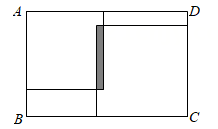8. 已知，点C在直线 AB 上， AC=a ， BC=b ，且 a≠b ，点 M是线段 AB 的中点，则线段 MC的长为（）

A、 $\frac{a + b}{2}$ B、 $\frac{a - b}{2}$ C、 $\frac{a + b}{2}$ 或 $\frac{a - b}{2}$ D、 $\frac{a + b}{2}$ 或 $\frac{| a - b |}{2}$

查看试题解析

二、填空题

9. 如图，已知线段 $A B = 12 c m$ ，点 $C$ 是线段 $A B$ 上的任意一点，点 $D ， E$ 分别是线段 $A C$ 和 $B C$ 的中点，则线段 $D E =$ $c m$ .

查看试题解析
10. 在数轴上，到原点的距离等于3的点所表示的数是.

查看试题解析
11. 金秋十月，不仅是丰收的季节，而且到处是色彩斑斓的景色，太原市迎泽公园藏着银杏叶极致的风景．小明同学捡到一片沿直线被折断了的银杏叶（如图），他发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是．

查看试题解析
12. 如图，C，D是线段AB上两点，且点C在点D的左侧，M，N分别是线段 $A D$ ， $B C$ 的中点．若 $A D = B M$ ， $B D = 3$ ，则AB的长为．

查看试题解析
13. 有一无弹性细线，拉直时测得细线 $O P$ 长为 $8 cm$ ，现进行如下操作：1.在细线上任取一点 $A$ ；2.将细线折叠，使点 $O$ 与点 $A$ 重合，记折点为点 $B$ ；3.将细线折叠，使点 $P$ 与点 $A$ 重合，记折点为点 $C$ .

(1)、如图， $B C$ 的长为 $cm$ ；

(2)、继续进行折叠，使点 $B$ 与点 $C$ 重合，并把 $B$ 点和与其重叠的 $C$ 点处的细线剪开，使细线分成长为 $a$ ， $b$ ， $c$ 的三段 $(a < b < c)$ ，当 $a ： b = 1 ： 3$ ，则细线未剪开时 $O A$ 的长为 $cm$ .

查看试题解析

三、解答题

14. 如图，D是线段 $A C$ 的中点，E是线段 $A B$ 的中点.已知 $A D = 6 c m$ ， $B C = 3 c m$ .求线段 $A B$ 和 $E C$ 的长度.

查看试题解析
15. 如图，点P为线段 $A B$ 上一点，延长 $A B$ 至Q，使得 $A P = 2 B Q$ ，点M为 $P B$ 的中点，点N为 $M Q$ 的中点，求 $\frac{N Q}{A B}$ 的值.

查看试题解析

四、综合题

16. 如图，已知数轴上 $A$ ， $B$ 两点对应的数分别为 $- 26$ ， $- 10$ ， $B$ ， $C$ 两点对应的数互为相反数.

(1)、求 $A B$ ， $A C$ 的长.

(2)、若点 $M$ 从 $A$ 点出发，以每秒1个单位长度的速度向终点 $C$ 运动.当点 $M$ 到达 $B$ 点时，点 $N$ 从 $A$ 点出发，以每秒3个单位长度的速度向终点 $C$ 运动，设 $M$ 点的移动时间为 $t$ （秒）.
①问 $t$ 为何值时， $B$ 为 $M N$ 的中点？

②当 $M N = \frac{1}{6} A C$ 时，求 $t$ 的值.

查看试题解析
17. 如图，点 $C$ 是直线 $A B$ 上一点，点 $M$ 是线段 $A C$ 的中点.

(1)、若 $A B = 8$ ，点 $C$ 在线段 $A B$ 上，且 $A C = 3 B C$ ，则 $A M$ 的长为.

(2)、若 $A B = a$ ， $A B - A C = \frac{a}{3}$ ，求 $B M$ 的长（用含 $a$ 的代数式表示）.

查看试题解析

2023-2024学年初中数学沪科版七年级上册 4.3 线段的长短比较 同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学沪科版七年级上册 4.3 线段的长短比较同步分层训练培优卷