2023-2024学年初中数学沪科版七年级上册 4.1 几何图形 同步分层训练培优卷
试卷更新日期:2023-12-15 类型:同步测试
一、选择题
-
1. 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成(第6题图)体,则下列序号中不应剪去的是( )
 A、6 B、3 C、2 D、12. 如图是一个正方体的平面展开图,若将展开图折叠成正方体后,相对面上所标的两个数相等,则a-b+c的值为( )
A、6 B、3 C、2 D、12. 如图是一个正方体的平面展开图,若将展开图折叠成正方体后,相对面上所标的两个数相等,则a-b+c的值为( )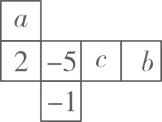 A、6 B、4 C、2 D、-43. 下面几何体中,不能由一个平面图形通过旋转得到的是A、
A、6 B、4 C、2 D、-43. 下面几何体中,不能由一个平面图形通过旋转得到的是A、 B、
B、 C、
C、 D、
D、 4. 如图,在一个正方形盒子的六面上写有“祝、母、校、更、美、丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对面上,则这个盒子的展开图(不考虑文字方向)不可能的是( )
4. 如图,在一个正方形盒子的六面上写有“祝、母、校、更、美、丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对面上,则这个盒子的展开图(不考虑文字方向)不可能的是( )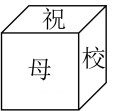 A、
A、 B、
B、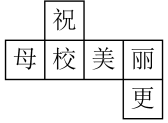 C、
C、 D、
D、 5. 你见过一种折叠灯笼吗?它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( )
5. 你见过一种折叠灯笼吗?它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( ) A、点动成线 B、线动成面 C、面动成体 D、面与面相交的地方是线6. 如图,是正方体包装盒的表面积展开图,如在其中的三个正方形、、、内分别填上适当的数,使得将这个表面积展开图沿虚线折成正方形后,相对面上的两数字互为相反数,则填在、、内的三个数字依次为( )
A、点动成线 B、线动成面 C、面动成体 D、面与面相交的地方是线6. 如图,是正方体包装盒的表面积展开图,如在其中的三个正方形、、、内分别填上适当的数,使得将这个表面积展开图沿虚线折成正方形后,相对面上的两数字互为相反数,则填在、、内的三个数字依次为( ) A、0,1,-2 B、0,-2,1 C、1,0,-2 D、-2,0,17. 在正方体的表面上画有如图1中所示的粗线,图2是其展开图的示意图,但只在A面上画有粗线,那么将图1中剩余两个面中的粗线画入图2中,画法正确的是( )
A、0,1,-2 B、0,-2,1 C、1,0,-2 D、-2,0,17. 在正方体的表面上画有如图1中所示的粗线,图2是其展开图的示意图,但只在A面上画有粗线,那么将图1中剩余两个面中的粗线画入图2中,画法正确的是( )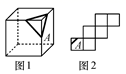 A、
A、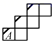 B、
B、 C、
C、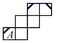 D、
D、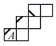 8. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .
8. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .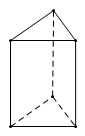 A、28 B、31 C、34 D、36
A、28 B、31 C、34 D、36二、填空题
-
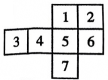
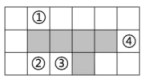
9. 如图,在有序号的小正方形中选出一个,它与图中五个有阴影的小正方形组合后,能构成正方体的表面展开图的是 .
 10. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,a-b= .
10. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,a-b= .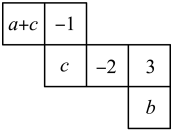 11. 子弹从枪膛中射出去的轨迹可看成一条线,这说明 的数学道理.12. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.13. 十八世纪数学家欧拉证明了简单多面体中顶点数( ),面数( ),棱数( )之间存在一个有趣的数量关系: ,这就是著名的欧拉定理.某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形拼接而成,且有24个顶点,每个顶点都有3条棱,设该多面体外表面三角形个数是 个,八边形的个数是 ,则x+y= .
11. 子弹从枪膛中射出去的轨迹可看成一条线,这说明 的数学道理.12. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.13. 十八世纪数学家欧拉证明了简单多面体中顶点数( ),面数( ),棱数( )之间存在一个有趣的数量关系: ,这就是著名的欧拉定理.某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形拼接而成,且有24个顶点,每个顶点都有3条棱,设该多面体外表面三角形个数是 个,八边形的个数是 ,则x+y= .三、解答题
-
14. 如图是一个正方体的表面展开图,每一个面上都写有一个整数,并且相对两个面上所写的两个互为相反数,求的值.
 15. 如图,是一个几何体的表面展开图,依据图中数据求该几何体的表面积和体积.
15. 如图,是一个几何体的表面展开图,依据图中数据求该几何体的表面积和体积.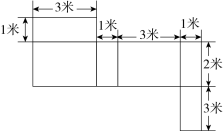
四、作图题
-
16. 图1所示的三棱柱,高为8cm,底面是一个边长为5cm的等边三角形.
 (1)、这个三棱柱有条棱,有个面;(2)、图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);(3)、要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开条棱,需剪开棱的棱长的和的最大值为cm.
(1)、这个三棱柱有条棱,有个面;(2)、图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);(3)、要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开条棱,需剪开棱的棱长的和的最大值为cm.五、综合题
-
17. 如图1,现有一个棱长为20cm的立方体水槽放在桌面上,水槽内水的高度为acm,往水槽里放入棱长为10cm的立方体铁块.
 (1)、求下列两种情况下a的值.
(1)、求下列两种情况下a的值.①若放入铁块后水面恰好在铁块的上表面,则a=cm;②若放入铁块后水槽恰好盛满(无溢出),则a=cm;
(2)、若0≤a≤7.5,放入铁块后水槽内水面的高度为cm,(用含a的代数式表示).(3)、如图2,在水槽旁用管子连通一个底面在桌面上的圆柱形容器,内部底面积为50cm2 , 管口底部A离水槽内底面的高度为hcm (h>a),水槽内放入铁块,水溢入圆柱形容器后,容器内水面与水槽内水面的高度差为4cm,若 a=15,求h的值.(水槽和容器的壁及底面厚度相同)
18. 在一次青少年模型大赛中,小高和小刘各制作了一个模型,小高制作的是棱长为acm的正方体模型,小刘制作的是棱长为acm的正方体右上角割去一个长为3cm,宽为2cm,高为1cm的长方体模型(如图2) (1)、用含a的代数式表示,小高制作的模型的各棱长度之和是;(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 ,求a的值;(3)、在(2)的条件下,
(1)、用含a的代数式表示,小高制作的模型的各棱长度之和是;(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 ,求a的值;(3)、在(2)的条件下,①图3是小刘制作的模型中正方体六个面的展开图,图中缺失的有一部分已经很用阴影表示,请你用阴影表示出其余缺失部分,并标出边的长度.
②如果把小刘的模型中正方体的六个面展开,则展开图的周长是 ▲ cm;请你在图方格中画出小刘的模型中正方体六个面的展开图周长最大时的图形.

-