【北师大版】2023-2024学年数学七年级(上)期末仿真模拟试题(三)
试卷更新日期:2023-12-15 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列计算结果是负数的是( ) .A、 B、 C、 D、2. 神舟十五号载人飞船于2022年11月29日成功发射,载人飞船与空间站组合体对接后,在距离地球表面约430000米左右的轨道上运行.430000米用科学记数法表示是( ).A、米 B、米 C、米 D、米3. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、
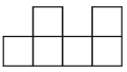 B、
B、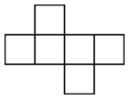 C、
C、 D、
D、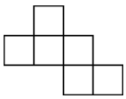 4. 已知 , 则的值为( )A、-4 B、0 C、4 D、-85. 下列各式中,正确的是( ) .A、 B、 C、 D、6. 下列说法正确的是( )A、两点之间的连线中,直线最短 B、若P是线段AB的中点,则AP=BP C、若AP=BP,则P是线段AB的中点 D、两点之间的线段叫做这两点之间的距离7. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒),若点P在运动过程中,当PB=2时,则运动时间t的值为( )
4. 已知 , 则的值为( )A、-4 B、0 C、4 D、-85. 下列各式中,正确的是( ) .A、 B、 C、 D、6. 下列说法正确的是( )A、两点之间的连线中,直线最短 B、若P是线段AB的中点,则AP=BP C、若AP=BP,则P是线段AB的中点 D、两点之间的线段叫做这两点之间的距离7. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒),若点P在运动过程中,当PB=2时,则运动时间t的值为( )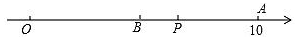 A、秒或秒 B、秒或秒或秒秒 C、3秒或7秒或或秒 D、秒或秒或秒秒8. 若关于x的一元一次方程的解,比关于x的一元一次方程﹣2(3x﹣4m)=1﹣5(x﹣m)的解大15,则m=( )A、2 B、1 C、0 D、﹣19. 如图,点C把线段AB从左至右依次分成2:3两部分,点D是AB的中点,若CD=2,则线段AB的长是( )
A、秒或秒 B、秒或秒或秒秒 C、3秒或7秒或或秒 D、秒或秒或秒秒8. 若关于x的一元一次方程的解,比关于x的一元一次方程﹣2(3x﹣4m)=1﹣5(x﹣m)的解大15,则m=( )A、2 B、1 C、0 D、﹣19. 如图,点C把线段AB从左至右依次分成2:3两部分,点D是AB的中点,若CD=2,则线段AB的长是( ) A、10 B、15 C、20 D、2510. 有理数 , , , 在数轴上的对应点的位置如图所示.则在下列选项中,正确的是( )
A、10 B、15 C、20 D、2510. 有理数 , , , 在数轴上的对应点的位置如图所示.则在下列选项中,正确的是( )
①如果 , 则一定会有;②如果 , 则一定会有;③如果 , 则一定会有;④如果 , 则一定会有 .
A、①④ B、①③ C、②③ D、②④二、填空题(每题3分,共15分)
-
11. 某地制作一年来每个月平均气温变化统计图,请你帮忙选择最恰当的统计图是 .(从条形统计图、折线统计图、扇形统计图中选一个)12. 如图,是用若干个边长为1的小正方体堆积而成的几何体,该几何体的左视图的面积为。
 13. 下午3:40,时针和分针的夹角是 .14. 如图所示,将一张长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕.若BD为∠A′BE的平分线,则∠CBD= .
13. 下午3:40,时针和分针的夹角是 .14. 如图所示,将一张长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕.若BD为∠A′BE的平分线,则∠CBD= .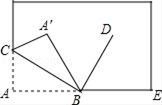 15. 如图是由六个不同颜色的正方形组成的长方形,已知中间最小的一个正方形A的边长为2,那么正方形B的面积是 .
15. 如图是由六个不同颜色的正方形组成的长方形,已知中间最小的一个正方形A的边长为2,那么正方形B的面积是 .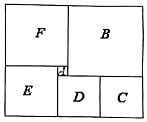
三、解答题(共7题,共55分)
-
16. 计算下列各式(1)、(2)、117.(1)、计算:(2)、合并同类项:18. 解方程:(1)、(2)、19. 观察下列两个等式: , , 给出定义如下:
我们称使等式成立的一对有理数 , 为“共生有理数对”,记为 , 如数对 , , 都是“共生有理数对”.
(1)、判断数对 , 是否为“共生有理数对”,并说明理由;(2)、若是“共生有理数对”,且 , 求的值;(3)、若是“共生有理数对”,则是“共生有理数对”吗?请说明理由.20. 某商店有两种书包,每个小书包比大书包的进价少10元,而它们的售后利润额相同.其中,每个小书包的盈利率为 , 每个大书包的盈利率为 , 试求两种书包的进价.21. 如图,已知数轴上两点A、B.点C为数轴上的动点,其表示的数为x. (1)、若点C到点A、B的距离相等,则点C表示的数x的值为;(2)、式子|x-3|+|x+1|的最小值是;(3)、点D也是数轴上的一个动点,已知点C的运动速度为每秒2个单位长度,动点C、D同时分别从点A、B出发开始运动.
(1)、若点C到点A、B的距离相等,则点C表示的数x的值为;(2)、式子|x-3|+|x+1|的最小值是;(3)、点D也是数轴上的一个动点,已知点C的运动速度为每秒2个单位长度,动点C、D同时分别从点A、B出发开始运动.①若点C、D相向而行,在表示数的点相遇,求点D的运动速度;
②若点D的运动速度是每秒4个单位长度,C、D两点同时向左匀速运动,则当C、D两点之间的距离为2时,两点运动了多长时间?
(4)、若动点C从点A出发,第一次向左运动1个单位长度,第二次向右运动2个单位长度,第三次向左运动3个单位长度,…,按此规律不断在数轴上做往复运动,当点C运动了n次时,直接用含n的代数式表示出点C所表示的有理数.22. 如图1,点O为直线上一点,过点O作射线 , 使 , 将一直角三角板的直角顶点放在点O处,一边在射线上,另一边在直线的下方.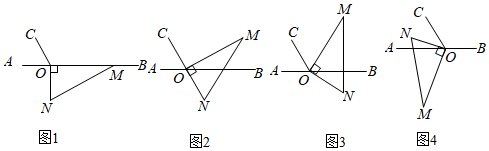 (1)、将图1中的三角板绕点O逆时针旋转至图2,使点N在的反向延长线上,请直接写出图中的度数;(2)、将图1中的三角板绕点O顺时针旋转至图3,使一边在的内部,且恰好平分 , 求的度数;(3)、将图1中的三角尺绕点O顺时针旋转至图4,使在内部,请探究与之间的数量关系,并说明理由.
(1)、将图1中的三角板绕点O逆时针旋转至图2,使点N在的反向延长线上,请直接写出图中的度数;(2)、将图1中的三角板绕点O顺时针旋转至图3,使一边在的内部,且恰好平分 , 求的度数;(3)、将图1中的三角尺绕点O顺时针旋转至图4,使在内部,请探究与之间的数量关系,并说明理由.