北师大版数学七年级上册期末冲刺满分攻略2 展开与折叠
试卷更新日期:2023-12-14 类型:复习试卷
一、选择题
-
1. ”磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )
 A、圆锥 B、长方体 C、五棱柱 D、圆柱2. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,现在原正方体中,与“一”字所在面相对的面上的汉字是( )
A、圆锥 B、长方体 C、五棱柱 D、圆柱2. 第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行,中国代表队自1982年新德里亚运会以来,连续蝉联金牌榜第一,中国已经成为亚洲体育第一强国.小明将“亚、洲、体、育、第、一”这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,现在原正方体中,与“一”字所在面相对的面上的汉字是( )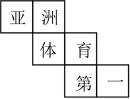 A、亚 B、洲 C、体 D、育3. 如图,将一个无盖正方体展开成平面图形的过程中,需要剪开____条棱.
A、亚 B、洲 C、体 D、育3. 如图,将一个无盖正方体展开成平面图形的过程中,需要剪开____条棱.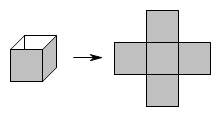 A、3 B、4 C、5 D、不确定4. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、
A、3 B、4 C、5 D、不确定4. 下面的平面图形均由六个边长相等的小正方形组成,经过折叠不能围成正方体的是( )A、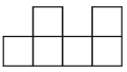 B、
B、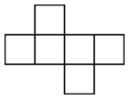 C、
C、 D、
D、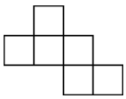 5. 某一长方体纸盒的表面展开图如图所示,根据图中数据可得该长方体纸盒的容积为:( )
5. 某一长方体纸盒的表面展开图如图所示,根据图中数据可得该长方体纸盒的容积为:( )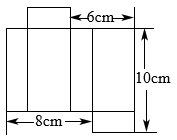 A、 B、 C、 D、6. 如图所示,是一个正方体纸盒的展开图,若在其中的三个正方形 , , 分别填入适当的数,使得它们折成正方体后相对面上的两个数互为相反数,则填入正方形 , , 的三个数依次为( )
A、 B、 C、 D、6. 如图所示,是一个正方体纸盒的展开图,若在其中的三个正方形 , , 分别填入适当的数,使得它们折成正方体后相对面上的两个数互为相反数,则填入正方形 , , 的三个数依次为( )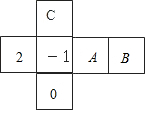 A、1,-2,0 B、-2,1,0 C、-2,0,1 D、0,-2,17. 下列结论,其中正确的为( )
A、1,-2,0 B、-2,1,0 C、-2,0,1 D、0,-2,17. 下列结论,其中正确的为( )①圆柱由3个面围成,这3个面都是平面 ②圆锥由2个面围成,这2个面中,1个是平的,1个不是平的 ③球仅由1个面围成,这1个面是平的 ④正方体由6个面围成,这6个面都是平的
A、①② B、②③ C、②④ D、③④8. 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )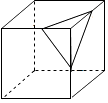 A、
A、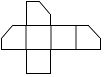 B、
B、 C、
C、 D、
D、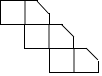 9.
9.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
 A、
A、 B、
B、 C、
C、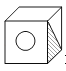 D、
D、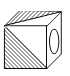 10.
10.用一个平面按如图所示的方式“切割”正方体,可以得到一个正方形的截面,将该正方体的侧面展开,“切割线”(虚线)位置正确的是( )
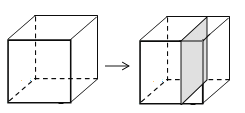 A、
A、 B、
B、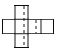 C、
C、 D、
D、
二、填空题
-
11. 如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号”一起向未来!”,那么在正方体的表面与”!”相对的汉字是。
 12. 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下面编号为1,2,3,6的小正方形中不能剪去的是(填编号).
12. 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下面编号为1,2,3,6的小正方形中不能剪去的是(填编号). 13. 如图是一个正方体形状纸盒的展开图,将其折成正方体后,相对面上的两数互为相反数,则 .
13. 如图是一个正方体形状纸盒的展开图,将其折成正方体后,相对面上的两数互为相反数,则 .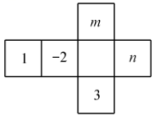 14.
14.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有 种拼接方法.
 15. 一个边长为4cm的正方形折叠围成一个四棱柱的侧面,若该四棱柱的底面是一个正方形,则此正方形边长为cm.16.
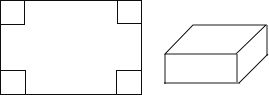
15. 一个边长为4cm的正方形折叠围成一个四棱柱的侧面,若该四棱柱的底面是一个正方形,则此正方形边长为cm.16.如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为 .
三、解答题
-
17. 李明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
 (1)、共有种弥补方法;(2)、任意画出一种成功的设计图在图中补充;(3)、在你帮忙设计成功的图中,要把 , , , , , 这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得直接在图中填上18. 如图是一个正方体盒子的展开图,要把﹣6、 、﹣1、6、﹣ 、1这些数字分别填入六个小正方形中,使得按虚线折成的正方体相对面上的两个数互为相反数.
(1)、共有种弥补方法;(2)、任意画出一种成功的设计图在图中补充;(3)、在你帮忙设计成功的图中,要把 , , , , , 这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得直接在图中填上18. 如图是一个正方体盒子的展开图,要把﹣6、 、﹣1、6、﹣ 、1这些数字分别填入六个小正方形中,使得按虚线折成的正方体相对面上的两个数互为相反数.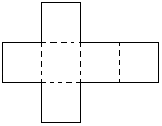 19.
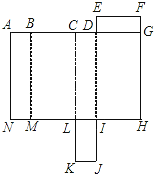
19.如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
 20.
20.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
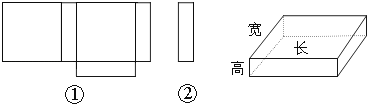
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
21.回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
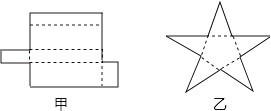
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
22. 如图所示是长方体的表面展开图,折叠成一个长方体,那么: (1)、与字母N重合的点是(2)、若AG=CK=14cm,FG=2cm,LK=5cm,则该长方体的表面积和体积分别是多少?23. 已知如图为一几何体从不同方向看到的图形.
(1)、与字母N重合的点是(2)、若AG=CK=14cm,FG=2cm,LK=5cm,则该长方体的表面积和体积分别是多少?23. 已知如图为一几何体从不同方向看到的图形. (1)、写出这个几何体的名称;(2)、任意画出这个几何体的一种表面展开图;(3)、若长方形的高为8厘米,三角形的边长为3厘米,求这个几何体的侧面积.24. 如图1,大正方体上截去一个小正方体后,可得到图2的几何体.
(1)、写出这个几何体的名称;(2)、任意画出这个几何体的一种表面展开图;(3)、若长方形的高为8厘米,三角形的边长为3厘米,求这个几何体的侧面积.24. 如图1,大正方体上截去一个小正方体后,可得到图2的几何体. (1)、设原大正方体的表面积为S,图2中几何体的表面积为S′,那么S′与S的大小关系是( )A、S′>S B、S′=S C、S′<S D、不确定(2)、小明说:“设图1中大正方体各棱的长度之和为c,图2中几何体各棱的长度之和为c′,那么c′比c正好多出大正方体3条棱的长度.”若设大正方体的棱长为1,小正方体的棱长为x,请问x为何值时,小明的说法才正确?(3)、如果截去的小正方体的棱长为大正方体棱长的一半,那么图3是图2中几何体的表面展开图吗?如有错误,请在图3中修正.
(1)、设原大正方体的表面积为S,图2中几何体的表面积为S′,那么S′与S的大小关系是( )A、S′>S B、S′=S C、S′<S D、不确定(2)、小明说:“设图1中大正方体各棱的长度之和为c,图2中几何体各棱的长度之和为c′,那么c′比c正好多出大正方体3条棱的长度.”若设大正方体的棱长为1,小正方体的棱长为x,请问x为何值时,小明的说法才正确?(3)、如果截去的小正方体的棱长为大正方体棱长的一半,那么图3是图2中几何体的表面展开图吗?如有错误,请在图3中修正.