【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略8 等腰三角形的性质与判定

试卷更新日期：2023-12-14 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知等腰三角形的一个内角是30°，那么这个等腰三角形顶角的度数是（）

A、75° B、120° C、30° D、30°或120°

查看试题解析
2. 等腰三角形的一边等于3，一边等于7，则此三角形的周长为（）

A、10 B、13 C、17 D、13或17

查看试题解析
3. 如图，△ABC中， $A B = A C$ ， D是BC的中点， $∠ B A C = 50 °$ ，则∠BAD的度数为（）

A、25° B、50° C、65° D、100°

查看试题解析
4. 如图，已知 $A B = A D ， A E = A C = B C ， ∠ 1 = ∠ 2 ， ∠ C = 40 °$ ，则 $∠ A D E$ 的度数为（）

A、 $40 °$ B、 $65 °$ C、 $70 °$ D、 $75 °$

查看试题解析
5. 下列命题的逆命题是假命题的是（）

A、两直线平行，同位角相等 B、线段垂直平分线上的点到线段两端距离相等 C、对顶角相等 D、等腰三角形两腰上的高线相等

查看试题解析
6. 等腰三角形的一个角是 $80 °$ ，则它的底角是（）

A、 $50 °$ B、 $80 °$ C、 $20 °$ 或 $80 °$ D、 $50 °$ 或 $80 °$

查看试题解析
7. △ABC中，AB=AC，CD为AB上的高，且△ADC为等腰三角形，则∠BCD等于（ )

A、 $67 . 5^{°}$ 或 $4 5^{°}$ B、 $22 . 5^{°}$ 或 $4 5^{°}$ C、 $3 6^{°}$ 或 $7 2^{°}$ D、 $67 . 5^{°}$ 或 $22 . 5^{°}$

查看试题解析
8. 如图，在△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB于E点，DF⊥AC于点F，则下列四个结论：①AD上任意一点到AB，AC两边的距离相等； ②AD⊥BC且BD＝CD；③∠BDE＝∠CDF；④AE＝AF.其中正确的有（）

A、②③ B、①③ C、①②④ D、①②③④

查看试题解析
9. 如图， $△ A O B ≌ △ A D C$ ， $∠ O ＝ ∠ D ＝ 90 °$ ，记 $∠ O A D ＝ α$ ， $∠ A B O ＝ β$ ，当 $B C ∥ O A$ 时，α与β之间的数量关系为（　　）

A、 $α ＝ β$ B、 $α ＝ 2 β$ C、 $α + β ＝ 90 °$ D、 $α + 2 β ＝ 180 °$

查看试题解析
10. 如图，在等腰三角形ABC中，AB＝AC＝4，∠BAC＝30°，AG是底边BC上的高.在AG的延长线上有一个动点D，连接CD，作∠CDE＝150°，交AB的延长线于点E，∠CDE的角平分线交AB边于点F，则在点D运动的过程中，线段EF的最小值（）

A、6 B、4 C、3 D、2

查看试题解析

二、填空题

11. 一张小凳子的结构如图所示，AC=BC，∠1=100°，则∠2=°．

查看试题解析
12. 若等腰三角形的两边长分别是4和6，则这个三角形的周长是.

查看试题解析
13. 在等腰三角形 $A B C$ 中，若 $∠ B = 140 °$ ，则 $A B$ $A C$ （用“＞”“＝”“＜”中的一个符号填空）.

查看试题解析
14. 如图所示的衣架可以近似看成一个等腰三角形ABC，其中 $A B = A C = 25 c m$ ，底边BC的长 $48 c m$ ，那么衣架的高 $A D =$ $c m$ .

查看试题解析
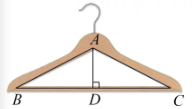15. 如图，在等腰△ABC中，AB=AC，∠A=36°，BD⊥AC于点D，则∠CBD= ．

查看试题解析
16. 小丽从一张等腰三角形纸片ABC（AB＝AC）中恰好剪出五个如图所示的小等腰三角形，其中BC＝BD，EC＝EF＝FG＝DG＝DA，则∠B＝°.

查看试题解析

三、解答题

17. 已知等腰三角形的一边长等于 $8 c m$ ，一边长等于 $9 c m$ ，求它的周长.

查看试题解析
18. 如图，已知 $A B = A C ， ∠ B = ∠ C$ ，则 $B D = C D$ ，请说明理由。

查看试题解析
19. 上午8时，一条船从海岛A出发，以15海里/时的速度向正北航行，10时到达海岛B处，从A，B望灯塔C，测得∠NAC=43°，∠NBC=86°，问海岛B与灯塔C相距多远？

查看试题解析
20. △ABC中，AB=AC，E为AC中点，F为BE上一点，且CE=CF．若△ABC的三条边长均为偶数，且BF与BE两条线段长度的乘积为20. 求△ABC的周长．

查看试题解析
21. 若 $a$ ， $b$ 是 $△ A B C$ 的两边，且 $| a - 3 | + (b - 4)^{2} = 0$ ．

(1)、试求 $a$ ， $b$ 的值，并求第三边 $c$ 的取值范围；

(2)、若 $△ A B C$ 是等腰三角形，试求此三角形的周长．

查看试题解析
22. 如图1，在平行四边形 $A B C D$ 中， $B E$ 平分 $∠ A B C$ 交 $C D$ 于点E， $C F ⊥ A D$ 于点F，交 $B E$ 于点G，且 $C F = C E$ ，连接 $E F$ .

(1)、求证： $C E = A D$ .

(2)、若 $A F = D E = 1$ ，求BC的长度；

(3)、在（2）的条件下，如图2，若 $C M$ 平分 $∠ D C F$ 交 $B E$ 于点M，求 $C M$ 的长.

查看试题解析
23. 定义：三角形一边上的点到三角形的另两条边的距离相等，称此点为这个三角形这边上的雅实心，如：
如图1，当点P在 $△ A B C$ 的 $A C$ 边上时，若 $P D ⊥ B C$ 于点D， $P E ⊥ A B$ 于点E，且 $P D = P E$ ，则称点P为 $△ A B C$ 的 $A C$ 边上的雅实心， $△ A B C$ 各边上的三个雅实心为顶点构成新三角形，叫做 $△ A B C$ 的雅实三角形.

(1)、如图2， $△ A B C$ 中， $A B = A C = 10 c m$ ， $B C = 12 c m$ ，求 $B C$ 边上的雅实心P到 $A B$ 的距离 $P D$ .

(2)、如图3，等边 $△ A B C$ 的边长为 $4 c m$ ，求等边 $△ A B C$ 的雅实三角形的面积.

(3)、如图4，在平面直角坐标系 $x O y$ 中，点A，B分别在x，y轴上，且 $A (2 ， 0)$ ， $∠ B A O = 60 °$ ，求 $△ A O B$ 的斜边上的雅实心P的坐标.

查看试题解析