【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略7 角平分线
试卷更新日期:2023-12-14 类型:复习试卷
一、选择题
-
1. 如图,OD平分于点是射线OB上的任一点,则DF的长度不可能是( )
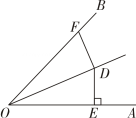 A、2.8 B、3 C、4.2 D、52. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、2.8 B、3 C、4.2 D、52. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )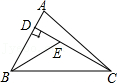 A、10 B、7 C、5 D、43. 如图,平分 , 于点 , 若 , 点是边上一动点,关于线段叙述正确的是( )
A、10 B、7 C、5 D、43. 如图,平分 , 于点 , 若 , 点是边上一动点,关于线段叙述正确的是( ) A、 B、 C、 D、4. 下列尺规作图,能判断AD是△ABC边上的中线的是( )A、
A、 B、 C、 D、4. 下列尺规作图,能判断AD是△ABC边上的中线的是( )A、 B、
B、 C、
C、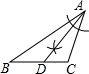 D、
D、 5. 如图,在中,平分交AC于点D,且 , F在BC上,E为AF的中点,连接DE,若 , , , 则AB的长为( )
5. 如图,在中,平分交AC于点D,且 , F在BC上,E为AF的中点,连接DE,若 , , , 则AB的长为( ) A、 B、 C、 D、96. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )
A、 B、 C、 D、96. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )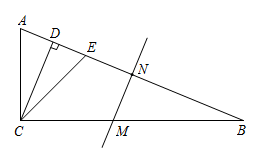 A、2 B、 C、 D、7. 如图、等腰三角形中, , 中线与角平分线交于点F,则的度数为( )
A、2 B、 C、 D、7. 如图、等腰三角形中, , 中线与角平分线交于点F,则的度数为( ) A、 B、 C、 D、8. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
A、 B、 C、 D、8. 如图,在中, , 是的高线,是的角平分线,则的度数是( )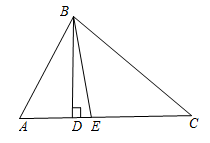 A、 B、 C、 D、9. 如图,在等腰三角形中, , , 是底边上的高,在的延长线上有一个动点D,连接 , 作 , 交的延长线于点E,的角平分线交边于点F,则在点D运动的过程中,线段的最小值( )
A、 B、 C、 D、9. 如图,在等腰三角形中, , , 是底边上的高,在的延长线上有一个动点D,连接 , 作 , 交的延长线于点E,的角平分线交边于点F,则在点D运动的过程中,线段的最小值( )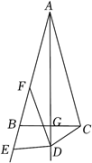 A、6 B、4 C、3 D、210. 如图, , 、、分别平分的外角、内角、外角以下结论:
A、6 B、4 C、3 D、210. 如图, , 、、分别平分的外角、内角、外角以下结论:
;;
;平分 .
其中正确的结论有( )
A、个 B、个 C、个 D、个二、填空题
-
11. 已知中, , 平分 , 平分 , 若 , 则的度数为.12. 如图,在中,平分交于点 , , 垂足为若 , , 则的面积为.
 13. 如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为.
13. 如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为. 14. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为.
14. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为. 15. 如图,在中, , , , 点D在上,过点D作的垂线,分别交射线 , 线段于点E,F,连接 , 恰好平分 , 则线段的长是.
15. 如图,在中, , , , 点D在上,过点D作的垂线,分别交射线 , 线段于点E,F,连接 , 恰好平分 , 则线段的长是. 16. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .
16. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .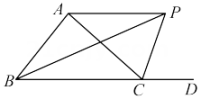
三、解答题
-
17. 如图,点和点在内部.请你作出点 , 使点到点和点的距离相等,且到两边的距离相等保留作图痕迹,不写作法;
 18. 已知,如图,在中, , 分别是的高和角平分线,若 , , 求的度数.
18. 已知,如图,在中, , 分别是的高和角平分线,若 , , 求的度数. 19. 如图,在中, , BD平分∠ABC,已知AD=3cm,BC=7cm,求的面积.
19. 如图,在中, , BD平分∠ABC,已知AD=3cm,BC=7cm,求的面积. 20. 如图,在中,是角平分线, , 分别为 , 上的点,且与有何数量关系请说明理由.
20. 如图,在中,是角平分线, , 分别为 , 上的点,且与有何数量关系请说明理由. 21. 如图,在中, , .
21. 如图,在中, , .
①分别以点A、B为圆心,以大于的长度为半径作弧,分别交于两点,连接这两点的直线与交于点D,与交于点F,连结;
②以点A为圆心,任意长为半径作弧,分别与、交于两点,再以这两点为圆心,以大于这两点间距离的一半的长度为半径作弧,两弧交于一点,连结点A与这一点交于点E.
(1)、通过以上作图,可以发现直线是 , 射线是;(在横线上填上合适的选项)A.线段的垂直平分线 B.的角平分线
C.的中线 D.的角平分线
(2)、在(1)所作的图中,求的度数.22. 如图,已知AD∥BC , ∠A=∠C=m°. (1)、如图①,求证:AB∥CD;(2)、如图②,连结BD,若点E在AB上,且满足∠FDB=∠BDC,并且DE平分∠ADF,求∠EBD的度数(用含m的代数式表示).(3)、如图③,在(2)的条件下,将线段BC沿着射线AB的方向向右平移,求∠ABD的度数.(用含m的代数式表示)23. 概念学习
(1)、如图①,求证:AB∥CD;(2)、如图②,连结BD,若点E在AB上,且满足∠FDB=∠BDC,并且DE平分∠ADF,求∠EBD的度数(用含m的代数式表示).(3)、如图③,在(2)的条件下,将线段BC沿着射线AB的方向向右平移,求∠ABD的度数.(用含m的代数式表示)23. 概念学习规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
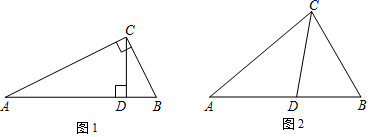
从三角形不是等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
 (1)、理解概念
(1)、理解概念
如图1,在中, , , 请写出图中两对“等角三角形”(2)、概念应用
如图2,在中,为角平分线, , .求证:为的等角分割线.
(3)、在中, , 是的等角分割线,直接写出的度数.