【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略6 线段垂直平分线
试卷更新日期:2023-12-14 类型:复习试卷
一、选择题
-
1. 如图,直线CD是线段AB的垂直平分线,Р为直线CD上的一点.已知△PAB的周长为14,PA=4,则线段AB的长度为( )
 A、6 B、5 C、4 D、32. 如图,在中,分别以 , 为圆心,大于线段长度一半的长为半径作弧,相交于点 , , 连结 , 交于点若 , , 则的周长为( )
A、6 B、5 C、4 D、32. 如图,在中,分别以 , 为圆心,大于线段长度一半的长为半径作弧,相交于点 , , 连结 , 交于点若 , , 则的周长为( ) A、6 B、8 C、10 D、143. 如图,在中, , 垂直平分 , 垂足为 , 交于 , 若 , 则的周长为( )
A、6 B、8 C、10 D、143. 如图,在中, , 垂直平分 , 垂足为 , 交于 , 若 , 则的周长为( ) A、 B、 C、 D、4. 如图,中, , 平分 , , , 则的面积为( )
A、 B、 C、 D、4. 如图,中, , 平分 , , , 则的面积为( ) A、15 B、10 C、15 D、305. 如图,在中, , 边AC的垂直平分线DE交AB于点 , 交AC于点 , 财AC的长为( )
A、15 B、10 C、15 D、305. 如图,在中, , 边AC的垂直平分线DE交AB于点 , 交AC于点 , 财AC的长为( ) A、6 B、 C、9 D、6. 如图,在中,是的垂直平分线,连接 . 以A为圆心,任意长为半径画弧,分别交于点E,F,分别以E,F为圆心,以大于长为半径画弧,两圆弧交于G点,作射线交于点H,则的度数为( )
A、6 B、 C、9 D、6. 如图,在中,是的垂直平分线,连接 . 以A为圆心,任意长为半径画弧,分别交于点E,F,分别以E,F为圆心,以大于长为半径画弧,两圆弧交于G点,作射线交于点H,则的度数为( ) A、36° B、25° C、24° D、21°7. 有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应该挖在( )
A、36° B、25° C、24° D、21°7. 有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应该挖在( ) A、三条角平分线的交点处 B、三条中垂线的交点处 C、三条高线所在直线的交点处 D、三条中线的交点处8. 如图,中,的垂直平分线交AB于点 , 交BC于点E,AC的垂直平分线交AC于点F,交BC于点.若以BE,EG,GC为边的三角形的面积为8,则的面积可能是( )
A、三条角平分线的交点处 B、三条中垂线的交点处 C、三条高线所在直线的交点处 D、三条中线的交点处8. 如图,中,的垂直平分线交AB于点 , 交BC于点E,AC的垂直平分线交AC于点F,交BC于点.若以BE,EG,GC为边的三角形的面积为8,则的面积可能是( ) A、12 B、14 C、16 D、189. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( )
A、12 B、14 C、16 D、189. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( ) A、1: B、1:2 C、1: D、1:10. 如图,直角三角形ABC中,AC=BC,AD是△ABC的角平分线,动点M、N同时从A点出发,以相同的速度分别沿A→C→B和A一B→C方向运动,并在边BC上的点E相遇,连接AE,①AE平分△ABC的周长,②AE是△ABD的角平分线,③AE是△ABD的中线.以上结论正确的有( )
A、1: B、1:2 C、1: D、1:10. 如图,直角三角形ABC中,AC=BC,AD是△ABC的角平分线,动点M、N同时从A点出发,以相同的速度分别沿A→C→B和A一B→C方向运动,并在边BC上的点E相遇,连接AE,①AE平分△ABC的周长,②AE是△ABD的角平分线,③AE是△ABD的中线.以上结论正确的有( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 线段的垂直平分线上的点与这条线段的的距离相等.12. 如图,在 中, ,线段 的垂直平分线交 于点 , ,则 的长为.
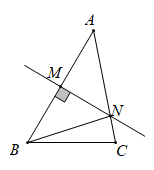 13. 如图,在中,直线是边的垂直平分线,连接 , 若 , 则的周长为.
13. 如图,在中,直线是边的垂直平分线,连接 , 若 , 则的周长为. 14. 如图,DE,FG分别是AB,AC的垂直平分线.若 的周长为15,则 .
14. 如图,DE,FG分别是AB,AC的垂直平分线.若 的周长为15,则 . 15. 如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OD的垂直平分线交OA、OB分别于点P,Q,点E是OA上异于点P的一点,且DE=OP=6,则△ODE的面积为.
15. 如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OD的垂直平分线交OA、OB分别于点P,Q,点E是OA上异于点P的一点,且DE=OP=6,则△ODE的面积为. 16. 如图,在△ABC中,AB=AC=4,∠BAC=120°,M是BC的中点,点E是AB边上的动点,点F是线段BM上的动点,则ME+EF的最小值等于.
16. 如图,在△ABC中,AB=AC=4,∠BAC=120°,M是BC的中点,点E是AB边上的动点,点F是线段BM上的动点,则ME+EF的最小值等于.
三、解答题
-
17. 如图所示,已知 , 用直尺和圆规作:(保留作图痕迹,不要求写作法)

①∠C的角平分线CE;
②BC边上的中线AF.
18. 如图,在△ABC中,点E在AB边上,请用直尺和圆规求作一点F,使得FE=FA,且F点到AB和BC的距离相等.(保留作图痕迹,不写作法) 19. 如图,直线m表示一条公路,A,B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.请用尺规在图上找出点P并说明理由.
19. 如图,直线m表示一条公路,A,B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.请用尺规在图上找出点P并说明理由.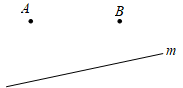 20. 如图,在 中, 是 的中垂线,分别交 , 于点D,E.若 的周长为8, ,求 的长.
20. 如图,在 中, 是 的中垂线,分别交 , 于点D,E.若 的周长为8, ,求 的长. 21. 如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由:
21. 如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由: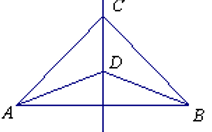
解:∵ CD是线段AB的垂直平分线
∴ AC=BC,AD=DB( )
在△ADC和△BDC中,
 ( )
( )∴△ADC≌和△BDC( ).
∴ ∠CAD=∠CBD( ).
22. 思维启迪: (1)、如图1,点P是线段 , 的中点,则与的数量关系为 , 位置关系为 ;(2)、思维探索:
(1)、如图1,点P是线段 , 的中点,则与的数量关系为 , 位置关系为 ;(2)、思维探索:
①如图2,在中, , 点D为内一点,连接 , , 延长到点E , 使 , 连接 , 若 , 请用等式表示 , , 之间的数量关系,并说明理由;②如图3,在中, , , 点D为中点,点E在线段上(点E不与点B , 点D重合),连接 , 过点A作 , 连接.若 , , 请直接写出的长.
23. 如图, , 射线 , 且 , 点是线段不与点、重合上的动点,过点作交射线于点 , 连接. (1)、如图1,若 , , 求的长.(2)、如图2,若平分 ,
(1)、如图1,若 , , 求的长.(2)、如图2,若平分 ,试猜测和的数量关系,并说明理由;
若的面积为5,求四边形的面积.
(3)、如图3,①已知点是网格中的格点,若三角形是以为底边的等腰三角形,那么这样的点共有 ▲ 个;
②在网格中找出一个点 , 使得点到点 , 和点 , 的距离分别相等,请在网格中标注点保留作图痕迹