【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略4 尺规作图
试卷更新日期:2023-12-14 类型:复习试卷
一、选择题
-
1. 如图,观察图中的尺规作图痕迹,下列说法错误的是( )
 A、 B、 C、 D、2. 尺规作图作的平分线的方法如下:
A、 B、 C、 D、2. 尺规作图作的平分线的方法如下:如图,以点为圆心,任意长为半径作弧,交 , 于点 , , 再分别以点 , 为圆心,以大于长为半径作弧,两弧交于点 , 作射线由作法得到的根据是.( )
 A、 B、 C、 D、3. 如图,在中,是的垂直平分线,连接 . 以A为圆心,任意长为半径画弧,分别交于点E,F,分别以E,F为圆心,以大于长为半径画弧,两圆弧交于G点,作射线交于点H,则的度数为( )
A、 B、 C、 D、3. 如图,在中,是的垂直平分线,连接 . 以A为圆心,任意长为半径画弧,分别交于点E,F,分别以E,F为圆心,以大于长为半径画弧,两圆弧交于G点,作射线交于点H,则的度数为( ) A、36° B、25° C、24° D、21°4. 如图,在Rt△ABC中,观察作图痕迹,若BF=2,则CF的长为( )
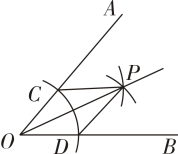
A、36° B、25° C、24° D、21°4. 如图,在Rt△ABC中,观察作图痕迹,若BF=2,则CF的长为( ) A、 B、3 C、2 D、5. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、
A、 B、3 C、2 D、5. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、 B、
B、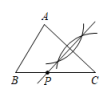 C、
C、 D、
D、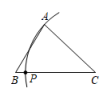 6. 如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若与的周长之差为4,则AE的长为( )
6. 如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若与的周长之差为4,则AE的长为( )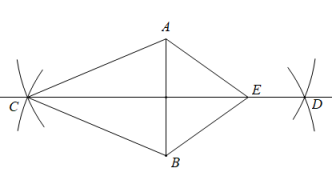 A、1 B、2 C、3 D、47. 如图,在 中, 用直尺和圆规在边BC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )A、
A、1 B、2 C、3 D、47. 如图,在 中, 用直尺和圆规在边BC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在△ABC中,分别以点A和B为圆心,大于 和长为半径画弧, 两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ABC的周长为17,AB=7,则△ADC的周长是 ( )
8. 如图,在△ABC中,分别以点A和B为圆心,大于 和长为半径画弧, 两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ABC的周长为17,AB=7,则△ADC的周长是 ( ) A、7 B、10 C、15 D、179. 如图 , 已知线段 , , 求作 , 使 , , 张蕾的作法如图所示,则下列说法中一定正确的是( )
A、7 B、10 C、15 D、179. 如图 , 已知线段 , , 求作 , 使 , , 张蕾的作法如图所示,则下列说法中一定正确的是( ) A、作的依据为 B、弧是以长为半径画的 C、弧是以点位圆心,为半径画的 D、弧是以长为半径画的10. 如图,依据尺规作图的痕迹,计算∠α=( )
A、作的依据为 B、弧是以长为半径画的 C、弧是以点位圆心,为半径画的 D、弧是以长为半径画的10. 如图,依据尺规作图的痕迹,计算∠α=( ) A、68° B、56° C、28° D、34°
A、68° B、56° C、28° D、34°二、填空题
-
11. 如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 .
 12. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.
12. 如图,在中, , 的垂直平分线交于M , 交于E , 的垂直平分线交于N , 交于F , 则的周长为 cm.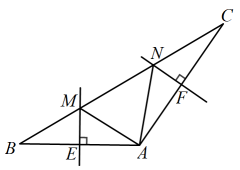 13. 如图,在平面直角坐标系中,根据尺规作图的痕迹在第二象限内作出点 , 则与的数量关系是 .
13. 如图,在平面直角坐标系中,根据尺规作图的痕迹在第二象限内作出点 , 则与的数量关系是 .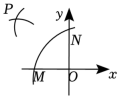 14. 如图,在Rt△BC中,∠C=90°。以顶点B为圆心、BC长为半径作圆弧,交AB于点D,再分别以点C和点D为圆心、大于CD长为半径作圆弧,两弧交于点E.作射线BE交AC于点F.若BC=12,AB=15,△BCF的面积为24.则△ABC的面积为
14. 如图,在Rt△BC中,∠C=90°。以顶点B为圆心、BC长为半径作圆弧,交AB于点D,再分别以点C和点D为圆心、大于CD长为半径作圆弧,两弧交于点E.作射线BE交AC于点F.若BC=12,AB=15,△BCF的面积为24.则△ABC的面积为 15. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.
15. 如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出个.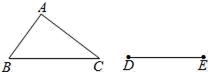 16. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为
16. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为
三、解答题
-
17. 已知:线段a,∠α.
求作:△ABC,使AB=BC=a,∠B=∠α.
 18. 如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
18. 如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:①以点A为圆心,小于AC的长为半径.画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于EF的长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D,求∠ADC的度数为
 19. 两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号反射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1 , l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
19. 两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号反射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1 , l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)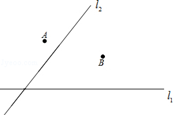 20. 如图,在△ABC中,∠C=90°,∠B=30°.
20. 如图,在△ABC中,∠C=90°,∠B=30°.(1)作∠A的平分线AD,交BC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加黑);
(2)计算S△DAC:S△ABC的值.
 21. 已知:两边及其夹角,线段 , , .
21. 已知:两边及其夹角,线段 , , .求作: ,使 , ,(用尺规作图,保留作图痕迹,不写作法).
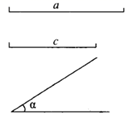
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的 是唯一的,依据是三角形全等判定定理中的_▲_.
22. 如图,在Rt△ABC中,∠C=90°,AC<BC.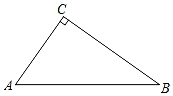 (1)、动手操作:要求尺规作图,不写作法,但保留作图痕迹.
(1)、动手操作:要求尺规作图,不写作法,但保留作图痕迹.①作出AB的垂直平分线MN,MN分别与AB交于点D,与BC交于点E.
②过点B作BF垂直于AE,垂足为F.
(2)、推理证明:求证AC=BF.23. 解决下列两个问题: (1)、如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;
(1)、如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;解:PA+PB的最小值为 .
(2)、如图2.点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)