【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略3 全等三角形的性质与判定

试卷更新日期：2023-12-14 类型：复习试卷

进入出卷网下载

一、选择题

1. 用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC＝∠BOC的依据是（）

A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等

查看试题解析
2. 如图， $△ A B C ≌ △ A D C$ ，若 $∠ B = 25 °$ ，则 $∠ D$ 的度数为（）

A、20° B、25° C、30° D、50°

查看试题解析
3. 如图，已知 $∠ 1 = ∠ 2$ ，要说明 $△ A B D ≅ △ A C D$ ，还需从下列条件中选一个，错误的选法是（）

A、 $D B = D C$ B、 $A B = A C$ C、 $∠ A D B = ∠ A D C$ D、 $∠ B = ∠ C$

查看试题解析
4. 下列命题属于假命题的是（）

A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等

查看试题解析
5. 已知△ABC≌△DEF，如果△DEF的周长为4，则△ABC的周长为（）

A、8 B、6 C、4 D、2

查看试题解析
6. 如图，已知 $∠ 1 = ∠ 2$ ，补充下列哪一个条件，仍不能判定 $△ ABD$ 和 $△ ACD$ 全等的是（）

A、 $∠ BAD = ∠ CAD$ B、 $∠ B = ∠ C$ C、 $BD = CD$ D、 $AB = AC$

查看试题解析
7.
如图，OA=OB，OC=OD，∠O=50°，∠D=35°，则∠AEC等于（）

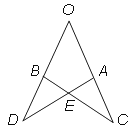A、60° B、50° C、45° D、30°

查看试题解析
8. 如图，用直尺和圆规作已知角的平分线的示意图，则说明∠CAD＝∠DAB的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
9. △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）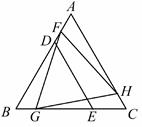

A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长

查看试题解析
10. 如图，AB＝AD，∠BAD＝140°，AB⊥CB于点B，AD⊥CD于点D，E、F分别是CB、CD上的点，且∠EAF＝70°，下列结论中①DF＝BE，②△ADF≌△ABE，③FA平分∠DFE，④EF平分∠AEC，⑤BE+DF＝EF．其中正确的结论是（）

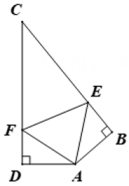A、④⑤ B、①② C、③⑤ D、①②③

查看试题解析

二、填空题

11. 如图，已知 $∠ A = ∠ D$ ，要使 $△ A B C ≌ △ D C B$ ，还需添加一个条件，这个条件可以是.

查看试题解析
12. 如图， $D$ 为 $R t △ A B C$ 中斜边 $B C$ 上的一点，且 $B D = A B$ ，过点 $D$ 作 $B C$ 的垂线，交 $A C$ 于点 $E$ ，若 $A E = 6 c m$ ， $D C = 8 c m$ ，则 $C E =$ $c m$ .

查看试题解析
13. 如图，△ABC≌△DEF，BC＝7，EC＝4，则CF的长为．

查看试题解析
14. 如图，在△ABC中，AB=AC，AD⊥BC于D点，E、F分别为DB、DC的中点，则图中共有全等三角形对．

查看试题解析
15. 如图， $A C = B C$ ， $D C = E C ， ∠ A C B = ∠ E C D = 90 °$ ，且 $∠ E B D = 50 °$ ，则 $∠ A E B =$ .

查看试题解析
16. 如图，已知 $A B ∥ C F$ ， E为 $D F$ 的中点，若 $A B = 8 c m$ ， $C F = 5 c m$ ，则 $B D =$ $c m$ ．

查看试题解析

三、解答题

17. 如图，已知在△ABC和△DBE中，AB＝DB，∠1＝∠2，∠A＝∠D．求证：BC＝BE．

查看试题解析
18. 如图，在 $△ A B C$ 和 $△ D E F$ 中，点 $B$ ， $F$ ， $C$ ， $E$ 在同一直线上， $A B = D E$ ， $B F = C E$ ， $A C = D F$ ，求证： $△ A B C$ ≌ $△ D E F$ .

查看试题解析
19. 如图，在△ABC和△ADC中，AB＝AD，BC＝DC，∠B＝140°，求∠D的度数．

查看试题解析
20. 莆仙戏是现存最古老的地方戏剧种之一，被称为“宋元南戏的活化石”，2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”．该剧中“油纸伞”无疑是最重要的道具，依伞设戏，情节新颖，结构巧妙，谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌．“油纸伞”的制作工艺十分巧妙．如图，伞圈D沿着伞柄滑动时，总有伞骨BD＝CD，AB＝AC，从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC．为什么？

查看试题解析
21. 如图，已知 $△ A B C$ 和 $△ A D E$ ， $A B = A D$ ， $∠ B A D = ∠ C A E$ ， $∠ B = ∠ D$ ， AD与BC交于点P，点C在DE上．

(1)、求证： $B C = D E$ ；

(2)、若 $∠ B = 30 °$ ， $∠ A P C = 70 °$ ，求∠E的度数．

查看试题解析
22. 如图，在四边形 $A B C D$ 中，P为 $C D$ 边上的一点， $B C ∥ A D$ . $A P$ 、 $B P$ 分别是 $∠ B A D$ 、 $∠ A B C$ 的角平分线.

(1)、若 $∠ B A D = 70 °$ ，则 $∠ A B P$ 的度数为， $∠ A P B$ 的度数为；

(2)、求证： $A B = B C + A D$ ；

(3)、设 $B P = 3 a$ ， $A P = 4 a$ ，过点P作一条直线，分别与 $A D$ ， $B C$ 所在直线交于点E、F，若 $A B = E F$ ，直接写出 $A E$ 的长（用含a的代数式表示）

查看试题解析
23. 如图，点A在直线l上，在直线l右侧做等腰三角形 $A B C$ ， $A B = A C$ ， $∠ B A C = α$ ，点D与点B关于直线l轴对称，连接 $C D$ 交直线l于点E，连接 $B E$ .

(1)、求证： $∠ A D C = ∠ A C D$ ；

(2)、求证： $∠ B E C = α$ ；

(3)、当 $α = 90 °$ 时，求证： $E D^{2} + C E^{2} = 2 A B^{2}$ .

查看试题解析