浙教版数学七年级上册期末冲刺满分攻略17 余角和补角
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 已知的余角为35°,则的补角度数是( )A、 B、 C、 D、2. 如图,点O在直线AB上,∠AOC=∠BOD=20°,则图中互补的角的对数是( )
 A、1对 B、2对 C、3对 D、4对3. 下列说法中,正确的是( )A、两点之间直线最短 B、如果∠α=53°38',那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小 D、相等的角是对顶角4. 已知 与 满足 ,下列式子表示的角:① :② ;③ ;④ 中,其中是 的余角的是( )A、①② B、①③ C、②④ D、③④5. 将一副三角板按下列图示位置摆放,其中的是( )A、
A、1对 B、2对 C、3对 D、4对3. 下列说法中,正确的是( )A、两点之间直线最短 B、如果∠α=53°38',那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小 D、相等的角是对顶角4. 已知 与 满足 ,下列式子表示的角:① :② ;③ ;④ 中,其中是 的余角的是( )A、①② B、①③ C、②④ D、③④5. 将一副三角板按下列图示位置摆放,其中的是( )A、 B、
B、 C、
C、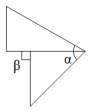 D、
D、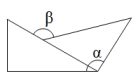 6. 如图,点在直线上,射线 , 在直线的同一侧(其中 , ),射线平分 , 射线平分 . 若和互补,则( )
6. 如图,点在直线上,射线 , 在直线的同一侧(其中 , ),射线平分 , 射线平分 . 若和互补,则( )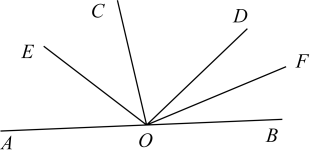 A、 B、 C、 D、7.
A、 B、 C、 D、7.如图,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2.其推理依据是( )
 A、同角的余角相等 B、等角的余角相等 C、同角的补角相等 D、等角的补角相等8.
A、同角的余角相等 B、等角的余角相等 C、同角的补角相等 D、等角的补角相等8.如图所示,一艘船从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC的余角是( )
 A、15° B、30° C、45° D、75°9.
A、15° B、30° C、45° D、75°9.在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
 A、
A、 B、
B、 C、
C、 D、
D、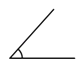 10.
10.如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知 , 则的补角的度数为.12. 已知∠α=47°30′,则∠α的余角的度数为°.13. 已知与互余,且 , 则的补角是度.14. 如果一个角的补角是 ,那么这个角的度数是.15. 一个角的补角加上10°后,等于这个角的余角的3倍,则这个角= °.16. 若 与 互为补角, , ,且 ,则 的余角的度数是度.(结果用同时含m , n的代数式表示)
三、解答题
-
17. 已知点直线BC及直线外一点A(如图),按要求完成下列问题:
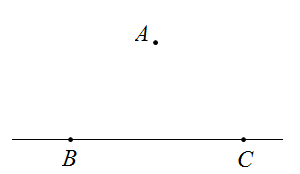 (1)、画出射线CA、线段AB.过C点画CD⊥AB,垂足为点D;(2)、比较线段CD和线段CA的大小,并说明理由;(3)、在以上的图中,互余的角为 , 互补的角为.(各写出一对即可)18. 如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
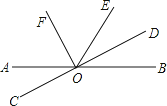
(1)、画出射线CA、线段AB.过C点画CD⊥AB,垂足为点D;(2)、比较线段CD和线段CA的大小,并说明理由;(3)、在以上的图中,互余的角为 , 互补的角为.(各写出一对即可)18. 如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
 19. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
19. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.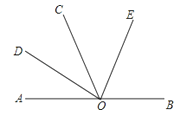 (1)、与∠AOE互补的角是(2)、若∠AOD=36°,求∠DOE的度数(3)、当∠AOD=x°时,请直接写出∠DOE的度数.20. 如图,直线 , 相交于点 , 和 互余, .
(1)、与∠AOE互补的角是(2)、若∠AOD=36°,求∠DOE的度数(3)、当∠AOD=x°时,请直接写出∠DOE的度数.20. 如图,直线 , 相交于点 , 和 互余, .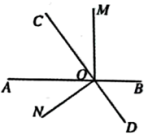 (1)、求 的度数;(2)、若 ,求 的度数.21.
(1)、求 的度数;(2)、若 ,求 的度数.21.如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,画出表示渔船D方向的射线OD,则渔船D在货轮O的方位角
 22. 将直角三角板OMN的直角顶点О放在直线AB上,射线OC平分∠AON.
22. 将直角三角板OMN的直角顶点О放在直线AB上,射线OC平分∠AON.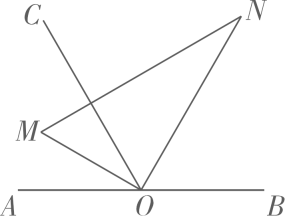 (1)、如图,若∠BON=60°,求∠COM的度数;(2)、将直角三角板OMN绕顶点О按逆时针方向旋转,在旋转过程中:
(1)、如图,若∠BON=60°,求∠COM的度数;(2)、将直角三角板OMN绕顶点О按逆时针方向旋转,在旋转过程中:①当∠BON=140°时,求∠COM的度数:
②直接写出∠BON和∠COM之间的数量关系.
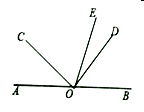
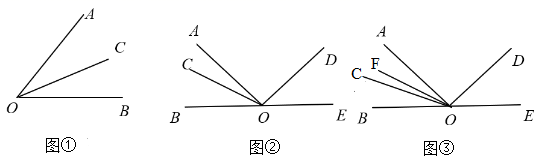 例如:图①中,当 时, 与 互余,那么 是 的余分线, 是 的余分角.
例如:图①中,当 时, 与 互余,那么 是 的余分线, 是 的余分角.