浙教版数学七年级上册期末冲刺满分攻略16 角
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 若 , , 则与的大小关系是( )A、 B、 C、 D、无法判断2. 如图,点为直线上一点,平分 , , 若 , 则的度数为( )
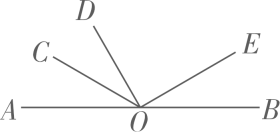 A、 B、 C、 D、3. 下列说法正确的是( )A、非负数就是指一切正数 B、数轴上任意一点都对应一个实数 C、两个锐角的和一定大于直角 D、一条直线就是一个平角4. 下列说法中,正确的是( )A、一根绳子,不用任何工具,可以找到它的中点 B、一条直线就是一个平角 C、若 ,则点B是线段AC的中点 D、两个锐角的度数和一定大于5. 如图是用尺规作∠AOB的平分线OC的示意图,这样作图的依据是( )
A、 B、 C、 D、3. 下列说法正确的是( )A、非负数就是指一切正数 B、数轴上任意一点都对应一个实数 C、两个锐角的和一定大于直角 D、一条直线就是一个平角4. 下列说法中,正确的是( )A、一根绳子,不用任何工具,可以找到它的中点 B、一条直线就是一个平角 C、若 ,则点B是线段AC的中点 D、两个锐角的度数和一定大于5. 如图是用尺规作∠AOB的平分线OC的示意图,这样作图的依据是( ) A、SAS B、SSS C、ASA D、AAS6. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定相等的是( )A、
A、SAS B、SSS C、ASA D、AAS6. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定相等的是( )A、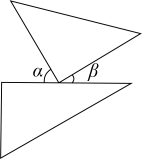 B、
B、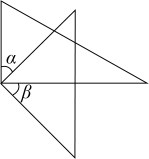 C、
C、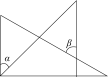 D、
D、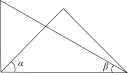 7. 如图, ,4位同学观察图形后各自观点如下.甲: ;乙: ;丙: ;丁:图中小于平角的角有6个;其中正确的结论是( )
7. 如图, ,4位同学观察图形后各自观点如下.甲: ;乙: ;丙: ;丁:图中小于平角的角有6个;其中正确的结论是( ) A、甲、乙、丙 B、甲、乙、丁 C、乙、丙、丁 D、甲、丙、丁8. 如图,点在直线上,射线 , 在直线的同一侧(其中 , ),射线平分 , 射线平分 . 若和互补,则( )
A、甲、乙、丙 B、甲、乙、丁 C、乙、丙、丁 D、甲、丙、丁8. 如图,点在直线上,射线 , 在直线的同一侧(其中 , ),射线平分 , 射线平分 . 若和互补,则( )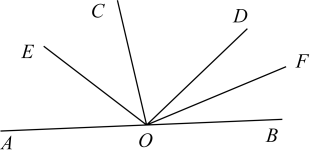 A、 B、 C、 D、9. 一个角的度数是42°46′,则它的余角的度数为( )A、47°14′ B、47°54′ C、57°14′ D、37°54′10. 如图,三条直线相交于点O,则∠1+∠2+∠3的度数等于( )
A、 B、 C、 D、9. 一个角的度数是42°46′,则它的余角的度数为( )A、47°14′ B、47°54′ C、57°14′ D、37°54′10. 如图,三条直线相交于点O,则∠1+∠2+∠3的度数等于( )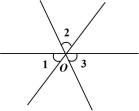 A、210° B、180° C、150° D、120°
A、210° B、180° C、150° D、120°二、填空题
-
11. 比较大小:32.5° 32°5'(填“>”、“=”或“<”).12. 已知与互余, , 则.13. 如图,将一副三角板摆成如图形状,如果 , 那么的度数是.
 14. 如图,已知 , 射线从出发,以每秒的速度在内部绕点逆时针旋转,若和中,有一个角是另一个角的2倍,则运动时间为秒.
14. 如图,已知 , 射线从出发,以每秒的速度在内部绕点逆时针旋转,若和中,有一个角是另一个角的2倍,则运动时间为秒.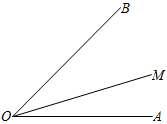 15. 如图, , 射线在内部, , 则度.
15. 如图, , 射线在内部, , 则度.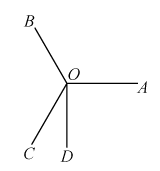 16. 如图,将量角器的中心与的顶点重合,读出射线OA,OB分别经过刻度18和140,把绕点O顺时针方向旋转到 , 读出的平分线OC经过刻度32,则的平分线经过的刻度是 .
16. 如图,将量角器的中心与的顶点重合,读出射线OA,OB分别经过刻度18和140,把绕点O顺时针方向旋转到 , 读出的平分线OC经过刻度32,则的平分线经过的刻度是 .
三、解答题
-
17. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 (结果用度表示).18. 如图,根据下列要求画图:
 (1)、画线段的中点D,并连结;(2)、过点A画的垂线段,垂足为E;(3)、画的平分线,交于点F.19. 如图1,OC平分∠AOB,OD是∠BOC内部从点O出发的一条射线,OE平分∠AOD.
(1)、画线段的中点D,并连结;(2)、过点A画的垂线段,垂足为E;(3)、画的平分线,交于点F.19. 如图1,OC平分∠AOB,OD是∠BOC内部从点O出发的一条射线,OE平分∠AOD.
 (1)、[基础尝试]
(1)、[基础尝试]如图2,若∠AOB=120°,∠COD=10°,求∠DOE的度数;
(2)、[画图探究]设∠COE=x°,用x的代数式表示∠BOD的度数;
(3)、[拓展运用]若∠COE与∠BOD互余,∠AOB与∠COD互补,求∠AOB的度数.
20. 如图,已知 , 射线在内部,射线绕点O逆时针旋转得到 , 是的角平分线. (1)、如图1,若是的角平分线,且时,求.
(1)、如图1,若是的角平分线,且时,求. (2)、如图2,若是的角平分线,则.(用含有n的代数式表示)
(2)、如图2,若是的角平分线,则.(用含有n的代数式表示) (3)、在(1)的条件下,若射线从出发绕点O以每秒5°的速度逆时针旋转,射线从出发绕点O以每秒6°的速度顺时针旋转.若射线、同时开始旋转,直至第一次重合,旋转停止.在旋转的过程中,何时满足 , 请直接写出答案.21. 如图1,已知点O在直线AB上,射线OD、OC分别在直线AB的上、下两侧且 , OE始终是的平分线.
(3)、在(1)的条件下,若射线从出发绕点O以每秒5°的速度逆时针旋转,射线从出发绕点O以每秒6°的速度顺时针旋转.若射线、同时开始旋转,直至第一次重合,旋转停止.在旋转的过程中,何时满足 , 请直接写出答案.21. 如图1,已知点O在直线AB上,射线OD、OC分别在直线AB的上、下两侧且 , OE始终是的平分线. (1)、若 , 求的度数.(2)、如图2,设 , 已知 , 求n的值.(3)、如图3,在满足(2)的条件下,射线OP从OB出发绕点O以每秒的速度逆时针旋转,射线OQ从OE出发绕点O以每秒的速度顺时针旋转,射线OP、OQ同时开始旋转,记旋转时间为t秒.当和互余时,求旋转时间t的值.22. 如图1所示是某款手表实物图,其示意图如图2所示,已知表盘是以O为圆心,以厘米为半径的圆,为圆的直径,其中时针为线段 , 分针为线段 , 且点A、B、O、C、D都在同一条直线上.
(1)、若 , 求的度数.(2)、如图2,设 , 已知 , 求n的值.(3)、如图3,在满足(2)的条件下,射线OP从OB出发绕点O以每秒的速度逆时针旋转,射线OQ从OE出发绕点O以每秒的速度顺时针旋转,射线OP、OQ同时开始旋转,记旋转时间为t秒.当和互余时,求旋转时间t的值.22. 如图1所示是某款手表实物图,其示意图如图2所示,已知表盘是以O为圆心,以厘米为半径的圆,为圆的直径,其中时针为线段 , 分针为线段 , 且点A、B、O、C、D都在同一条直线上. (1)、若点B,C是线段的三等分点,求表长.(2)、若手表显示是9点30分.
(1)、若点B,C是线段的三等分点,求表长.(2)、若手表显示是9点30分.①求此时时针与分针的夹角的大小;
②此时,作射线 , 使 , 求的大小;
(3)、自9点30分起,至10点30分止,在这一小时期间,时针和分针在不停地旋转.若射线是的平分线,它也随之运动,则经过多少分钟后,恰好能使?23. 如图,已知 , 在内部,在的内部,. (1)、若 , 则;若 , 则(用含的代数式表示);(2)、若 , 求的度数;(3)、将以OC为折痕进行翻折,落在处,将以为折痕进行翻折,落在处,的度数变化时,的度数是否发生变化?若变化,请说明理由:若不变,请求出的度数.24. 含有的直角三角板和含有的直角三角板按如图1放置,和重合.
(1)、若 , 则;若 , 则(用含的代数式表示);(2)、若 , 求的度数;(3)、将以OC为折痕进行翻折,落在处,将以为折痕进行翻折,落在处,的度数变化时,的度数是否发生变化?若变化,请说明理由:若不变,请求出的度数.24. 含有的直角三角板和含有的直角三角板按如图1放置,和重合.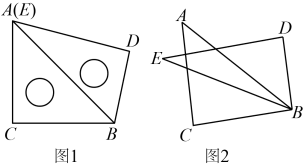
【操作一】三角板保持不变,将三角板绕着点以每秒的速度按逆时针方向旋转.当它完成旋转一周时停止,设旋转的时间为t秒.
(1)、当时,度.(2)、求t为何值时,.【操作二】如图2,在三角板绕着点B以每秒的速度按逆时针方向旋转的同时,三角板也绕着点B以每秒的速度按逆时针方向旋转,设旋转时间为t秒().
(3)、求t为何值时,与重合.(4)、试探索:在两个三角板旋转的过程中,是否存在某个时刻,使得与中其中一个角是另一个角的两倍?若存在,请求出所有满足题意的t的值;若不存在,请说明理由.