【北师大版】2023-2024学年数学八年级(上)期末仿真模拟试题(二)
试卷更新日期:2023-12-13 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 在平面直角坐标系中,第四象限内有一点 , 它到轴的距离为( )A、3 B、-3 C、4 D、-42. 已知△ABC的三个内角分别为∠A、∠B、∠C,三边分别为a、b、c,下列条件不能判定△ABC是直角三角形的是( )A、∠A:∠B:∠C=3:4:7 B、∠A=∠B-∠C C、a:b:c=2:3:4 D、b2=(a+c) (a-c)3. 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
甲
乙
丙
丁
平均数(环)
9.1
9.1
9.1
9.1
方差
7.6
8.6
9.6
9.7
根据表中数据,要从中选择一名成绩发挥稳定的运动员参加比赛,应选择( )
A、甲 B、乙 C、丙 D、丁4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,将一块三角尺的直角顶点放在直线a上,a∥b , 则∠2=( ) A、80° B、70° C、60° D、50°6. 如图为正比例函数y=kx(k≠0)的图象,则一次函数y=x+k的大致图象是( )
A、80° B、70° C、60° D、50°6. 如图为正比例函数y=kx(k≠0)的图象,则一次函数y=x+k的大致图象是( )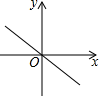 A、
A、 B、
B、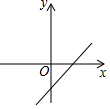 C、
C、 D、
D、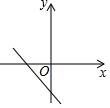 7. 下列说法中,正确的是( )A、在角的内部到角的两边距离相等的点一定在这个角的平分线上 B、一个三角形两边的垂直平分线的交点到这个三角形三边的距离相等 C、“若a>b,则a2>b2”的逆命题是真命题 D、用反证法证明“三角形中必有一个角不大于60°”,先假设这个三角形中有一个内角大于60°8. 为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:每月用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费. 如图是张磊家2021年9月和10月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度( )
7. 下列说法中,正确的是( )A、在角的内部到角的两边距离相等的点一定在这个角的平分线上 B、一个三角形两边的垂直平分线的交点到这个三角形三边的距离相等 C、“若a>b,则a2>b2”的逆命题是真命题 D、用反证法证明“三角形中必有一个角不大于60°”,先假设这个三角形中有一个内角大于60°8. 为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:每月用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费. 如图是张磊家2021年9月和10月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度( )代收电费收据
2021年9月
电表号
1205
户名
张磊
月份
9月
用电量
220度
金额
112元
代收电费收据
2021年10月
电表号
1205
户名
张磊
月份
10月
用电量
265度
金额
139元
A、0.5元,0.6元 B、0.4元,0.5元 C、0.3元,0.4元 D、0.6元,0.7元9. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( ) A、 B、 C、6 D、10. 小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A、 B、 C、6 D、10. 小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )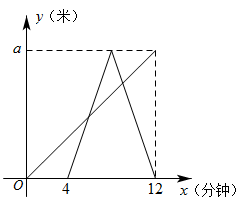 A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟
A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟二、填空题(每题3分,共15分)
-
11. 计算: .12. 点A (-4,3)关于x轴的对称点的坐标是13. 某射击运动员射击10次的成绩统计如下:
成绩(环)
5
6
7
8
9
10
次数(次)
3
2
2
1
1
1
则该射击运动员的平均成绩为环.
14. 如图,直线与直线交于点E(3,1),则关于x,y的二元一次方程组的解为 .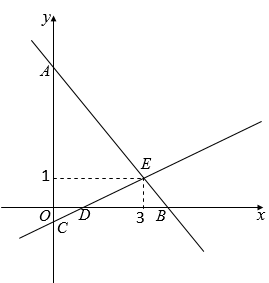 15. 如图,小方格都是边长为1的正方形,则中边上的高是 .
15. 如图,小方格都是边长为1的正方形,则中边上的高是 .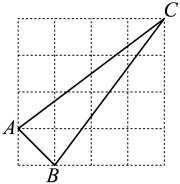
三、解答题(共7题,共55分)
-
16. 计算:(1)、 ;(2)、 .17. 请用指定的方法解下列方程组:(1)、;(代入消元法)(2)、 . (加减消元法)18. 八年级二班举办了主题为“致敬航天人,共筑星河梦”的演讲比赛.由学生1,学生2,老师、班长一起组成四人评委团,对演讲者现场打分,满分10分.图1是甲、乙二人的演讲得分的不完整折线图,已知二人得分的平均数都是8分.
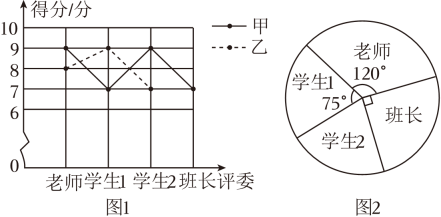 (1)、班长给乙的打分是 ▲ 分,补全折线图;(2)、在参加演讲的同学中,如果某同学得分的四个数据的方差越小,则认为评委对该同学演讲的评价越一致.请通过计算推断评委对甲、乙两位同学中哪位同学的评价更一致;(3)、要在甲、乙两位同学中选出一人参加年级的演讲比赛.按照扇形统计图(图2)中各评委的评分占比,分别计算两人各自的最后得分,得分高的能被选中,请判断谁被选中.19. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。
(1)、班长给乙的打分是 ▲ 分,补全折线图;(2)、在参加演讲的同学中,如果某同学得分的四个数据的方差越小,则认为评委对该同学演讲的评价越一致.请通过计算推断评委对甲、乙两位同学中哪位同学的评价更一致;(3)、要在甲、乙两位同学中选出一人参加年级的演讲比赛.按照扇形统计图(图2)中各评委的评分占比,分别计算两人各自的最后得分,得分高的能被选中,请判断谁被选中.19. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。 (1)、求证:△ACE≌△BCD:(2)、若CB= , AD=2,求DE的长.20. 希望中学为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红和小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元,且买甲种笔记本30个比买乙种笔记本20个少花10元.(1)、求甲、乙两种笔记本的单价各是多少元?(2)、为了奖励更多的同学,学校决定再次购进甲、乙两种笔记本,若买甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购买这两种笔记本的总金额不超过320元,求这次购买乙种笔记本最多多少个?21. 小明在学习一次函数后,对形如(其中k,m,n为常数,且)的一次函数图象和性质进行了探究,过程如下:
(1)、求证:△ACE≌△BCD:(2)、若CB= , AD=2,求DE的长.20. 希望中学为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红和小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元,且买甲种笔记本30个比买乙种笔记本20个少花10元.(1)、求甲、乙两种笔记本的单价各是多少元?(2)、为了奖励更多的同学,学校决定再次购进甲、乙两种笔记本,若买甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购买这两种笔记本的总金额不超过320元,求这次购买乙种笔记本最多多少个?21. 小明在学习一次函数后,对形如(其中k,m,n为常数,且)的一次函数图象和性质进行了探究,过程如下: (1)、【特例探究】
(1)、【特例探究】如图所示,小明分别画出了函数 , , 的图象.请你根据列表、描点、连线的步骤在图中画出函数的图象.
(2)、【深入探究】通过对上述几个函数图象的观察、思考,你发现(k为常数,且)的图象一定会经过的点的坐标是 .
(3)、【得到性质】函数(其中k、m、n为常数,且)的图象一定会经过的点的坐标是 .
(4)、【实践运用】已知一次函数(k为常数,且)的图象一定过点N,且与y轴相交于点A,若的面积为4,则k的值为 .
22. 如图,已知直线l1:y=2x﹣3与直线l2:y=﹣x+3相交于点P,分别与y轴相交于点A、B.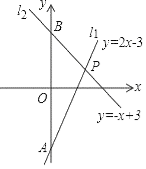 (1)、求点P的坐标;(2)、点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.
(1)、求点P的坐标;(2)、点M(0,k)为y轴上的一个动点,过点M作y轴的垂线交l1和l2于点N,Q,当NQ=2时,求k的值.