【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略1 三角形的基础知识

试卷更新日期：2023-12-13 类型：复习试卷

进入出卷网下载

一、选择题

1. 以下列各组线段为边，能构成三角形的是（）

A、2，6，3 B、6，7，8 C、1，7，9 D、 $\frac{3}{2} ， 4 ， \frac{5}{2}$

查看试题解析
2. 以下列长度（单位：cm）的三条线段为边，能组成三角形的是（）

A、3，4，8 B、4，5，9 C、4，4，4 D、1，2，3

查看试题解析
3. 在△ABC中作AB边上的高，下列画法正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图， $△ A B C$ 中AD为中线， $A B = 8 ， A C = 6$ ，则 $△ A B D$ 与 $△ A C D$ 的周长之差为（）

A、1 B、2 C、3 D、4

查看试题解析
5. $△ A B C$ 三个内角的度数之比为3：4：5，那么 $△ A B C$ 是（）

A、等腰三角形 B、锐角三角形 C、钝角三角形 D、直角三角形

查看试题解析
6. 如图， $△ A B C ≌ △ A D E$ ， $∠ B = 30 °$ ， $∠ E = 20 °$ ， $∠ B A E = 90 °$ ，则 $∠ E A C =$ （）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
7. 根据下列已知条件，能画出唯一的△ABC的是（）

A、∠C=90°，AB=6 B、∠A=60°，∠B=45°，AB=4 C、AB=4，BC=3，∠A=30° D、AB=3，BC=4，CA=8

查看试题解析
8. 如图， $A O$ ， $B O$ 分别平分 $∠ C A B$ ， $∠ C B A$ ，且点 $O$ 到 $A B$ 的距离 $O D = 2 c m$ ， $△ A B C$ 的周长为 $14 c m$ ，则 $△ A B C$ 的面积为（）

A、 $7 c m^{2}$ B、 $14 c m^{2}$ C、 $21 c m^{2}$ D、 $28 c m^{2}$

查看试题解析
9. 如图，从 $△ A B C$ 各顶点作平行线 $A D ∥ E B ∥ F C$ ，各与其对边或其延长线相交于点D，E，F.若 $△ A B E$ 的面积为 $S_{1}$ ， $△ A F C$ 的面积为 $S_{2}$ ， $△ E D C$ 的面积为 $S_{3}$ ，只要知道下列哪个值就可以求出 $△ D E F$ 的面积（）

A、 $S_{1} + S_{2}$ B、 $S_{1} + S_{2} + S_{3}$ C、 $S_{3}$ D、 $S_{1} + S_{2} + 2 S_{3}$

查看试题解析
10. 如图，以直角三角形 $A B C$ 的各边边长分别向外做等边三角形，再把较小的两个三角形按如图2的方式放置在最大的三角形内， $S_{1}$ 是小梯形面积， $S_{2}$ 是三个三角形重叠部分的面积， $S_{3}$ 是大梯形的面积， $S_{4}$ 是平行四边形的面积，则下列关系一定成立的是（）

A、 $S_{1} = S_{4}$ B、 $S_{2} = S_{4}$ C、 $S_{3} = S_{4}$ D、 $S_{1} = S_{3}$

查看试题解析

二、填空题

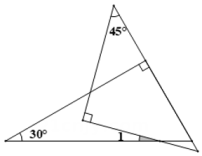
11. 在△ABC中，∠A=45°，∠B=75°，则∠C的度数为.

查看试题解析
12. 已知等腰三角形的一边长为3，另一边长为6，则它的周长为.

查看试题解析
13. 若等腰三角形的一个内角为 $85 °$ ，则底角为.

查看试题解析
14. 如图，将一副三角板如图方式放置，则∠1的度数是°．

查看试题解析
15. 如图，在 $△ A B C$ 中，点D、E、F分别是线段BC、AD、CE的中点，且 $S_{△ A B C} = 16 c m^{2}$ ，则 $S_{△ B E F} =$ $c m^{2}$ .

查看试题解析
16. 若三角形的周长为13，且三边均为整数，则满足条件的三角形有种．

查看试题解析

三、解答题

17. 已知 $△ A B C$ (如图).

（1）用尺规作出AC边上的中线；
（2）用三角尺画BC比上的高线.

查看试题解析
18. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高线， $C E$ 是一条角平分线，它们相交于点P.已知 $∠ A P E = 55 °$ ， $∠ A E P = 80 °$ ，求 $∠ B A C$ 的度数.

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ A C B =90 °$ ， $∠ B =50 °$ ， CD是 $△ A B C$ 的高线，CE是 $△ A B C$ 的角平分线，求 $∠ D C E$ 的度数．

查看试题解析
20. 如图，在△ABC中，AD是BC边上的高线，AE平分∠BAC，若∠BAC：∠B：∠C＝4：3：2，求∠DAE的度数．

查看试题解析
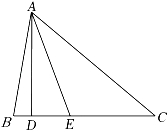21. 如图，在△ABC中，点D，E分别在AB，BC上，且 $D E / / A C ， ∠ 1 = ∠ 2$ .

(1)、求证： $A F / / B C$ ；

(2)、若AC平分 $∠ B A F ， ∠ B = 4 8^{°}$ ，求 $∠ 1$ 的度数.

查看试题解析
22. 如图①，△ABC的角平分线BD、CE相交于点P．

(1)、如果∠A＝80°，求∠BPC的度数；

(2)、如图②，过P点作直线MN，分别交AB和AC于点M和N，且MN平行于BC，则有∠MPB+∠NPC＝90° $- \frac{1}{2}$ ∠A．若将直线MN绕点P旋转，
（ⅰ）如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立，并说明理由；

（ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（ⅰ）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由．

查看试题解析
23. 如果三角形的两个内角α与β满足2α+β＝90°，那么我们称这样的三角形为“准直角三角形”．

(1)、如图①，在Rt△ABC中，∠ACB＝90°，BD是△ABC的角平分线．
求证：△ABD是“准直角三角形”．

(2)、关于“准直角三角形”，下列说法：
①在△ABC中，若∠A＝100°，∠B＝70°，∠C＝10°，则△ABC是准直角三角形；

②若△ABC是“准直角三角形”，∠C＞90°，∠A＝60°，则∠B＝20°；

③“准直角三角形”一定是钝角三角形．其中，正确的是．（填写序号）

(3)、如图②，B、C为直线l上两点，点A在直线l外，且∠ABC＝50°．若P是l上一点，且△ABP是“准直角三角形”，请直接写出∠APB的度数．

查看试题解析