浙教版数学七年级上册期末冲刺满分攻略15 线段、射线和直线

试卷更新日期：2023-12-13 类型：复习试卷

进入出卷网下载

一、选择题

1. 经过刨平的木板上的两点，能弹出一条笔直的墨线，且只能弹出一条这样的墨线，理由是（）

A、两点确定一条直线 B、两点之间线段最短 C、连结直线外一点与直线上各点的所有线段中，垂线段最短 D、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线

查看试题解析
2. 下列四个说法：①两点确定一条直线；②过直线上一点有且只有一条直线垂直于已知直线；③连接直线外一点与直线上各点的所有线段中，垂线段最短；④从直线外一点到这条直线的垂线段，叫做点到直线的距离，其中正确的说法的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 如图，在三角形ABC中，线段AB+AC>BC，其理由是（）

A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、同一平面内，过一点有且只有一条直线垂直于已知直线

查看试题解析
4. 下列四个图中，能表示线段 $x = \frac{1}{2} (a + c - b)$ 的是（）

A、 B、 C、 D、

查看试题解析
5. 小王准备从A地去往B地，打开导航，显示两地距离为50km，但导航提供的三条可选路线长却分别为56km，66km，61km（如图）．能解释这一现象的数学知识是（）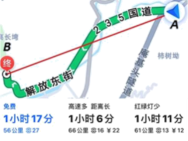

A、两点之间，线段最短 B、垂线段最短 C、两点之间，直线最短 D、两点确定一条直线

查看试题解析
6. 如图，已知线段 $a$ ， $b$ ，画一条射线 $O M$ ，在射线 $O M$ 上依次截取 $O A = A B = a$ ，在线段 $B O$ 上截取 $B C = b$ .则（）

A、 $O B = a + b$ B、 $O B = 2 b - a$ C、 $O C = b - a$ D、 $O C = 2 a - b$

查看试题解析
7. 已知线段AB，在线段AB的延长线上取一点C，使 $B C = 2 A B$ ．若 $A C = 9 cm$ ，则线段AB的长度为（）

A、4.5cm B、4cm C、3cm D、2cm

查看试题解析
8. 下列说法中，正确的是（）

A、两点之间直线最短 B、如果∠α＝53°38'，那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在，那么这个角的余角比这个角的补角小 D、相等的角是对顶角

查看试题解析
9. 棋盘上有黑、白两色棋子若干，如果两颗棋子连成的直线上只有颜色相同的棋子，我们就称“同棋共线”．右图中“同棋共线”的直线共有（）

A、8条 B、10条 C、12条 D、16条

查看试题解析
10. 在下列生活、生产现象中，不可以用基本事实“两点确定一条直线”来解释的有（）

A、用两颗钉子就可以把木条固定在墙上； B、当木工师傅锯木板时，他会用墨盒在木板上弹出墨线，这样会使木板沿直线锯下； C、把弯曲的公路改直，就能缩短路程； D、在正常情况下，射击时只要保证瞄准的一只眼在两个准星确定的直线上，就能射中目标．

查看试题解析

二、填空题

11. 如图，以点О为端点的射线有条.

查看试题解析
12. 已知A，B是数轴上的两点，点A表示的数是-1，且线段AB的长度为6，则点B表示的数是.

查看试题解析
13. 将线段AB延长至点C，使BC= $\frac{1}{2}$ AB，D为线段AC的中点，若BD=2，则线段AB的长为．

查看试题解析
14. 如图，点C，M，N在线段AB上， $A C = 12 ， B C = 6 ， A M = \frac{1}{3} A C ， B N = \frac{1}{3} B C$ .则线段MN的长为.

查看试题解析
15. 如图1，一款暗插销由外壳 $A B$ ，开关 $C D$ ，锁芯DE三部分组成，其工作原理如图2，开关 $C D$ 绕固定点O转动，由连接点D带动锁芯DE移动.图3为插销开启状态，此时连接点D在线段 $A B$ 上，如 $D_{1}$ 位置.开关 $C D$ 绕点O顺时针旋转180°后得到 $C_{2} D_{2}$ ，锁芯弹回至 $D_{2} E_{2}$ 位置（点B与点 $E_{2}$ 重合），此时插销闭合如图4.已知 $C D = 74 m m$ ， $A D_{2} - A C_{1} = 50 m m$ ，则 $B E_{1} =$ mm.

查看试题解析
16. 有一无弹性细线，拉直时测得细线 $O P$ 长为 $8 cm$ ，现进行如下操作：1.在细线上任取一点 $A$ ；2.将细线折叠，使点 $O$ 与点 $A$ 重合，记折点为点 $B$ ；3.将细线折叠，使点 $P$ 与点 $A$ 重合，记折点为点 $C$ .

(1)、如图， $B C$ 的长为 $cm$ ；

(2)、继续进行折叠，使点 $B$ 与点 $C$ 重合，并把 $B$ 点和与其重叠的 $C$ 点处的细线剪开，使细线分成长为 $a$ ， $b$ ， $c$ 的三段 $(a < b < c)$ ，当 $a ： b = 1 ： 3$ ，则细线未剪开时 $O A$ 的长为 $cm$ .

查看试题解析

三、解答题

17. 小明和小亮在讨论“射击时为什么枪管上要有准星？”
小明：过两点有且只有一条直线，所以枪管上要有准星．
小亮：若将人眼看成一点，准星看成一点，目标看成一点，这不就有三点了吗？多了一个点呀！
请你说说你的观点．

查看试题解析
18. 如图，已知直线l表示一段公路，点A表示学校，点B表示书店，点C表示图书馆.

⑴请画出学校A到书店B的最短路线.
⑵在公路l上找一个路口M，使得 $A M + C M$ 的值最小.
⑶现要从学校A向公路l修一条小路，怎样修路才能使小路的长最短？请画出小路的路线，并用所学知识描述小路的方向.

查看试题解析
19. 如图，C为线段 $A D$ 上一点，点B为 $C D$ 的中点，且 $A D = 9 c m ， B D = 2 c m$ .

(1)、图中共有条线段.

(2)、求 $A C$ 的长.

(3)、若点E在直线 $A D$ 上，且 $E A = 3 c m$ ，求BE的长.

查看试题解析
20. 如图，点 $C$ 是直线 $A B$ 上一点，点 $M$ 是线段 $A C$ 的中点.

(1)、若 $A B = 8$ ，点 $C$ 在线段 $A B$ 上，且 $A C = 3 B C$ ，则 $A M$ 的长为.

(2)、若 $A B = a$ ， $A B - A C = \frac{a}{3}$ ，求 $B M$ 的长（用含 $a$ 的代数式表示）.

查看试题解析
21.
已知数轴的原点为O，如图所示，点A表示﹣2，点B表示3，请回答下列问题：
（1）数轴是什么图形？数轴在原点右边的部分（包括原点）是什么图形？数轴上表示不小于﹣2，且不大于3的部分是什么图形？请你分别给它们取一个合适的名字；
（2）请你在射线AO上再标上一个点C（不与A点重合），那么表示点C的值x的取值范围是

查看试题解析
22. 某操作车间有一段直线型向左移动的传输带， $A$ ， $B$ 两位操作工人站于传输带同侧且相距16米，操作组长 $F$ 也站在该侧，且到 $A$ ， $B$ 距离相等，传输带上有一个8米长的工具筐 $C E$ ．

(1)、如图1，当 $C E$ 位于 $A$ ， $B$ 之间时， $F$ 发现工具筐的 $C$ 端离自己只有 1米，则工具筐 $C$ 端离 $A$ 米，工具筐 $E$ 端离 $B$ 米．

(2)、工具筐 $C$ 端从 $B$ 点开始随传输带向左移动直至工具筐 $E$ 端到达以A点为止，这期间工具筐 $E$ 端到 $B$ 的距离 $B E$ 和工具筐 $E$ 端到 $F$ 的距离 $E F$ 存在怎样的数量关系，并用等式表示，（你可以在图2中先画一画，再找找规律）

查看试题解析
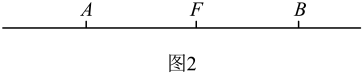23. 如图，线段 $A B$ 的中点O是数轴原点，点C在点O右侧，分线段 $A B$ 的长度为 $3 ： 2$ ，且 $O C = 3$ .

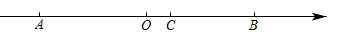(1)、求点A在数轴上代表的数是什么？请说明理由.

(2)、若点P从点C出发，以3个单位/秒的速度向点A运动，到点A停止；点Q从点O出发，以1个单位/秒速度向点B运动，到点B后停止.问运动时间t为几秒时， $P A = Q B$ ？

查看试题解析
24. 问题提出：
如图1，A、B、C、D表示四个村庄，村民们准备合打一口水井.

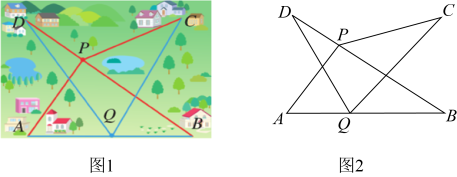(1)、问题解决：
若水井的位置现有P、Q两种选择方案.点P在线段 $B D$ 上，点Q在线段 $A B$ 上，哪一种方案的水井到各村庄的距离总和较小？请说明你判断的理由.

(2)、你能给出一种使水井到各村庄的距离之和最小的方案吗？若能，请图2中标出水井的位置点M，并说明理由.

(3)、问题拓展：
如果（2）问中找出的水井经过招标，由两个工程队修建（不存在同时修建）. 已知甲工程队单独完成需要80天，乙工程队单独完成需要120天，且甲工程队比乙工程队每天多修建 $0.5 m$ .
问水井要修建几米？

(4)、若甲工程队每天的施工费为0.5万元，乙工程队每天的费用是0.25万元，为了缩短工期和节约资金，则甲工程队最多施工几天才能使工程款不超过35万元？（甲、乙两队的施工时间不足一天按一天算）.

查看试题解析