【北师大版】2023-2024学年数学九年级(上)期末仿真模拟试题(三)
试卷更新日期:2023-12-13 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 如图,下面几何体是由一个圆柱被经过上下底面圆心的平面截得的,则它的左视图是( )
 A、
A、 B、
B、 C、
C、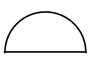 D、
D、 2. 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为BC边上一动点,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为( )
2. 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为BC边上一动点,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为( )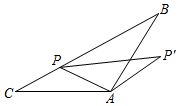 A、 B、 C、 D、3. 方程2x2+x-4=0的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根4. 在Rt△ABC中,∠C=90°,若sinA= ,AB=2,则AC长是( )A、
A、 B、 C、 D、3. 方程2x2+x-4=0的解的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根4. 在Rt△ABC中,∠C=90°,若sinA= ,AB=2,则AC长是( )A、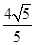 B、
C、
D、2
5. 生活中到处可见黄金分割的美.如图,点将线段分成、两部分,且 , 如果 , 那么称点为线段的黄金分割点.若是线段的黄金分割点, , 则分割后较短线段长为( )
B、
C、
D、2
5. 生活中到处可见黄金分割的美.如图,点将线段分成、两部分,且 , 如果 , 那么称点为线段的黄金分割点.若是线段的黄金分割点, , 则分割后较短线段长为( ) A、 B、 C、 D、6. 一个不透明的口袋中装着只有颜色不同的红、白两球共10个,搅匀后从中随机摸出一个球,记下它的颜色后放回搅匀,如此这样共摸球100次,发现70次摸到红球,估计这个口袋中有( )个红球.A、7 B、8 C、9 D、107. 如图,在直角坐标系中,点A在第一象限内,点B在x轴正半轴上,以点O为位似中心,在第三象限内与ΔOAB的位似比为 的位似图形ΔOCD.若点C的坐标为 ,则点A的坐标为( )
A、 B、 C、 D、6. 一个不透明的口袋中装着只有颜色不同的红、白两球共10个,搅匀后从中随机摸出一个球,记下它的颜色后放回搅匀,如此这样共摸球100次,发现70次摸到红球,估计这个口袋中有( )个红球.A、7 B、8 C、9 D、107. 如图,在直角坐标系中,点A在第一象限内,点B在x轴正半轴上,以点O为位似中心,在第三象限内与ΔOAB的位似比为 的位似图形ΔOCD.若点C的坐标为 ,则点A的坐标为( ) A、 B、 C、 D、8. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O , 点E为BC边上的一个动点,EF⊥AC , EG⊥BD , 垂足分别为点F , G , 则EF+EG的值为( )
A、 B、 C、 D、8. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O , 点E为BC边上的一个动点,EF⊥AC , EG⊥BD , 垂足分别为点F , G , 则EF+EG的值为( ) A、 B、 C、 D、9. 如图,在正方形 中,点E在对角线 上,连接 , 于点E,交 于点F,连接 ,已知 , ,则 的面积为( )
A、 B、 C、 D、9. 如图,在正方形 中,点E在对角线 上,连接 , 于点E,交 于点F,连接 ,已知 , ,则 的面积为( ) A、4 B、5 C、10 D、10. 一花户,有26m长的篱笆,要围成一边靠住房墙(墙长12m)的面积为的长方形花园,且垂直于住房墙的一边留一个1m的门,设垂直于住房墙的其中一边长为x,则可列方程为( )
A、4 B、5 C、10 D、10. 一花户,有26m长的篱笆,要围成一边靠住房墙(墙长12m)的面积为的长方形花园,且垂直于住房墙的一边留一个1m的门,设垂直于住房墙的其中一边长为x,则可列方程为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 若 , 则的值等于 .12. 计算.13. 若m,n是一元二次方程的两个实数根,则 .14. 如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,4)也在此函数的图象上,则a= .
 15. 如图,正方形中,A,C分别在x,y正半轴上,反比例函数的图象与边分别交于点D,E,且 , 对角线把分成面积相等的两部分,则 .
15. 如图,正方形中,A,C分别在x,y正半轴上,反比例函数的图象与边分别交于点D,E,且 , 对角线把分成面积相等的两部分,则 .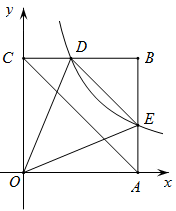
三、解答题
-
16. 解方程: .17. 将A、B、C、D四人随机分成甲乙两组参加乒乓球双打比赛,求A、B同时分在甲组的概率.18. 如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度.已知标杆BE的高为1m,测得AB=2m,AC=10m,求建筑物CD的高.
 19. 如图,四边形为菱形,点E在AC的延长线上, .
19. 如图,四边形为菱形,点E在AC的延长线上, .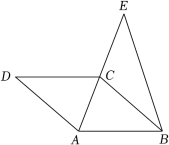 (1)、求证:;(2)、当 , 时,求AE的长.20. 如图1,在△ABC中,∠A=90°,AB=6,AC=8,点D , F分别是边AB , BC上的动点,点D不与点A , B重合,过点D作DE BC , 交AC于点E , 连接DF , EF .
(1)、求证:;(2)、当 , 时,求AE的长.20. 如图1,在△ABC中,∠A=90°,AB=6,AC=8,点D , F分别是边AB , BC上的动点,点D不与点A , B重合,过点D作DE BC , 交AC于点E , 连接DF , EF . (1)、当DF⊥BC时,求证:△FBD∽△ABC;(2)、在(1)的条件下,当四边形BDEF是平行四边形时,求BF的长;(3)、是否存在点F , 使得△FDE为等腰直角三角形?若不存在,请说明理由;若存在,请求出DE的长.21. 如图,在中, , D、E分别是的中点,连接 . 点P从点D出发,沿方向匀速运动,速度为;同时,点Q从点B出发,沿方向匀速运动,速度为 , 当点P停止运动时,点Q也停止运动.连接 , 设运动时间为 . 解答下列问题:
(1)、当DF⊥BC时,求证:△FBD∽△ABC;(2)、在(1)的条件下,当四边形BDEF是平行四边形时,求BF的长;(3)、是否存在点F , 使得△FDE为等腰直角三角形?若不存在,请说明理由;若存在,请求出DE的长.21. 如图,在中, , D、E分别是的中点,连接 . 点P从点D出发,沿方向匀速运动,速度为;同时,点Q从点B出发,沿方向匀速运动,速度为 , 当点P停止运动时,点Q也停止运动.连接 , 设运动时间为 . 解答下列问题: (1)、cm,(用含有t的代数式表示)(2)、请求出t为何值时,以点E、P、Q为顶点的三角形与相似?(3)、当t为何值时,为等腰三角形?(直接写出答案即可).22. 【综合与实践】:阅读材料,并解决以下问题.
(1)、cm,(用含有t的代数式表示)(2)、请求出t为何值时,以点E、P、Q为顶点的三角形与相似?(3)、当t为何值时,为等腰三角形?(直接写出答案即可).22. 【综合与实践】:阅读材料,并解决以下问题.【学习研究】:北师大版教材九年级上册第39页介绍了我国数学家赵爽在其所著的《勾股圆方图注》中关于一元二次方程的几何解法:以为例,构造方法如下:
首先将方程变形为 , 然后画四个长为 , 宽为的矩形,按如图(1)所示的方式拼成一个“空心”大正方形,则图中大正方形的面积可表示为 , 还可表示为四个矩形与一个边长为2的小正方形面积之和,即 , 因此,可得新方程: , 表示边长, , 即 , 遗憾的是,这样的做法只能得到方程的其中一个正根.

【类比迁移】:小明根据赵爽的办法解方程 , 请你帮忙画出相应的图形,将其解答过程补充完整:
第一步:将原方程变形为 , 即( ▲ )=4;
第二步:利用四个面积可用表示为 ▲ 的全等矩形构造“空心”大正方形(请在画图区画出示意图,标明各边长),并写出完整的解答过程;
第三步:
【拓展应用】:一般地对于形如:一元二次方程可以构造图2来解,已知图2是由4个面积为3的相同矩形构成,中间围成的正方形面积为4.那么此方程的系数 ▲ , ▲ , 求得方程的一个正根为 ▲ .