2023-2024学年浙教版数学九年级（上）期末仿真模拟卷（杭州适用，九上全册）

试卷更新日期：2023-12-13 类型：期末考试

进入出卷网下载

一、选择题

1. 下列函数解析式中，一定为二次函数的是（）

A、 $s = 2 t^{2} - 2 t + 1$ B、 $y = a x^{2} + b x + c$ C、 $y = 3 x - 1$ D、 $y = x^{2} + \frac{1}{x}$

查看试题解析
2. 二次函数 $y = - 5 {(x + 2)}^{2} - 6$ 的开口方向、对称轴和顶点坐标分别为（）

A、向下、直线 $x = 2$ 、 $(2 ， 6)$ B、向下、直线 $x = - 2$ 、 $(- 2 ， - 6)$ C、向下、直线 $x = - 2$ 、 $(- 2 ， 6)$ D、向上、直线 $x = 2$ 、 $(2 ， - 6)$

查看试题解析
3. 如图所示，这是一幅长方形宣传画，长为4 m，宽为2 m.为测量画上图案的面积，现将宣传画平铺在地上，向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的)，经过大量重复投掷试验，发现骰子落在图案中的频率稳定在常数0.4左右.由此可估计宣传画上图案的面积为（）

A、2.4 m² B、3.2 m² C、4.8 m² D、7.2 m²

查看试题解析
4. 已知 $⊙ O$ 的半径为 $2$ ， $O A = \sqrt{5}$ ，则点 $A$ 和 $⊙ O$ 的位置关系是（）

A、点 $A$ 在圆上 B、点 $A$ 在圆外 C、点 $A$ 在圆内 D、不确定

查看试题解析
5. 下列事件中，必然事件的是（）

A、明天太阳从西边升起 B、a是实数，则 $| a | \geq 0$ C、某运动员跳高的最好成绩是20.1米 D、班级里有两位同学同年同月同日生

查看试题解析
6. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE=1寸，AB=10寸，则直径CD的长度是（　　）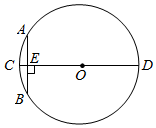

A、12寸 B、24寸 C、13寸 D、26寸

查看试题解析
7. 如图，四边形ABCD是圆内接四边形，∠BAD=108°，E是BC延长线上一点，若∠ECF=60°，则∠DCF的大小是（　　）

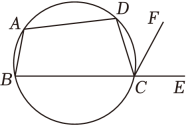A、30° B、48° C、54° D、60°

查看试题解析
8. 已知 $\frac{a}{4} = \frac{b}{3}$ ，则 $\frac{a - b}{b}$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、3 D、 $\frac{1}{3}$

查看试题解析
9. 两相似三角形的相似比为2：3，它们的面积之差为15，则这两个三角形的面积之和是（）

A、39 B、75 C、76 D、40

查看试题解析
10. 《九章算术》的“勾股”章中有这样一个问题：“今有邑方不知大小，各中开门.出北门二十步有木.出南门十四步，折而西行一千七百七十五步见木.问邑方几何.”大意是：如图所示，四边形 $E F G H$ 是一座正方形小城，北门 $A$ 位于 $F G$ 的中点，南门 $B$ 位于 $E H$ 的中点.从北门出去正北方向20步远的 $C$ 处有一树木.从南门出去向南行走14步，再向西行走1775步，恰好能看见 $C$ 处的树木.正方形小城的边长为（）

A、105步 B、200步 C、250步 D、305步

查看试题解析

二、填空题

11. 飞机着陆后滑行的距离y（单位： m）关于滑行时间t：（单位： s）的函数解析式是 $y = 60 t - \frac{6}{5} t^{2}$ ，从飞机着陆至停下来共滑行米.

查看试题解析
12. 王芳抛一枚硬币10次，有8次正面朝上，当她抛第11次，正面朝上的概率．

查看试题解析
13. 如图，在△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转，得到△EDC，使点B的对应点D恰好落在AB边上，AC、ED交于点F．若∠BCD=50°，则∠EFC=度．

查看试题解析
14. 如图，AB，CD是⊙O的直径．若∠AOC=70°，则 $\overset{⌢}{A C}$ 的度数是， $\overset{⌢}{B D}$ 的度数是， $\overset{⌢}{A D}$ 的度数是.

查看试题解析
15. 如图，直线GH与正六边形ABCDEF的边AB、EF分别交于点G、H，若∠FHG= 70°，则∠AGH=度．

查看试题解析
16. 如图，在抛物线y＝x²的内部依次画正方形，使对角线在y轴上，另两个顶点落在抛物线上．按此规律类推，第2023个正方形的边长是．

查看试题解析

三、解答题

17. 求二次函数y=-2x²+8x-5的最大值(或最小值)和对应自变量的值．

查看试题解析
18. 如图，在直角坐标中，矩形 $O A B C$ 的顶点O与坐标原点重合，顶点A、C分别在x轴和y轴上，点B的坐标为 $(2 ， 3)$ ，反比例函数 $y = \frac{k}{x}$ 是的图象经过 $B C$ 的中点D，且与 $A B$ 交于点E，连接 $D E$ ．

(1)、求k的值及点E的坐标；

(2)、若点F是 $O C$ 边上一点，且 $△ F B C ∽ △ D E B$ ，求直线 $F B$ 的解析式．

(3)、若点P在y轴上，且 $△ O P D$ 的面积与四边形 $B D O E$ 的面积相等，求点P的坐标．

查看试题解析
19. 如图，有一座拱桥是圆弧形，它的跨度AB＝60米，拱高PD＝18米.

(1)、求圆弧所在的圆的半径r的长；

(2)、当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE＝4米时，是否要采取紧急措施？

查看试题解析
20. 一个布袋里装有只有颜色不同的3个球，其中2个红球，1个白球.

(1)、从中任意摸出一个球，求摸出的是红球的概率.

(2)、从中任意摸出一个球，记下颜色后放回，搅匀，再摸出一个球，请画出树状图或列表，并求摸出的2个球中，1个是白球，1个是红球的概率.

查看试题解析
21.
在平面直角坐标系中，抛物线y＝ax²+bx+c（a≠0）经过点A（-1，0）和B（0，3），其顶点的横坐标为1．

(1)、求抛物线的表达式．

(2)、若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．

(3)、若点P为抛物线y＝ax²+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．

查看试题解析
22. 如图， $⊙ O$ 的半径为1，直径 $A B$ ， $C D$ 的夹角 $∠ A O D = 60 °$ ，点 $P$ 是 $\overset{⌢}{B D}$ 上一点，连接 $P A$ ， $P C$ 分别交 $C D$ ， $A B$ 于点 $M$ ， $N$ .

(1)、若 $P C ⊥ A B$ ，求证： $P A ⊥ C D$ ；

(2)、当点 $P$ 在 $\overset{⌢}{B D}$ 上运动时.
①猜想：线段 $A M$ 与 $C N$ 有怎样的数量关系，并给出证明；
②求证： $P A + P C = \frac{3}{A M}$ .

查看试题解析
23. 已知， $A B$ 是 $⊙ O$ 直径，弦 $C D ⊥ A B$ 于点 $H$ ，点 $P$ 是 $⊙ O$ 上一点．

(1)、如图1，连接 $P B$ 、 $P C$ 、 $P D$ ，求证： $B P$ 平分 $∠ C P D$ ；

(2)、如图2，连接 $P A$ 、 $P C$ 、 $P D$ ， $P C$ 交 $A B$ 于点 $E$ ，交 $A D$ 于点 $F$ ，若 $A E = A P$ ；求证： $C E = D P$ ；

(3)、如图 $3$ ，在（2）的条件下，连接 $B P$ 交 $A D$ 于 $G$ ，连接 $O G$ ，若 $∠ O G A = 45 °$ ， $S_{△ A O G} = 30$ ，求 $⊙ O$ 半径．

查看试题解析