天津市河东区2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、选择题(本大题共12小题,共36分)
-
1. 下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在 中,若 , ,则 的度数为( )A、65° B、70° C、75° D、80°3. 已知三角形两边的长分别是1和5,则此三角形第三边的长可能是( )A、4 B、5 C、6 D、74. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是( )
2. 在 中,若 , ,则 的度数为( )A、65° B、70° C、75° D、80°3. 已知三角形两边的长分别是1和5,则此三角形第三边的长可能是( )A、4 B、5 C、6 D、74. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是( ) A、SSS B、SAS C、AAS D、ASA5. 如图,在△ABC中,AB的垂直平分线交AB于点D , 交BC于点E , 若BC=6,AC=5,则△ACE的周长为( )
A、SSS B、SAS C、AAS D、ASA5. 如图,在△ABC中,AB的垂直平分线交AB于点D , 交BC于点E , 若BC=6,AC=5,则△ACE的周长为( ) A、8 B、11 C、16 D、176. 一个多边形的每一个外角都是45°,则这个多边形的边数为( )A、6 B、7 C、8 D、97. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、8 B、11 C、16 D、176. 一个多边形的每一个外角都是45°,则这个多边形的边数为( )A、6 B、7 C、8 D、97. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )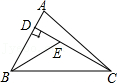 A、10 B、7 C、5 D、48. 一个凸多边形的内角和比它的外角和的 3 倍还多 180°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形9. 如图,CD⊥AB , BE⊥AC , 垂足分别为点D , 点E , BE、CD相交于点O . ∠1=∠2,则图中全等三角形共有( )
A、10 B、7 C、5 D、48. 一个凸多边形的内角和比它的外角和的 3 倍还多 180°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形9. 如图,CD⊥AB , BE⊥AC , 垂足分别为点D , 点E , BE、CD相交于点O . ∠1=∠2,则图中全等三角形共有( ) A、2对 B、3对 C、4对 D、5对10. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A、2对 B、3对 C、4对 D、5对10. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )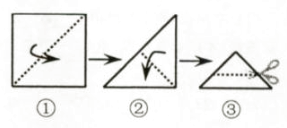 A、
A、 B、
B、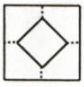 C、
C、 D、
D、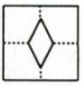 11. 如图,∠ACD是△ABC的外角,∠BAC=80°,∠ABC和∠ACD的平分线相交于点E , 连接AE , 则∠CAE的度数是( )
11. 如图,∠ACD是△ABC的外角,∠BAC=80°,∠ABC和∠ACD的平分线相交于点E , 连接AE , 则∠CAE的度数是( ) A、35° B、40° C、50° D、55°12. 如图,△ABC中,∠BAC=90°,AB=AC、BM是AC边的中线,有AD⊥BM;垂足为点E交BC于点D . 且AH平分∠BAC交BM于N . 交BC于H . 连接DM . 则下列结论:①∠AMB=∠CMD;②HN=HD;③BN=AD;④∠BNH=∠MDC;错误的有( )个.
A、35° B、40° C、50° D、55°12. 如图,△ABC中,∠BAC=90°,AB=AC、BM是AC边的中线,有AD⊥BM;垂足为点E交BC于点D . 且AH平分∠BAC交BM于N . 交BC于H . 连接DM . 则下列结论:①∠AMB=∠CMD;②HN=HD;③BN=AD;④∠BNH=∠MDC;错误的有( )个.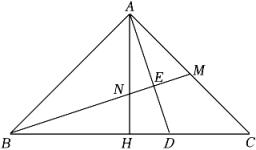 A、0 B、1 C、3 D、4
A、0 B、1 C、3 D、4二、填空题(本大题共6小题,共18分)
-
13. 一个等腰三角形的两边长分别为2和5,则它的周长为。14. 在平面直角坐标系中,点M(a , 3)与点N(5,b)关于y轴对称,则a﹣b= .15. 如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为.
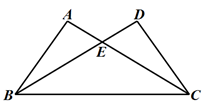 16. 如图,∠A+∠B+∠C+∠D+∠E= .
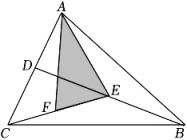
16. 如图,∠A+∠B+∠C+∠D+∠E= .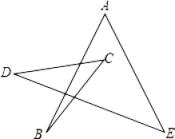 17. 如图,BD是△ABC的中线,点E , F分别为BD , CE的中点,若△ABC的面积为12.则△AEF的面积是 .
17. 如图,BD是△ABC的中线,点E , F分别为BD , CE的中点,若△ABC的面积为12.则△AEF的面积是 .
 18. 如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCED的外部时,∠1=72°,∠2=26°,则∠A= .
18. 如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BCED的外部时,∠1=72°,∠2=26°,则∠A= .
三、解答题(本大题共6小题,共46分)
-
19. 如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
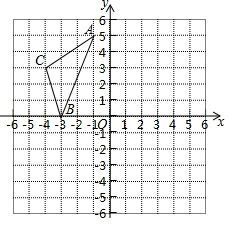 (1)、在图中作出△ABC关于y轴对称的图形△A1B1C1;(2)、写出点A1 , B1 , C1的坐标;(3)、求△ABC的面积.20. 如图,在△ABC中,AD平分∠BAC , P为线段AD上的一个动点,PE⊥AD交直线BC于点E , 若∠B=35°,∠ACB=85°.
(1)、在图中作出△ABC关于y轴对称的图形△A1B1C1;(2)、写出点A1 , B1 , C1的坐标;(3)、求△ABC的面积.20. 如图,在△ABC中,AD平分∠BAC , P为线段AD上的一个动点,PE⊥AD交直线BC于点E , 若∠B=35°,∠ACB=85°.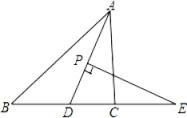 (1)、求∠DAC的度数;(2)、求∠E的度数.21. 如图,已知点B , C , F , E在同一直线上,∠1=∠2,BF=CE , AB∥DE . 求证:△ABC≌△DEF .
(1)、求∠DAC的度数;(2)、求∠E的度数.21. 如图,已知点B , C , F , E在同一直线上,∠1=∠2,BF=CE , AB∥DE . 求证:△ABC≌△DEF .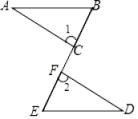 22. 如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O , AC=AE , AD=AB , ∠BAC=∠DAE .
22. 如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O , AC=AE , AD=AB , ∠BAC=∠DAE . (1)、求证:△ABC≌△ADE;(2)、若∠BAD=20°,求∠CDE的度数.23. 如图,∠ACB=90°,AC=BC , AD⊥CE , BE⊥CE , 垂足分别为D , E .
(1)、求证:△ABC≌△ADE;(2)、若∠BAD=20°,求∠CDE的度数.23. 如图,∠ACB=90°,AC=BC , AD⊥CE , BE⊥CE , 垂足分别为D , E . (1)、证明:△BCE≌△CAD;(2)、若AD=25cm , BE=8cm , 求DE的长.24. 八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(1)、证明:△BCE≌△CAD;(2)、若AD=25cm , BE=8cm , 求DE的长.24. 八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧. (1)、【阅读理解】如图1,在△ABC中,若AB=10,BC=8.求AC边上的中线BD的取值范围.小聪同学是这样思考的;延长BD至E , 使DE=BD , 连接CE . 利用全等将边AB转化到CE , 在△BCE中利用三角形三边关系即可求出中线BD的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是:;中线BD的取值范围是 .(2)、【理解与应用】如图2,在△ABC中,∠B=90°,点D是AC的中点,点M在AB边上,点N在BC边上,若DM⊥DN . 试猜想线段AM、CN、MN三者之间的数量关系,并证明你的结论.(3)、【问题解决】如图3,在△ABC中,点D是AC的中点,AB=MB , BC=BN , 其中∠ABM=∠NBC=90°,连接MN , 探索BD与MN的关系,并说明理由.
(1)、【阅读理解】如图1,在△ABC中,若AB=10,BC=8.求AC边上的中线BD的取值范围.小聪同学是这样思考的;延长BD至E , 使DE=BD , 连接CE . 利用全等将边AB转化到CE , 在△BCE中利用三角形三边关系即可求出中线BD的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是:;中线BD的取值范围是 .(2)、【理解与应用】如图2,在△ABC中,∠B=90°,点D是AC的中点,点M在AB边上,点N在BC边上,若DM⊥DN . 试猜想线段AM、CN、MN三者之间的数量关系,并证明你的结论.(3)、【问题解决】如图3,在△ABC中,点D是AC的中点,AB=MB , BC=BN , 其中∠ABM=∠NBC=90°,连接MN , 探索BD与MN的关系,并说明理由.