山东省青岛市城阳区2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列各数是无理数的是( )A、 B、 C、 D、52. 若的三边分别是 , , , 则下列条件能判断是直角三角形的是( )A、 B、 C、 , , D、 , ,3. 下列计算正确的是( )A、 B、 C、 D、4. 下列几组数中,为勾股数的是( )A、1,2,3 B、3,4,6 C、5,12,13 D、 , ,5. 下列各点在一次函数的图象上的是( )A、 B、 C、 D、6. 如图,分别以的三边为直径向外作半圆,斜边 , 则图中阴影部分的面积为( )
 A、 B、 C、 D、7. 已知点 , 都在直线上,则 , 大小关系是( )A、 B、 C、 D、不能比较8. 若 , 则的值为( )A、 B、 C、25 D、59. 《九章算术》是古代东方数学代表作,汇集了我国历代学者的劳动和智慧,被誉为人类科学史上应用数学的“算经之首”.其中记录了这样一个问题,如图,这个问题的大意是:有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面.则这根芦苇的长度为( )
A、 B、 C、 D、7. 已知点 , 都在直线上,则 , 大小关系是( )A、 B、 C、 D、不能比较8. 若 , 则的值为( )A、 B、 C、25 D、59. 《九章算术》是古代东方数学代表作,汇集了我国历代学者的劳动和智慧,被誉为人类科学史上应用数学的“算经之首”.其中记录了这样一个问题,如图,这个问题的大意是:有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面.则这根芦苇的长度为( )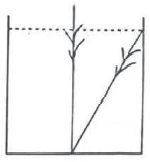 A、10尺 B、12尺 C、13尺 D、14尺10. 一次函数与正比例函数( , 是常数,且)在同一平面直角坐标系中的图象可能是( )A、
A、10尺 B、12尺 C、13尺 D、14尺10. 一次函数与正比例函数( , 是常数,且)在同一平面直角坐标系中的图象可能是( )A、 B、
B、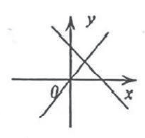 C、
C、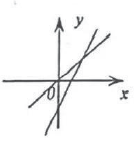 D、
D、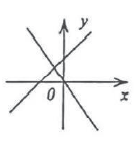
二、填空题(本大题共6小题,每小题3分,共18分)
-
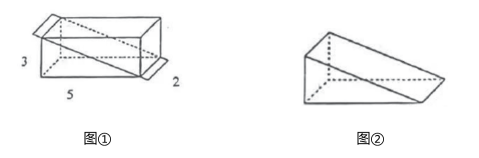
11. (结果精确到1).12. 如图①,用一个平面截长方体,得到如图②的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.若长方体的长、宽、高分别为5,2,3,则图①中截面的面积为 .
 13. 一次函数的图象不经过第象限.14. 如图,已知 . 则点A所表示的数是 .
13. 一次函数的图象不经过第象限.14. 如图,已知 . 则点A所表示的数是 .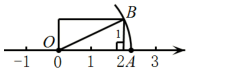 15. 如图,将直线向上平移2个单位,得到一个一次函数的图象,则这个一次函数的表达式为 .
15. 如图,将直线向上平移2个单位,得到一个一次函数的图象,则这个一次函数的表达式为 .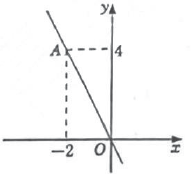 16. 如图,长方体的底面边长分别为和 , 高为 . 如果用一根细线从点开始经过4个侧面缠绕1圈到达点 , 那么所用细线最短需要;如果从点开始经过4个侧面缠绕2圈到达点 , 那么所用细线最短需要 .
16. 如图,长方体的底面边长分别为和 , 高为 . 如果用一根细线从点开始经过4个侧面缠绕1圈到达点 , 那么所用细线最短需要;如果从点开始经过4个侧面缠绕2圈到达点 , 那么所用细线最短需要 .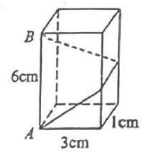
三、解答题(本大题共6小题,共72分)
-
17. 计算:(1)、;(2)、;(3)、;(4)、 .18. 已知的算术平方根是 , 的平方根是 , 是的整数部分,求的平方根.19. 如图,猴山的坐标为 , 孔雀园的坐标为 .
 (1)、车站的坐标为 .(2)、现有一个厕所的位置记为 , 且与猴山的距离为5,则的值为 .20. 根据表格解答下列问题:
(1)、车站的坐标为 .(2)、现有一个厕所的位置记为 , 且与猴山的距离为5,则的值为 .20. 根据表格解答下列问题:13
13.1
13.2
13.3
13.4
13.5
13.6
13.7
13.8
13.9
14
169
171.61
174.24
176.89
179.56
182.25
184.96
187.69
190.44
193.21
196
(1)、的平方根是;(2)、;(3)、若 , 则满足条件的整数的值是 .21. 在平面直角坐标系中描出下列各点,并将这些点依次用线段连接., , .
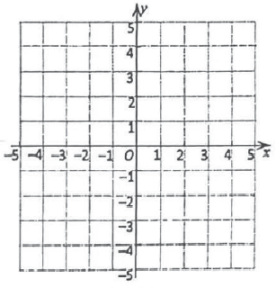 (1)、观察得到的图形,它位于第象限;(2)、将上面各点的纵坐标不变,横坐标分别乘 , 按同样的方法将所得各点连接起来(画出符合题意的图形).所得图形与原图形的位置关系是;(3)、的高线的长为 . (请直接写出答案,结果化成最简形式)22. 自2019年1月1日起,我国居民个人劳务报酬所得税预扣税缴税款的计算方法是:每次收入不超过800元的,预扣预缴税款为0;每次收入超过800元但不超过4000元的,预扣预缴税款;……如某人取得劳务报酬2000元,他这笔所得应预缴税款(元).(1)、当每次收入超过800元但不超过4000元时,写出劳务报酬所得税预扣预缴税款(元)与每次收入(元)之间的关系式;(2)、某人某次取得劳务报酬2400元,他这笔所得应预扣预缴税款多少元?(3)、如果某人某次预扣预缴劳务报酬所得税560元,那么此人这次取得劳务报酬是多少元?23. 如图,平面直角坐标系中,点的坐标为 , 过点作轴,轴,点为轴上一点,将沿直线折叠,点落在边上的点处.
(1)、观察得到的图形,它位于第象限;(2)、将上面各点的纵坐标不变,横坐标分别乘 , 按同样的方法将所得各点连接起来(画出符合题意的图形).所得图形与原图形的位置关系是;(3)、的高线的长为 . (请直接写出答案,结果化成最简形式)22. 自2019年1月1日起,我国居民个人劳务报酬所得税预扣税缴税款的计算方法是:每次收入不超过800元的,预扣预缴税款为0;每次收入超过800元但不超过4000元的,预扣预缴税款;……如某人取得劳务报酬2000元,他这笔所得应预缴税款(元).(1)、当每次收入超过800元但不超过4000元时,写出劳务报酬所得税预扣预缴税款(元)与每次收入(元)之间的关系式;(2)、某人某次取得劳务报酬2400元,他这笔所得应预扣预缴税款多少元?(3)、如果某人某次预扣预缴劳务报酬所得税560元,那么此人这次取得劳务报酬是多少元?23. 如图,平面直角坐标系中,点的坐标为 , 过点作轴,轴,点为轴上一点,将沿直线折叠,点落在边上的点处. (1)、请你直接写出点的坐标;(2)、求 , 的长;(3)、求四边形的面积.24.
(1)、请你直接写出点的坐标;(2)、求 , 的长;(3)、求四边形的面积.24.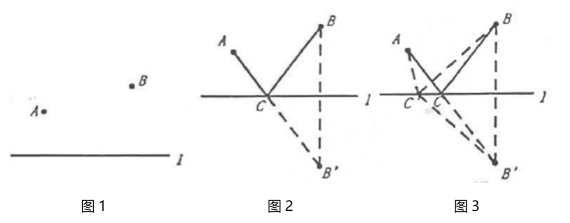
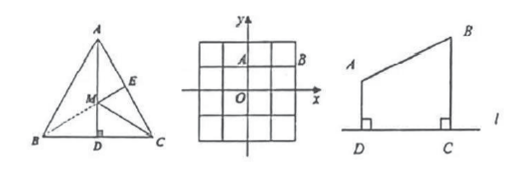
提出问题:早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者——海伦.一天,一位将军专程拜访他,请教一个百思不得其解的问题:如图1,将军每天从军营出发,先到河边饮马,然后再去军营开会,怎样走才能使路程最短?据说海伦略加思索就解决了它.这个问题被称为“将军饮马”的问题.你知道海伦是怎样解决这个问题的吗?
(1)、研究方法:第一步作其中一定点的对称点,第二步连接对称点和另一定点,第三步找与河(对称轴)的交点.如图2,此时最短,由轴对称的性质可得 , 所以最短.如图3,在直线上任取点 , 的理由是: .(2)、如图4,在等边 , , , 是的中点,是上的一点,则的最小值是;(请直接写出答案)(3)、如图5,在平面直角坐标系中,已知点 , 点 , 点在轴上运动,当的值最小时,点的坐标是;(请直接写出答案)(4)、如图6,于点 , 于点 , 且 , , 当点在直线上运动时,的最小值是 . (请直接写出答案)25. 如图,一次函数的图象过点 , , 与轴相交于点 , 过点作轴,垂足为 .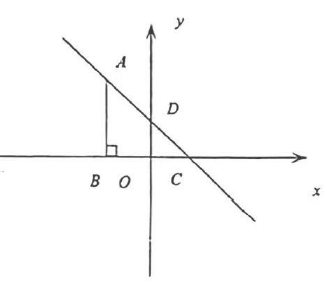 (1)、求一次函数的表达式;(2)、求一次函数的图象与两坐标轴围成的三角形的面积;(3)、已知在轴上有点 , 满足是等腰三角形,请你直接写出所有符合条件的点的坐标.
(1)、求一次函数的表达式;(2)、求一次函数的图象与两坐标轴围成的三角形的面积;(3)、已知在轴上有点 , 满足是等腰三角形,请你直接写出所有符合条件的点的坐标.