上海市奉贤区2023-2024学年八年级上学期数学期中考试试卷

试卷更新日期：2023-12-13 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列各式中，二次根式 $\sqrt{a - b}$ 的有理化因式是（）

A、 $\sqrt{a+b}$ B、 $\sqrt{a} + \sqrt{b}$ C、 $\sqrt{a - b}$ D、 $\sqrt{a} - \sqrt{b}$

查看试题解析
2. 下列根式中，是最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt[3]{2}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
3. 下列一元二次方程中，有实数根的是（）

A、 $x^{2} + 3 = 0$ B、 $x^{2} - x + 3 = 0$ C、 $x^{2} + x + 3 = 0$ D、 $x^{2} - x - 3 = 0$

查看试题解析
4. 如果关于 $x$ 的方程 $(a - 1) x^{2} - 2 x + a^{2} - 1 = 0$ 有一个根是0，那么 $a$ 的值是（）

A、1或 $- 1$ B、1 C、 $- 1$ D、0

查看试题解析
5. 下列各式中，一定成立的是（）

A、 $\sqrt[]{{(a + b)}^{2}} = a + b$ B、 $\sqrt[]{{(a^{2} + 1)}^{2}} = a^{2} + 1$ C、 $\sqrt[]{a^{2} - 1} = \sqrt{a + 1} \cdot \sqrt{a - 1}$ D、 $\sqrt{\frac{a}{b}} = \frac{1}{b} \sqrt{a b}$

查看试题解析
6. 等腰 $Δ A B C$ 的一边长为4，另外两边的长是关于x的方程 $x^{2} - 10 x + m = 0$ 的两个实数根，则等腰三角形底边的值是（）

A、4 B、25 C、4或6 D、24或25

查看试题解析

二、填空题

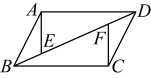
7. 如果 $\sqrt{x - 1}$ 有意义，那么x的取值范围为．

查看试题解析
8. 计算： $\sqrt{{(- 3)}^{2}}$ = ．

查看试题解析
9. 计算： $\sqrt{2} \cdot \sqrt{6} \div \sqrt{3} =$ ．

查看试题解析
10. 若最简二次根式 $\sqrt{4 + 2 a}$ 与 $\sqrt{1 - a}$ 是同类二次根式，则 $a =$ ．

查看试题解析
11. 一元二次方程 $x^{2} - 3 x + \sqrt{5} = 0$ 的一次项系数是．

查看试题解析
12. 方程x²=3x的根是．

查看试题解析
13. 不等式 $x < \sqrt{2} x - 1$ 的解集是．

查看试题解析
14. 若方程 $(n + 1) x^{2} - 4 x + 5 = 0$ 是关于 $x$ 的一元二次方程，则 $n$ ．

查看试题解析
15. 如果关于 $x$ 的一元二次方程 $2 x^{2} + m x + 1 = 0$ 的一个根为1，那么多项式 $2 x^{2} + m x + 1$ 可分解为．

查看试题解析
16. 已知关于x的方程 $(k - 2) x^{2} - x + 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值范．

查看试题解析
17. 某厂工业废气年排放量为450万立方米，为了改善上海市的大气环境质量，决定分二期投入治理，使废气的年排放量减少到288万立方米，如果每期治理中废气减少的百分率相同，每期减少的百分率是．

查看试题解析
18. 在 $△ A B C$ 中，点O与点A、B、C的距离都相等， $∠ A = 80 °$ ，那么 $∠ B O C$ 等于．

查看试题解析
19. 在 $△ A B C$ 中， $A H$ 是高，如果 $∠ B = 2 ∠ C$ ， $B H = 3$ ， $B C = 12$ ，那么 $A B$ 的长为．

查看试题解析
20. 如图， $A E = C F$ ， $A D = B C$ ， E、F为 $B D$ 上的两点，且 $B F = D E$ ，若 $∠ A E D = 66 °$ ， $∠ A D B = 24 °$ ，则 $∠ B C F$ 的度数为．

查看试题解析

三、解答题

21. 计算题

(1)、计算： $\sqrt{12} - \sqrt{18} - \sqrt{0.5} + \sqrt{\frac{1}{3}}$ ；

(2)、计算： $\frac{2}{b} \sqrt{a b} \cdot (- \frac{3}{2} \sqrt{a^{3} b}) \div \frac{1}{3} \sqrt{\frac{b}{a}} (a > 0)$ ；

查看试题解析
22. 解方程

(1)、（用配方法） $2 x^{2} - 4 x - 1 = 0$ ；

(2)、 ${(x + 3)}^{2} - 2 (x + 3) - 8 = 0$

查看试题解析
23. 先化简，再求值：已知 $x = \frac{1}{3 + 2 \sqrt{2}}$ ，求 $\frac{{(2 - x)}^{2}}{x - 2} + \frac{\sqrt{x^{2} + 9 - 6 x}}{x - 3}$ 的值

查看试题解析
24. 某商店购进一种商品，单价30元，试销中发现这种商品每天的销售量ρ（件）与每件的销售价x（元）满足关系： $ρ$ =100-2x．若商店每天销售这种商品要获得200元的销售利润，那么每件商品的售价应定为多少元?每天要售出这种商品多少件?

查看试题解析
25. 如图，点D是线段 $B C$ 的中点， $A D ⊥ B C$ ，点P是线段 $A D$ 上的一点，射线 $B P$ 交边 $A C$ 于点E ， $E H ⊥ A B$ 于点H ，过B作 $B F ⊥ A C$ 于点F ．

(1)、求证： $∠ B A D = ∠ C B F$ ；

(2)、如果 $P D = B D$ ，求证： $E F = E H$ ．

查看试题解析
26. 如图，在 $△ A B C$ 中， $A B = A C ， A D$ 是 $△ A B C$ 的中线，点E在 $A D$ 上，点F在 $B A$ 的延长线上， $E F$ 与 $A C$ 交于点O ，且 $E C = E F$ ．

(1)、求证： $∠ C E F = ∠ C A F$ ；

(2)、若 $∠ B = 30 °$ ，求证： $A B = A E + A F$

查看试题解析