上海市虹口区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、单选题
-
1. 下列各组图形中,一定相似的是( )A、两个矩形 B、两个菱形 C、两个正方形 D、两个等腰三角形2. 如果5x=6y,那么下列结论正确的是( )A、 B、 C、 D、3. 符号tanA表示( )A、∠A的正弦 B、∠A的余弦 C、∠A的正切 D、∠A的余切4. 已知 , 下列说法中,不正确的是( )A、 B、与方向相同 C、 D、5. 如图,在△ABC中,点D、E分别在边AB、AC的反向延长线上,下面比例式中,不能判定ED//BC的是( )
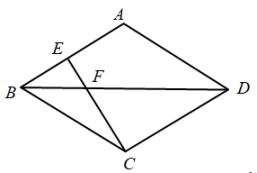
 A、 B、 C、 D、6. 如图,四边形是平行四边形,的平分线交于 , 交于 , 交的延长线于 . 那么下列结论正确的是( )
A、 B、 C、 D、6. 如图,四边形是平行四边形,的平分线交于 , 交于 , 交的延长线于 . 那么下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 在比例尺为的地图上,某两地图距为3厘米,则这两地的实际距离是千米.8. 已知线段 , 是线段的黄金分割点 , 则 .9. 已知向量与单位向量方向相反,且 , 那么= (用向量的式子表示)10. 化简:2(+)﹣(﹣)= .11. 如果两个相似三角形的周长之比1:4,那么它们的某一对对应角的角平分线之比为 .12. 如图,在 , 点分别在的两边上,且 , 如果 , 那么线段的长是 .
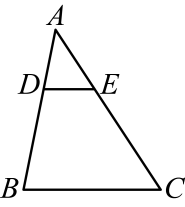 13. 如图,已知 , 它们依次交直线于点和点 . 如果 , 那么线段的长是 .
13. 如图,已知 , 它们依次交直线于点和点 . 如果 , 那么线段的长是 .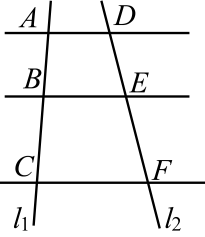 14. 如图,△ABC中,点D在边AC上,∠ABD=∠C,AD=9,DC=7,那么AB= .
14. 如图,△ABC中,点D在边AC上,∠ABD=∠C,AD=9,DC=7,那么AB= . 15. 如图,在中,垂足为点D , 是边上的中线,与相交于点G , 则的长为 .
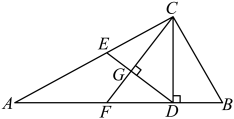
15. 如图,在中,垂足为点D , 是边上的中线,与相交于点G , 则的长为 .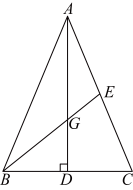 16. 如图,梯形中, , 点在边上,且 , 则的面积与四边形的面积之比为 .
16. 如图,梯形中, , 点在边上,且 , 则的面积与四边形的面积之比为 . 17. 将绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得 , 如图①,我们将这种变换记为 , 如图②,在中, , 如果对作变换得 , 使点B , C , B′在同一直线上,且 , 那么 .
17. 将绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得 , 如图①,我们将这种变换记为 , 如图②,在中, , 如果对作变换得 , 使点B , C , B′在同一直线上,且 , 那么 .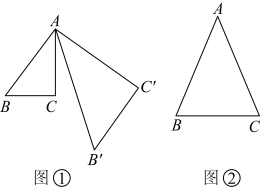 18. 如图,在矩形ABCD中,E、F、G分别是边AB、BC、AD上点,且∠FEG=90°,EG=6,GF与AC交于点M , 若= , 则MF= .
18. 如图,在矩形ABCD中,E、F、G分别是边AB、BC、AD上点,且∠FEG=90°,EG=6,GF与AC交于点M , 若= , 则MF= .
三、解答题
-
19. 已知求:的值.20. 如图,在梯形中, , , 对角线相交于点 , 设 .
 (1)、用的式子表示向量 . , ;(2)、在图中作出向量在方向上的分向量,并写出结论.21. 如图,已知在梯形ABCD中,AD∥BC , ∠ABD=∠C , AD=4,BC=9,锐角∠DBC的正弦值为 . 求:
(1)、用的式子表示向量 . , ;(2)、在图中作出向量在方向上的分向量,并写出结论.21. 如图,已知在梯形ABCD中,AD∥BC , ∠ABD=∠C , AD=4,BC=9,锐角∠DBC的正弦值为 . 求: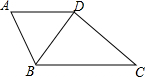 (1)、对角线BD的长;(2)、梯形ABCD的面积.22. 如图,在中,点分别在边上, , 垂足为点 , , 垂足为点 .
(1)、对角线BD的长;(2)、梯形ABCD的面积.22. 如图,在中,点分别在边上, , 垂足为点 , , 垂足为点 .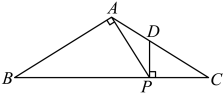 (1)、求证:;(2)、如果 , 求的长.
(1)、求证:;(2)、如果 , 求的长.