上海市黄浦区2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2023-12-13 类型：期中考试

进入出卷网下载

一、单选题

1. 如果 $5 x = 3 y$ （x、y均不为零），那么 $x ： y$ 的值是（）

A、 $\frac{5}{3}$ B、 $\frac{3}{5}$ C、 $\frac{3}{8}$ D、 $\frac{5}{8}$

查看试题解析
2. 已知Rt△ABC中，∠C=90°，∠CAB=α，AC=7，那么BC为（　　）

A、7sinα B、7cosα C、7tanα D、7cotα

查看试题解析
3. 在△ABC中，点D、E分别在AB、AC上，如果AD=2，BD=3，那么由下列条件能够判定DE∥BC的是（　　）

A、 $\frac{D E}{B C}$ = $\frac{2}{3}$ B、 $\frac{D E}{B C}$ = $\frac{2}{5}$ C、 $\frac{A E}{A C}$ = $\frac{2}{3}$ D、 $\frac{A E}{A C}$ = $\frac{2}{5}$

查看试题解析
4. 下列命题正确的是（　　）

A、如果| $\vec{a}$ |＝| $\vec{b}$ |，那么 $\vec{a}$ ＝ $\vec{b}$ B、如果 $\vec{a}$ 、 $\vec{b}$ 都是单位向量，那么 $\vec{a}$ ＝ $\vec{b}$ C、如果 $\vec{a}$ ＝k $\vec{b}$ （k≠0），那么 $\vec{a}$ ∥ $\vec{b}$ D、如果m＝0或 $\vec{a}$ ＝ $\vec{0}$ ，那么m $\vec{a}$ ＝0

查看试题解析
5. 如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△_DOE：S_△_COA=1：25，则S_△_BDE与S_△_CDE的比是（　　）

A、1：3 B、1：4 C、1：5 D、1：25

查看试题解析
6. 如图， $D$ 是 $△ A B C$ 边 $B C$ 上的一点， $∠ B A D = ∠ C ， ∠ A B C$ 的平分线交边 $A C$ 于点 $E$ ，交 $A D$ 于点 $F$ ，则图中一定相似三角形有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析

二、填空题

7. 如果 $x ： y = 5 ： 3$ ，那么 $\frac{x - y}{y} =$ ．

查看试题解析
8. 如果在比例尺为1：1000000的地图上， $A$ ， $B$ 两地的图上距离是1.6厘米，那么 $A$ 、 $B$ 两地的实际距离是千米．

查看试题解析
9. 若Q是线段MN延长线上一点，已知 $\vec{M N}$ ＝ $\vec{a}$ ， $\vec{Q N}$ ＝ $\vec{b}$ ，则 $\vec{M Q}$ ＝．（用含 $\vec{a}$ 、 $\vec{b}$ 表示）

查看试题解析
10. 设点P是线段 $A B$ 的黄金分割点 $(A P < B P)$ ， $A B = 2$ 厘米，那么线段 $B P$ 的长是厘米．

查看试题解析
11.
如图，直线AD∥BE∥CF， $B C = \frac{2}{3} A B$ ， DE=6，那么EF的值是．

查看试题解析
12. 已知点G是等腰直角三角形 $A B C$ 的重心， $A C = B C = 6$ ，那么AG的长为．

查看试题解析
13. 如图，小红晚上由路灯 $A$ 下的 $B$ 处走到 $C$ 处时，测得影子 $C D$ 的长为1米，继续往走2.5米到达 $E$ 处时，测得影子 $E F$ 的长为2米，已知小明的身高是1.5米，那么路灯 $A$ 离地面的高度 $A B$ 的长为米．

查看试题解析
14. 如图，四边形DEFG是△ABC的内接矩形，其中D、G分别在边AB，AC上，点E、F在边BC上，DG=2DE，AH是△ABC的高，BC=20，AH=15，那么矩形DEFG的周长是．

查看试题解析
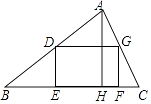15. 边长分别为10，6，4的三个正方形拼接在一起，它们的底边在同一直线上（如图），则图中阴影部分的面积为．

查看试题解析
16. 如图已知在 $△ A B C$ 中， $∠ C = 90 ° ， A B = 5 ， c o t B = \frac{1}{2}$ ，正方形 $D E F G$ 的顶点 $G 、 F$ 分别在边 $A C 、 B C$ 上，点 $D 、 E$ 在斜边 $A B$ 上，那么正方形 $D E F G$ 的边长为．

查看试题解析
17. 新定义：将一个凸四边形分成一个等腰三角形和一个等腰直角三角形的对角线叫做这个四边形的“等腰直角线”．已知一个直角梯形的“等腰直角线”等于4，它的面积是．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是 $△ A B C$ 的角平分线， $A C ： B C = 3 ： 4$ ．将 $R t △ A B C$ 绕点A旋转，如果点 $C$ 落在射线 $C D$ 上，点 $B$ 落在点 $E$ 处，连接 $D E$ ，那么 $∠ A E D$ 的正切值为．

查看试题解析

三、解答题

19. 计算： $\frac{2 s i n 30 °}{2 c o s 45 ° - t a n 45 °} + | c o t 30 ° - 1 |$ ．

查看试题解析
20. 如图，已知平行四边形ABCD ，点M、N是边DC、BC的中点，设 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ．

(1)、求向量 $\vec{M N}$ ；

(2)、在图中求作向量 $\vec{M N}$ 在 $\vec{A B}$ 、 $\vec{A D}$ 方向上的分向量．（不要求写作法，但要指出所作图中表示结论的向量）．

查看试题解析
21. 已知：如图，在△ABC中，AB＝13，AC＝8，cos∠BAC＝ $\frac{5}{13}$ ， BD⊥AC，垂足为点D，E是BD的中点，连接AE并延长，交边BC于点F．

(1)、求∠EAD的余切值；

(2)、求 $\frac{B F}{C F}$ 的值．

查看试题解析
22. 如图，在 $△ A B C$ 中，点D、E分别在边 $A B$ 、 $A C$ 上，连接 $D E$ 、 $B E$ ， $∠ A B E = ∠ A E D$ ， $\frac{D E}{B E} = \frac{B D}{C E}$ ．

(1)、求证： $D E ∥ B C$ ；

(2)、若 $S_{△ A D E} = 1$ ， $S_{四边形 D B C E} = 8$ ，求 $△ B D E$ 的面积．

查看试题解析
23. 如图，四边形 $A B C D$ 是平行四边形， $A E ⊥ B C$ 于 $E$ ， $A F ⊥ C D$ 于 $F$ ．求证：

(1)、 $△ A B E ∽ △ A D F$ ；

(2)、 $C D \cdot E F = A C \cdot A E$ ．

查看试题解析
24. 已知：如图， $△ A B C$ 各顶点的坐标分别是 $A (0 ， - 4) 、 B (- 2 ， 0) 、 C (4 ， 0)$ ．

(1)、求 $∠ B A C$ 的余切值；

(2)、若点 $P$ 在 $y$ 轴的正半轴，且 $△ P O C$ 与 $△ A O B$ 相似，请直接写出点 $P$ 的坐标；

(3)、已知点 $M$ 在 $y$ 轴上，如果 $∠ O M B - ∠ O A B = ∠ A C B$ ，求点 $M$ 的坐标．

查看试题解析
25. 已知：如图，在矩形 $A B C D$ 中， $A B = 3 ， A D = 4 ， E$ 是对角线 $B D$ 上一点（与 $B 、 D$ 不重合）， $E F$ 平分 $∠ A E D$ 交边 $A D$ 于点 $F ， F G ⊥ A E$ ，交 $A E$ 于点 $G$ ．

(1)、当 $E F ⊥ A D$ 时，求 $E F$ 的长；

(2)、当 $△ A F G$ 与 $△ B C D$ 相似时，求 $∠ D E F$ 的正切值；

(3)、如果 $△ D E F$ 的面积是 $△ E F G$ 面积的2倍，求 $B E$ 的长．

查看试题解析