上海市闵行区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、单选题
-
1. 将图形甲通过放大得到图形乙,那么在图形甲与图形乙的对应量中,没有被放大的是( )A、边的长度 B、图形的周长 C、图形的面积 D、角的度数2. 小明有一张上海市地图,地图的比例尺是 , 如果A , B两地在地图上的距离是4厘米,那么A , B两地的实际距离是( )A、8千米 B、0.8千米 C、0.08千米 D、0.008千米3. 已知是非零向量,如果与同方向的单位向量记作 , 那么下列式子中正确的是( )A、 B、 C、 D、4. 在中, , a , b , c分别表示的对边,那么下列结论中错误的是( )A、 B、 C、 D、5. 如图,点D、E、F分别在的边上,且 , , 下列4个式子中,不正确的是( )
 A、 B、 C、 D、6. 在平面直角坐标系中,已知点 , 点 , , , 点D在第一象限内,如果以点D、O、C为顶点的三角形与相似,那么这样的点D有( )个A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、6. 在平面直角坐标系中,已知点 , 点 , , , 点D在第一象限内,如果以点D、O、C为顶点的三角形与相似,那么这样的点D有( )个A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 若 , 那么 .8. 已知线段b是线段a , c的比例中项, , , 那么cm.9. 已知点D是的边的黄金分割点, , 作交边于点E , 那么 .10. 如图, , , , , 那么 .
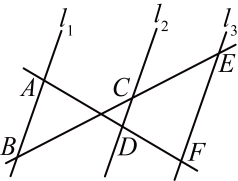 11. 已知,点D , E分别在的 , 边上,且 , 与相交于点F . 如果 , 那么的值是 .12. 在中, , , 如果 , 那么 .13. 已知两个矩形相似,第一个矩形的两边长分别是3和4,第二个矩形较短的一边长是4,那么第二个矩形较长的一边长是 .14. 如图,经过的重心,设 , , 那么可以用向量 , 表示为: .
11. 已知,点D , E分别在的 , 边上,且 , 与相交于点F . 如果 , 那么的值是 .12. 在中, , , 如果 , 那么 .13. 已知两个矩形相似,第一个矩形的两边长分别是3和4,第二个矩形较短的一边长是4,那么第二个矩形较长的一边长是 .14. 如图,经过的重心,设 , , 那么可以用向量 , 表示为: .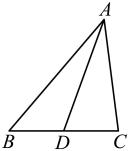 15. 如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米.那么斜面AB的坡度为 .
15. 如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米.那么斜面AB的坡度为 .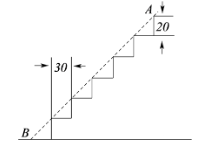 16. 如图,某时刻阳光通过窗口AB照射到室内,在地面上留下4米宽的“亮区”DE,光线与地面所成的角(如∠BEC)的正切值是 , 那么窗口的高AB等于米.
16. 如图,某时刻阳光通过窗口AB照射到室内,在地面上留下4米宽的“亮区”DE,光线与地面所成的角(如∠BEC)的正切值是 , 那么窗口的高AB等于米.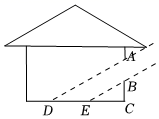 17. 如图,在中, , 四边形 , , 均为正方形,P , G , N在BC边上,点E , H , P在AB边上.如果 , , 那么正方形的面积为 .
17. 如图,在中, , 四边形 , , 均为正方形,P , G , N在BC边上,点E , H , P在AB边上.如果 , , 那么正方形的面积为 .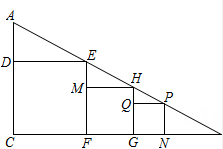 18. 如图,在中, , , 点M , N分别在边上,将沿直线翻折,点C恰好落在边上,记为点 , 如果与相似,那么折痕的长为 .
18. 如图,在中, , , 点M , N分别在边上,将沿直线翻折,点C恰好落在边上,记为点 , 如果与相似,那么折痕的长为 .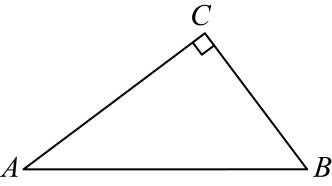
三、解答题
-
19. 计算:20. 如图,在中, , , 分别是边上的中线和高, , , 求 , 的长.
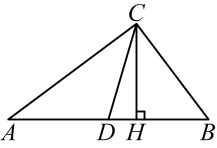 21. 已知:如图,平行四边形中,点M、N分别在边、上,对角线分别交、于点E、F , 且 .
21. 已知:如图,平行四边形中,点M、N分别在边、上,对角线分别交、于点E、F , 且 . (1)、求证:;(2)、设 , , 请直接写出和关于、的分解式:; .22. 如图,海中有一小岛P , 在以P为圆心,半径为海里的圆形海域内有暗礁.一轮船自西向东航行,它在A处测得小岛P位于北偏东方向上,且A , P之间的距离为32海里.
(1)、求证:;(2)、设 , , 请直接写出和关于、的分解式:; .22. 如图,海中有一小岛P , 在以P为圆心,半径为海里的圆形海域内有暗礁.一轮船自西向东航行,它在A处测得小岛P位于北偏东方向上,且A , P之间的距离为32海里.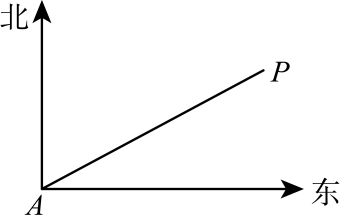 (1)、若轮船继续向正东方向航行,轮船有无触礁危险?(2)、如果轮船继续向正东方向航行有危险,轮船自A处开始改变航行方向,沿南偏东度方向航行确保安全通过这一海域,求的取值范围.23. 如图,在梯形中, , , 点E是边中点,连接并延长交的延长线于点F , , 且 .
(1)、若轮船继续向正东方向航行,轮船有无触礁危险?(2)、如果轮船继续向正东方向航行有危险,轮船自A处开始改变航行方向,沿南偏东度方向航行确保安全通过这一海域,求的取值范围.23. 如图,在梯形中, , , 点E是边中点,连接并延长交的延长线于点F , , 且 .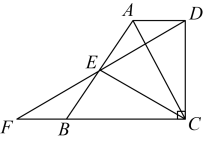 (1)、求证:;(2)、求证: .24. 在平面直角坐标系中(如图),已知直线l:交x轴于点A , 交y轴于点B , 点C在x轴正半轴上,且 . 点D在线段上,且 , 过点C作的垂线,交的延长线于点E , 连接 .
(1)、求证:;(2)、求证: .24. 在平面直角坐标系中(如图),已知直线l:交x轴于点A , 交y轴于点B , 点C在x轴正半轴上,且 . 点D在线段上,且 , 过点C作的垂线,交的延长线于点E , 连接 .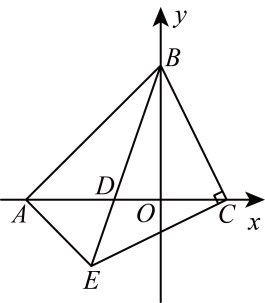 (1)、求点D的坐标;(2)、求证:;(3)、如果点P是直线上的动点,连接 , 当与相似时,求点P坐标.25. 在矩形中, , . 点P是射线上的动点,联结;
(1)、求点D的坐标;(2)、求证:;(3)、如果点P是直线上的动点,连接 , 当与相似时,求点P坐标.25. 在矩形中, , . 点P是射线上的动点,联结; (1)、如图1,当交于点E时,求的值;(2)、如图2,当点P在边上时(与端点B , C不重合),过点P作的垂线,交于点F , 交于点G . 设 , , 求y关于x的函数关系式,并写出自变量的取值范围.(3)、将沿直线翻折,点B落在点Q处,直线交边于点M , 当时,求的长.
(1)、如图1,当交于点E时,求的值;(2)、如图2,当点P在边上时(与端点B , C不重合),过点P作的垂线,交于点F , 交于点G . 设 , , 求y关于x的函数关系式,并写出自变量的取值范围.(3)、将沿直线翻折,点B落在点Q处,直线交边于点M , 当时,求的长.