上海市浦东新区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、单选题
-
1. 对于线段a,b,如果a∶b=2∶3,那么下列四个选项一定正确的是( )A、2a=3b B、b-a=1 C、 D、2. 中, , 若 , , 下列各式中正确的是A、 B、 C、 D、3. 已知 , , 而且和的方向相反,那么下列结论中正确的是( )A、 B、 C、 D、4. 如图,在边长为1个单位的方格纸中,它的顶点在小正方形顶点位置,其中点A、B、C、D也是小正方形的顶点,那么与相似的是( )
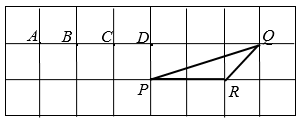 A、以点P、Q、A为顶点的三角形 B、以点P、Q、B为顶点的三角形 C、以点P、Q、C为顶点的三角形 D、以点P、Q、D为顶点的三角形5. 在△ABC中,中线AD、BE相交于点O,且S△BOD=5,则△ABC的面积是( )A、30 B、20 C、15 D、56. 如图,已知在中,边 , 高 , 正方形的顶点在边上,顶点分别在边和上,那么这个正方形的边长等于( )
A、以点P、Q、A为顶点的三角形 B、以点P、Q、B为顶点的三角形 C、以点P、Q、C为顶点的三角形 D、以点P、Q、D为顶点的三角形5. 在△ABC中,中线AD、BE相交于点O,且S△BOD=5,则△ABC的面积是( )A、30 B、20 C、15 D、56. 如图,已知在中,边 , 高 , 正方形的顶点在边上,顶点分别在边和上,那么这个正方形的边长等于( )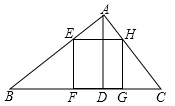 A、3 B、2.5 C、2 D、1.5
A、3 B、2.5 C、2 D、1.5二、填空题
-
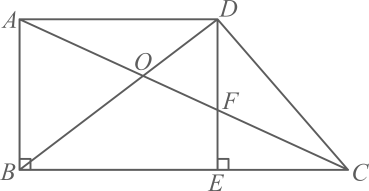
7. 已知、分别是的边、的延长线上的点,若 , 则的值是时,.8. 已知线段 , , 若线段是线段、的比例中项,则= .9. 已知,两个相似的与的最短边的长度之比是 , 若的周长是27,则的周长为 .10. 计算: .11. 若 , , 且 , 则与的位置关系是 .12. 如图,在中,D、E分别在边AB、AC上, , , , , 那么用、表示为: .
 13. 如图,在中,点是边的中点, , . 则= .
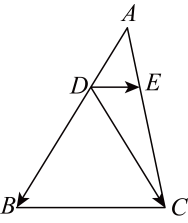
13. 如图,在中,点是边的中点, , . 则= .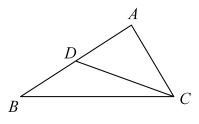 14. 如图,将沿射线方向平移得到 , 边与相交于点 , 如果 , 的面积等于 , 的面积等于 , 那么 .
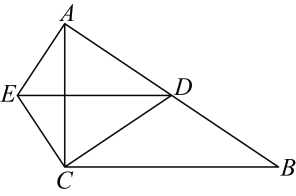
14. 如图,将沿射线方向平移得到 , 边与相交于点 , 如果 , 的面积等于 , 的面积等于 , 那么 .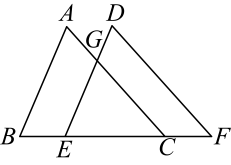 15. 如图,在 , 点、分别在、边上, , 若 , 则= .
15. 如图,在 , 点、分别在、边上, , 若 , 则= . 16. 如图,在边长相同的小正方形组成的网格中,点A、B、C都在这些小正方形的顶点上,则∠ABC的正切值是 .
16. 如图,在边长相同的小正方形组成的网格中,点A、B、C都在这些小正方形的顶点上,则∠ABC的正切值是 .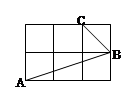 17. 如图,在△ABC中,AB=AC,∠A=36°, BD平分∠ABC交AC于点D,DE平分∠BDC交BC于点E,则= .
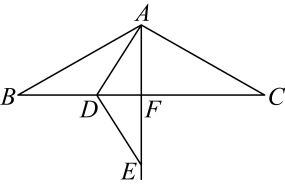
17. 如图,在△ABC中,AB=AC,∠A=36°, BD平分∠ABC交AC于点D,DE平分∠BDC交BC于点E,则= .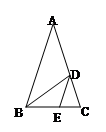 18. 在中, , 点D、E分别在上,且 , 若沿翻折,点C恰好落在边上,则的长为 .
18. 在中, , 点D、E分别在上,且 , 若沿翻折,点C恰好落在边上,则的长为 .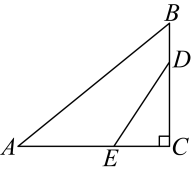
三、解答题
-
19. 计算
.
20. 如图,在△ABC中,矩形DEFG的一边DE在BC上,点G、F分别在AB、AC上,AH是BC边上的高,AH与GF相交于K,已知S△AGF:S△ABC=9:64,EF=10,求AH的长. 21. 如图,点E是平行四边形ABCD边BC上一点,且BE:EC=2:1,点F是边CD的中点,AE与BF交于点O.
21. 如图,点E是平行四边形ABCD边BC上一点,且BE:EC=2:1,点F是边CD的中点,AE与BF交于点O.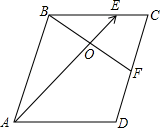 (1)、设= , = , 试用、表示;(2)、求BO:OF的值.22. 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)、设= , = , 试用、表示;(2)、求BO:OF的值.22. 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
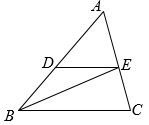 (1)、求证:AE•BC=BD•AC;(2)、如果 =3, =2,DE=6,求BC的长.
(1)、求证:AE•BC=BD•AC;(2)、如果 =3, =2,DE=6,求BC的长.