上海市松江区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、单选题
-
1. 已知(a、b、c、d都不为0),则下列各式一定成立的是( )A、 B、 C、 D、2. 已知在中,点、分别在边、上,那么下列条件中不能够判断的是( )A、 B、 C、 D、3. 已知是一个单位向量,、是非零向量,那么下列等式正确的是( )A、 B、 C、 D、4. 在中, , 如果AC=m , , 那么AB的长为( )A、 B、 C、 D、5. 下列说法正确的个数有( )
①所有正方形都相似; ②所有的矩形都相似; ③所有的菱形都相似;④所有的等腰三角形都相似.
A、1个 B、2个 C、3个 D、4个6. 如图,在 中,D、E分别在边AB、AC上, , 交AB于F , 那么下列比例式中正确的是 ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 在比例尺为的地图上,测得甲、乙两地的距离约为6厘米,那么甲、乙两地的实际距离约为千米.8. 如果 , 那么 .9. 如果两个相似三角形的对应高的比为 , 那么这两个三角形的面积比为 .10. 如图,已知平行四边形中,E是延长线上一点,交于点F , 且F为的黄金分割点(),那么的值为 .
 11. 在中, , , , 则的余切值为 .12. 如图,点G是的重心,交于点F , 若的面积为4,则的面积为 .
11. 在中, , , , 则的余切值为 .12. 如图,点G是的重心,交于点F , 若的面积为4,则的面积为 .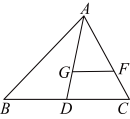 13. 如图,已知点M、N分别在的边、上, , 且 , 设 , 用表示 , 则 .
13. 如图,已知点M、N分别在的边、上, , 且 , 设 , 用表示 , 则 .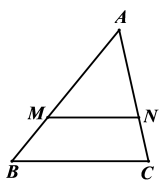 14. 已知为锐角, , 则= 度.15. 某人沿着一个斜坡往上走动了20米,他的垂直高度上升了10米,则这个坡的坡比为 .16. 已知菱形ABCD的边长为6,对角线AC与BD相交于点O , OE⊥AB , 垂足为点E , AC=4,那么sin∠AOE= .
14. 已知为锐角, , 则= 度.15. 某人沿着一个斜坡往上走动了20米,他的垂直高度上升了10米,则这个坡的坡比为 .16. 已知菱形ABCD的边长为6,对角线AC与BD相交于点O , OE⊥AB , 垂足为点E , AC=4,那么sin∠AOE= . 17. 如图,在中, , 的中垂线交于点D , 交于点E , 若 , , 则的正切值为 .
17. 如图,在中, , 的中垂线交于点D , 交于点E , 若 , , 则的正切值为 . 18. 如图,在中, , , 点在边上,且 , 将绕点旋转,使点的对应点落在的边上,则的长为 .
18. 如图,在中, , , 点在边上,且 , 将绕点旋转,使点的对应点落在的边上,则的长为 .
三、解答题
-
19. 计算: .20. 如图,已知梯形是一水库拦水坝的横断面示意图,坝顶宽米,坝高18米,迎水坡的坡度 , 背水坡的坡度 , 求坝底宽 .
 21. 如图,已知在中,是上的高,且 , , 矩形的顶点、在边上,顶点、分别在边、上.
21. 如图,已知在中,是上的高,且 , , 矩形的顶点、在边上,顶点、分别在边、上. (1)、设 , 矩形的周长为 , 求关于的函数解析式;(2)、当为正方形时,求EF的长度.22. 如图,已知在平行四边形中,对角线、交于点 , 点E在BC上,且 , 与交于点 .
(1)、设 , 矩形的周长为 , 求关于的函数解析式;(2)、当为正方形时,求EF的长度.22. 如图,已知在平行四边形中,对角线、交于点 , 点E在BC上,且 , 与交于点 . (1)、求的值;(2)、设 , , 试用 , 表示 .
(1)、求的值;(2)、设 , , 试用 , 表示 .




