上海市杨浦区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-13 类型:期中考试
一、单选题
-
1. 如果(、均不为零),那么下列四个结论中,正确的是( )A、 B、 C、 D、2. 在中, , , 那么下列结论正确的是( )A、 B、 C、 D、3. 下列两个三角形不一定相似的是( )A、有一个内角是的两个等腰三角形 B、有一个内角是的两个等腰三角形 C、有一个内角是的两个等腰三角形 D、有一个内角是的两个等腰三角形4. 下列说法中,正确的是( )A、如果和是相反向量,那么 B、如果和是平行向量,那么 C、如果 , 那么 D、如果(为非零向量),那么5. 已知点、分别在边、的延长线上,下列条件中一定能判断的是( )A、 B、 C、 D、6. 如图,在中,点、分别在边、上,四边形是平行四边形,点、在边上,交于点 . 甲、乙两位同学在研究这个图形时,分别产生了以下两个结论:①;② . 那么下列说法中,正确的是( )
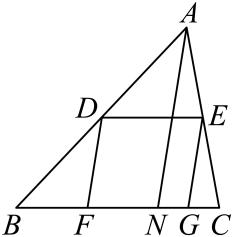 A、①正确②错误 B、①错误②正确 C、①、②皆正确 D、①、②皆错误
A、①正确②错误 B、①错误②正确 C、①、②皆正确 D、①、②皆错误二、填空题
-
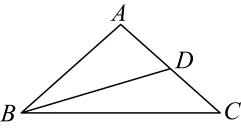
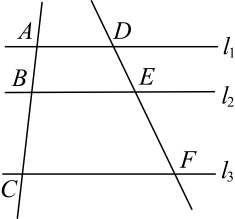
7. 已知 , 那么 .8. 已知点是线段的黄金分割点(),若 , 则9. 已知向量与单位向量方向相反,且 , 那么用向量的式子表示 .10. 如果两个相似三角形对应边之比是 , 且较小的三角形的周长是12,那么较大三角形的周长是 .11. 在中, , , , 那么 .12. 如图,已知 , , , , 那么 .
 13. 如图,是洞孔成像原理的示意图,物体平行物像 , 根据图中标注的尺寸,如果物体长 , 那么物像的长度是 .
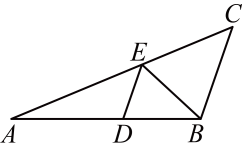
13. 如图,是洞孔成像原理的示意图,物体平行物像 , 根据图中标注的尺寸,如果物体长 , 那么物像的长度是 .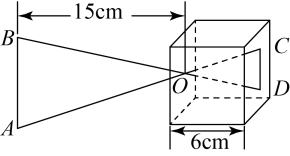 14. 已知点是的重心,过点作 , 分别交边、于点、 , 那么的值是 .15. 已知在与中, , , , 且 , 那么度.16. 如图,已知在中,点在边上, , , 那么的值是 .
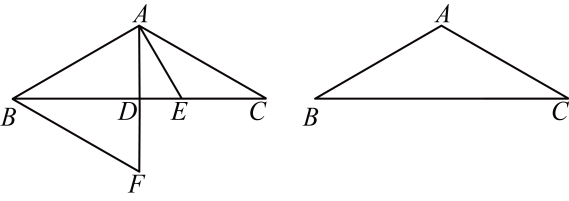
14. 已知点是的重心,过点作 , 分别交边、于点、 , 那么的值是 .15. 已知在与中, , , , 且 , 那么度.16. 如图,已知在中,点在边上, , , 那么的值是 . 17. 在中, , 点是边上的一点,线段将分成两个小三角形,如果这两个小三角形是相似三角形,且相似系数等于2,那么线段的长是 .18. 如图,已知在中, , , , 点是边上一点,将沿着翻折,点落在点处,连接 , 如果 , 设与边交于点 , 那么的值是 .
17. 在中, , 点是边上的一点,线段将分成两个小三角形,如果这两个小三角形是相似三角形,且相似系数等于2,那么线段的长是 .18. 如图,已知在中, , , , 点是边上一点,将沿着翻折,点落在点处,连接 , 如果 , 设与边交于点 , 那么的值是 .
三、解答题
-
19. 计算: .20. 如图,已知在平行四边形中,点是边的中点,和交于点 , 设 , .
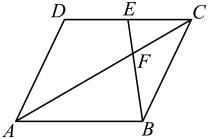 (1)、用向量、表示向量 , 即;(2)、在图中分别作出向量在、方向上的分向量(不要求写做法,但要指出所作图中表示结论的向量).21. 如图,在中,点是边上一点,分别交延长线、边于点、 , , 交于点 , , 求证: .
(1)、用向量、表示向量 , 即;(2)、在图中分别作出向量在、方向上的分向量(不要求写做法,但要指出所作图中表示结论的向量).21. 如图,在中,点是边上一点,分别交延长线、边于点、 , , 交于点 , , 求证: .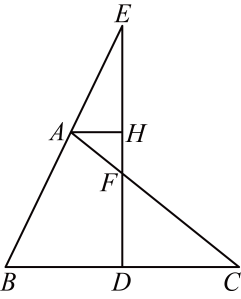 22. 如图,已知在中, , , 点是边的中点,连接 , 求的正弦值.
22. 如图,已知在中, , , 点是边的中点,连接 , 求的正弦值.