人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——期末测试卷
试卷更新日期:2023-12-13 类型:期末考试
一、选择题
-
1. 一元二次方程的一次项系数是( )A、 B、 C、 D、2. 如图,圆周角∠ACB =48°,则圆心角∠AOB的度数为( ).
 A、48° B、24° C、96° D、90°3. 年月是第个世界读书日,读书已经成为很多人的一种生活方式,城市书院是读书的重要场所之一,据统计,某书院对外开放的第一个月进书院人次,进书院人次逐月增加,到第三个月末累计进书院人次,若进书院人次的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、4. 在同一坐标系中,一次函数与二次函数的图象可能是( )A、
A、48° B、24° C、96° D、90°3. 年月是第个世界读书日,读书已经成为很多人的一种生活方式,城市书院是读书的重要场所之一,据统计,某书院对外开放的第一个月进书院人次,进书院人次逐月增加,到第三个月末累计进书院人次,若进书院人次的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、4. 在同一坐标系中,一次函数与二次函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,将△ABC绕点A旋转到△AB1C1 , 有下列说法:
5. 如图,将△ABC绕点A旋转到△AB1C1 , 有下列说法:
①AC=AB;②BC=B1C1;③∠BAC=∠B1AC1;④∠CAC1=∠BAB1 .
其中正确的有( ).
A、1个 B、2个 C、3个 D、4个6. 如图所示,抛物线的对称轴为直线 , 与轴的一个交点坐标为 , 其部分图象如图所示,有下列结论:①;②方程的两个根是;③;④当时,的取值范围是;⑤当时,随的增大而增大.其中正确的个数是( ). A、4 B、3 C、2 D、17. 船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔只要留心从船上到两个灯塔间的角度不超过一定的大小,就不用担心触礁如图所示的网格是正方形网格,点 , , , , , , 是网格线交点,当船航行到点的位置时,此时与两个灯塔 , 间的角度的大小一定无触礁危险那么,对于 , , , 四个位置,船处于____时,也一定无触礁危险( )
A、4 B、3 C、2 D、17. 船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔只要留心从船上到两个灯塔间的角度不超过一定的大小,就不用担心触礁如图所示的网格是正方形网格,点 , , , , , , 是网格线交点,当船航行到点的位置时,此时与两个灯塔 , 间的角度的大小一定无触礁危险那么,对于 , , , 四个位置,船处于____时,也一定无触礁危险( ) A、位置 B、位置 C、位置 D、位置8. 做好“垃圾分类”,倡导绿色健康的生活方式,是我们做为公民应尽的义务,如图所示垃圾分类标志,既是轴对称图形又是中心对称图形的是( )A、
A、位置 B、位置 C、位置 D、位置8. 做好“垃圾分类”,倡导绿色健康的生活方式,是我们做为公民应尽的义务,如图所示垃圾分类标志,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,AC,BC是两个半圆的直径,∠ACP=30°,AB=10 cm,则PQ的长为( ).
9. 如图,AC,BC是两个半圆的直径,∠ACP=30°,AB=10 cm,则PQ的长为( ). A、5cm B、cm C、6cm D、8cm10. 如图,在中,弦BC,ED所对的圆心角分别是 , 与互补,已知.当时,弦BC与DE之间的距离等于( ).
A、5cm B、cm C、6cm D、8cm10. 如图,在中,弦BC,ED所对的圆心角分别是 , 与互补,已知.当时,弦BC与DE之间的距离等于( ). A、7 B、1或7 C、 D、或
A、7 B、1或7 C、 D、或二、填空题
-
11. 口袋中装着若干个红球,6 个白球.从袋中任意摸一个球, 摸到红球的概率是 , 那么口袋中有红球个.12. 在△ABC中BC=2,AB=2 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,则AC边上的中线长为 .13. 如图甲所示,小敏利用课余时间制作了一个脸盆架,图乙是它的截面图,竖直放置的脸盆与脸盆架的交点为A,B.已知 , 脸盆的最低点到AB的距离为 , 则该脸盆的半径为.
 14. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为
14. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为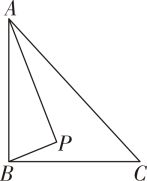 15. 如图所示,点C,D在上,直径 , 弦AC,BD相交于点.若 , 则阴影部分的面积为.
15. 如图所示,点C,D在上,直径 , 弦AC,BD相交于点.若 , 则阴影部分的面积为.
三、作图题
-
16. 如图,方格纸中的每个小方格都是边长为个单位长度的正方形,的顶点均在格点上,在建立平面直角坐标系后,点的坐标为 .
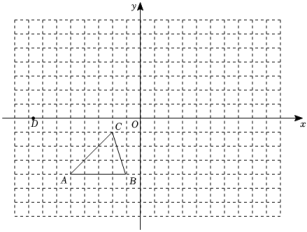 (1)、将向上平移个单位得到 , 画出;(2)、以为对称中心,画出关于该点对称的;(3)、经探究发现,和成中心对称,则对称中心坐标为;(4)、已知点为轴上不同于、的动点,当时, .
(1)、将向上平移个单位得到 , 画出;(2)、以为对称中心,画出关于该点对称的;(3)、经探究发现,和成中心对称,则对称中心坐标为;(4)、已知点为轴上不同于、的动点,当时, .四、解答题
-
17. 某商场购进一批品牌女装,购进时的单价是600元.根据市场调查,在一段时间内,销售单价是800元时,销售量是200件,销售单价每降低10元(销售单价是10的倍数),就可多售出20件.(1)、求销售量y(件)关于销售单价x(元)的函数表达式.(2)、求销售该品牌女装获得的利润W(元)关于销售单价x(元)的函数表达式.(3)、若服装厂要求该品牌女装的销售单价不低于760元且不高于800元,则商场销售这批女装获得的最大利润是多少?18. 小明和小亮两位同学做投掷骰子质地均匀的正方体试验,他们共做了次试验,试验的结果如下:
朝上的点数
出现的次数
(1)、 “点朝上”的频率为 ,“点朝上”的频率为 ;(2)、小明说:“根据试验,一次试验中出现点朝上的概率最大”他的说法正确吗?为什么?(3)、小明投掷一枚骰子,计算小明投掷点数不大于的概率.19. 如图,直线y=x+2与抛物线y=ax2 +bx +6(a≠0)相交于点A( , ),B(4,m),P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C. (1)、求抛物线的函数表达式.(2)、是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.(3)、求△PAC为直角三角形时点P的坐标.20. 如图所示,在△ABC中, , 点在BC边上,且 , 过 , C,三点的交AB于另一点 , 作直径AD,连结DE并延长交AB于点 , 连结CD,CF.
(1)、求抛物线的函数表达式.(2)、是否存在这样的点P,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.(3)、求△PAC为直角三角形时点P的坐标.20. 如图所示,在△ABC中, , 点在BC边上,且 , 过 , C,三点的交AB于另一点 , 作直径AD,连结DE并延长交AB于点 , 连结CD,CF. (1)、求证:四边形DCFG是平行四边形.(2)、当BE=4,CD=AB时,求的直径长.21. 已知直线与轴、轴分别交于A,D两点,抛物线经过点A,D,B是抛物线与轴的另一个交点.(1)、求这条抛物线的函数表达式及点的坐标.(2)、设是直线AD上一点,且 , 求点的坐标.(3)、如果在这条抛物线上,在轴的正半轴上是否存在点 , 使为等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由.
(1)、求证:四边形DCFG是平行四边形.(2)、当BE=4,CD=AB时,求的直径长.21. 已知直线与轴、轴分别交于A,D两点,抛物线经过点A,D,B是抛物线与轴的另一个交点.(1)、求这条抛物线的函数表达式及点的坐标.(2)、设是直线AD上一点,且 , 求点的坐标.(3)、如果在这条抛物线上,在轴的正半轴上是否存在点 , 使为等腰三角形?若存在,请求出点的坐标;若不存在,请说明理由.五、综合题
-
22. 若关于的一元二次方程有两个实数根,且其中一个根为另一个根的倍,则称这样的方程为“倍根方程”例如,一元二次方程的两个根是和 , 则方程就是“倍根方程”.(1)、若关于的一元二次方程是“倍根方程”,求的值;
(2)、若关于的一元二次方程是“倍根方程”,求该方程的根.23. 在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是D , E . (1)、如图1,当点D恰好落在边AB上时,旋转角α的度数是 ▲ ;(2)、如图2,当点B , D , E三点恰好在同一直线上时,判断此时直线CE与AB的位置关系,并说明理由;(3)、如图3,当B , D , E三点不在同一直线上时,连接BD , AE , 若△BCD的面积为cm2 , 求此时四边形ABDE的面积.
(1)、如图1,当点D恰好落在边AB上时,旋转角α的度数是 ▲ ;(2)、如图2,当点B , D , E三点恰好在同一直线上时,判断此时直线CE与AB的位置关系,并说明理由;(3)、如图3,当B , D , E三点不在同一直线上时,连接BD , AE , 若△BCD的面积为cm2 , 求此时四边形ABDE的面积.
-