人教版2023-2024年数学九年级第一学期期末扫芒清障复习卷——第二十四章综合测试
试卷更新日期:2023-12-13 类型:单元试卷
一、选择题
-
1. 如图、、是上的三点,是劣弧的中点, , 则的度数等于( )
 A、 B、 C、 D、2. 已知⊙O的半径是4cm,点P与⊙O在同一平面内,OP=3cm,下列结论正确的是( )A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、不能确定3. 下列命题中,正确的是( )A、和半径垂直的直线是圆的切线 B、平分直径一定垂直于弦 C、相等的圆心角所对的弧相等 D、垂直于弦的直径必平分弦所对的弧4. 如图,在⊙O中,直径AB⊥CD,若∠COB=65°,则∠BAD的度数是( )
A、 B、 C、 D、2. 已知⊙O的半径是4cm,点P与⊙O在同一平面内,OP=3cm,下列结论正确的是( )A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、不能确定3. 下列命题中,正确的是( )A、和半径垂直的直线是圆的切线 B、平分直径一定垂直于弦 C、相等的圆心角所对的弧相等 D、垂直于弦的直径必平分弦所对的弧4. 如图,在⊙O中,直径AB⊥CD,若∠COB=65°,则∠BAD的度数是( ) A、25° B、65° C、32.5° D、50°5. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 ( )
A、25° B、65° C、32.5° D、50°5. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 ( )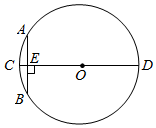 A、12寸 B、24寸 C、13寸 D、26寸6. 已知⊙O的半径为5cm,在圆心O的同侧有两条互相平行的弦,长度分别为6cm和8cm,则这两条平行弦之间的距离是( )A、1cm. B、2cm. C、3cm. D、4cm.7. 如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,连结BD,若∠B=32°,则∠C的大小为 ( )
A、12寸 B、24寸 C、13寸 D、26寸6. 已知⊙O的半径为5cm,在圆心O的同侧有两条互相平行的弦,长度分别为6cm和8cm,则这两条平行弦之间的距离是( )A、1cm. B、2cm. C、3cm. D、4cm.7. 如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,连结BD,若∠B=32°,则∠C的大小为 ( ) A、32° B、64° C、26° D、36°8. 如图,是的内接三角形,于点 , 若 , , 则( )
A、32° B、64° C、26° D、36°8. 如图,是的内接三角形,于点 , 若 , , 则( ) A、 B、 C、 D、9. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM和的长分别为( )
A、 B、 C、 D、9. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM和的长分别为( ) A、 , π B、 , π C、 , D、 , 2π10. 已知∠ADB,作图:
A、 , π B、 , π C、 , D、 , 2π10. 已知∠ADB,作图:
步骤1:以点D为圆心,适当长为半径作弧,分别交DA,DB于点M,N;再分别以点M,N为圆心,大于MN长为半径作弧,交于点E ,作射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径作半圆,分别交DA,DB,DE于点P,Q,C.
步骤3:连结PQ,OC.
有下列判断:
①= ;②OC∥DA ;③DP= PQ;④OC垂直平分PQ.
其中正确的有( ).
A、①③④ B、①②④ C、②③④ D、①②③④二、填空题
-
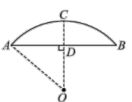
11. 兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m ,高度CD为 m.
 12. 如图,AB是⊙O的直径,若∠D=36°,则∠AOC=
12. 如图,AB是⊙O的直径,若∠D=36°,则∠AOC= 13. 下列说法不正确的是(只需填写序号).
13. 下列说法不正确的是(只需填写序号).①平分弧的直径垂直平分弧所对的弦;
②平分弦的直径平分弦所对的弧;
③垂直平分弦的直线必定经过圆心;
④平分弦的直径垂直于弦.
14. 如图,在⊙O中,直径MN⊥弦AB于点C.给出下列结论:
①AC=BC;②;③;④OC=CN;⑤∠AON=∠BON;⑥AM=BM.
其中正确的有(只需填写序号).
15. 如图,AB是⊙O的直径,C是⊙O上的一点,OD⊥BC于点D.若BC=3,AB=5,则OD的长为
三、综合题
-
16. 如图,在Rt中,为AC边上一点,连结OB.以OC为半径的半圆与AB边相切于点 , 交AC边于点.
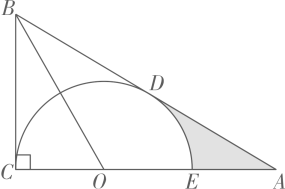 (1)、求证:.(2)、若.
(1)、求证:.(2)、若.①求半圆的半径.
②求图中阴影部分的面积.
17. 如图,是的直径,是的一条弦,连接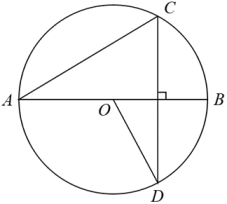 (1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.18. 如图, 是 的直径,点 是劣弧 中点, 与 相交于点 .连接 与 的延长线相交于点 .
(1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.18. 如图, 是 的直径,点 是劣弧 中点, 与 相交于点 .连接 与 的延长线相交于点 .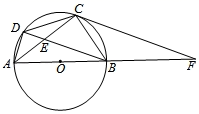 (1)、求证: 是 的切线;(2)、求证: ;(3)、若 ,求 的长.19. 如图,⊙O经过△ABC的顶点A,B,与边AC,BC分别交于点D,E,连接BD,AE,且∠ADB=∠CDE.
(1)、求证: 是 的切线;(2)、求证: ;(3)、若 ,求 的长.19. 如图,⊙O经过△ABC的顶点A,B,与边AC,BC分别交于点D,E,连接BD,AE,且∠ADB=∠CDE. (1)、求证:△ABE是等腰三角形;(2)、若AB=10,BE=12,求⊙O的半径r.20. 如图,线段与相切于点B , 交于点M , 其延长线交于点C , 连接 , , D为上一点且的中点为M , 连接 , .
(1)、求证:△ABE是等腰三角形;(2)、若AB=10,BE=12,求⊙O的半径r.20. 如图,线段与相切于点B , 交于点M , 其延长线交于点C , 连接 , , D为上一点且的中点为M , 连接 , . (1)、求的度数;(2)、四边形是否是菱形?如果是,请证明:如果不是,请说明理由;(3)、若 , 求的长.
(1)、求的度数;(2)、四边形是否是菱形?如果是,请证明:如果不是,请说明理由;(3)、若 , 求的长.


