人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——二十三章综合测试

试卷更新日期：2023-12-13 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列图形中属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以原点为中心，把点P(2，3)顺时针旋转90°，得到的点 P′的坐标为（）

A、(3， 2) B、(-3， 2) C、(2， -3) D、(-2， -3)

查看试题解析
3. 如图，把△ABC绕C点顺时针旋转35°，得到△A'B'C，A'B'交AC于点D，若∠A'DC=90°，则∠A的度数（）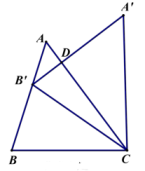

A、35° B、75° C、55° D、65°

查看试题解析
4. 如图，在△ABC中， ∠BAC=120°，将△ABC绕点C逆时针旋转得到△DEC，点A， B的对应点分别为D， E，连接AD. 当点A，D，E在同一条直线上时，下列结论一定正确的是（）

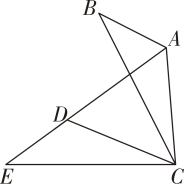A、∠ABC=∠ADC B、∠DAC=∠E C、AD=AC D、EA=BC

查看试题解析
5. 如图所示，在长方形ABCD中，AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置，H是EG的中点.若AB=6，BC=8，则线段CH的长为（）

A、2 $\sqrt{5}$ B、 $\sqrt{41}$ C、2 $\sqrt{10}$ D、 $\sqrt{21}$

查看试题解析
6. 边长为1的正方形 $O A B C$ 的顶点 $A$ 在 $x$ 正半轴上，点 $C$ 在 $y$ 正半轴上，将正方形 $O A B C$ 绕顶点 $O$ 顺时针旋转 $7 5^{°}$ ，如图所示，使点 $B$ 恰好落在函数 $y = a x^{2} (a < 0)$ 的图象上，则 $a$ 的值为（）

A、 $- \sqrt{2}$ B、 $- 1$ C、 $- \frac{3 \sqrt{2}}{4}$ D、 $- \frac{\sqrt{2}}{3}$

查看试题解析
7. 如图，已知 $▱ A B C D$ 中， $A E ⊥ B C$ 于点 $E$ ，以点 $B$ 为中心，取旋转角等于 $∠ A B C$ ，把 $△ B A E$ 顺时针旋转，得到 $△ B A' E'$ ，连接 $D A' .$ 若 $∠ A D C = 60 °$ ， $∠ A D A' = 50 °$ ，则 $∠ D A' E'$ 的大小为（）

A、 $130 °$ B、 $150 °$ C、 $160 °$ D、 $170 °$

查看试题解析
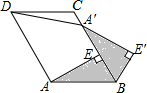8. 下列说法中，正确的有（）.
①图形旋转时，图形上的每一个点都绕旋转中心旋转了相同的角度；
②图形旋转时，对应点与旋转中心的距离相等；
③图形旋转时，对应线段相等，对应角相等，图形的形状和大小不变；
④两个图形成中心对称，可看作是一个图形绕着对称中心旋转180°得到另一个图形.

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在平面直角坐标系中，菱形 $O A B C$ 的边长为 $2 \sqrt{6}$ ，点 $B$ 在 $x$ 轴的正半轴上，且 $∠ A O C = 60 °$ ，将菱形 $O A B C$ 绕原点 $O$ 逆时针方向旋转 $60 °$ ，得到四边形 $O A' B' C' ($ 点 $A'$ 与点 $C$ 重合 $)$ ，则点 $B'$ 的坐标是（）

A、 $(3 \sqrt{6} ， 3 \sqrt{2})$ B、 $(3 \sqrt{2} ， 3 \sqrt{6})$ C、 $(3 \sqrt{2} ， 6 \sqrt{2})$ D、 $(6 \sqrt{2} ， 3 \sqrt{6})$

查看试题解析
10. 如图，将边长为 $\sqrt{3}$ 的正方形 $A B C D$ 绕点 $B$ 逆时针旋转 $30 °$ 得到正方形 $A' B C' D'$ ， $A D$ 与 $C' D'$ 交于点 $M$ ，那么图中点 $M$ 的坐标为（）

A、 $(\sqrt{3} ， 1)$ B、 $(1 ， \sqrt{3})$ C、 $(\sqrt{3} ， \frac{\sqrt{3}}{2})$ D、 $(\frac{\sqrt{3}}{2} ， \sqrt{3})$

查看试题解析

二、填空题

11. 如图，点O为等边 $△ A B C$ 内一点， $A O = 8$ ， $B O = 6$ ， $C O = 10$ ，将 $△ A O C$ 绕点A顺时针方向旋转60°，使AC与AB重合，点O旋转至点 $O_{1}$ 处，连接 $O O_{1}$ ，则 $△ A O B$ 的面积是．

查看试题解析
12. 如图， $P$ 为正方形 $A B C D$ 内一点，且 $B P = 2$ ， $P C = 3$ ， $∠ A P B = 135 °$ ，将 $△ A P B$ 绕点 $B$ 顺时针旋转 $90 °$ 得到 $△ C P' B$ ，连接 $P P'$ ，则 $A P =$ ．

查看试题解析
13. 如图，将腰长为3的等腰直角三角形ABC绕点A逆时针旋转15°得到△AB'C'，则图中阴影部分的面积为

查看试题解析
14. 如图，将△AOB绕点O逆时针方向旋转45°后得到△COD．若∠AOB=15° ，则∠AOD的度数是

查看试题解析
15. 如图所示，将Rt $△ A B C$ 的斜边AB绕点 $A$ 按顺时针方向旋转 $α (0^{°} < α <$ $9 0^{°})$ 得到AE，直角边AC绕点 $A$ 按逆时针方向旋转 $β (0^{°} < β < 9 0^{°})$ 得到AF，连结EF.若 $A B = 3 ， A C = 2$ ，且 $α + β = ∠ B$ ，则 $E F =$ .

查看试题解析

三、作图题

16. 如图，在直角坐标系中，已知△ABC的三个顶点坐标分别是A(1，1)，B(4，1) ，C(3，3)．
⑴将△ABC向下平移5个单位后得到△A₁B₁C₁ ，画出△A₁B₁C₁ ．
⑵将△ABC绕原点O逆时针旋转90°后得到△A₂B₂C₂ ，画出△A₂B₂C₂ ．
⑶判断以O，A₁ ， B为顶点的三角形的形状．(无需说明理由)

查看试题解析
17. 如图，在正方形网格中，建立平面直角坐标系， $△ A B C$ 的三个顶点都在格点上，点 $A (1 ， 1)$ ， $B (2 ， 4)$ .

（1）将 $△ A B C$ 绕着点 $O$ 逆时针旋转90°，画出旋转后的 $△ A_{1} B_{1} C_{1}$ ；
（2）画出 $△ A B C$ 关于原点对称的 $△ A_{2} B_{2} C_{2}$ ；
（3）在 $x$ 轴上找一点 $D$ ，使 $A_{1} D + B_{1} D$ 的值最小，请直接写出点 $D$ 的坐标.

查看试题解析
18. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，O、M也在格点上．

(1)、画出△ABC关于直线OM对称的△A₁B₁C₁；

(2)、画出△ABC绕点O按顺时针方向旋转90°后所得的△A₂B₂C₂；

(3)、△A₁B₁C₁与△A₂B₂C₂组成的图形是轴对称图形吗？如果是轴对称图形，请画出对称轴．

查看试题解析

四、综合题

19. 如图，将△ABC绕点A顺时针旋转得到△AED，并使C点的对应点D点落在直线BC上，

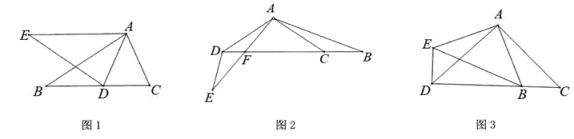(1)、如图1，证明：DA平分∠EDC；

(2)、如图2，AE与BD交于点F，若∠AFB＝50°，∠B＝20°，求∠BAC的度数；

(3)、如图3，连接BE，若EB＝13，ED＝5，CD＝17，则AD的长为．

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (2 ， 4)$ ， $B (1 ， 1)$ ， $C (4 ， 3)$ ．
⑴请画出 $△ A B C$ 关于原点对称的 $△ A_{1} B_{1} C_{1}$ ；
⑵请画出 $△ A B C$ 绕点B逆时针旋转 $90 °$ 后的 $△ A_{2} B_{2} C_{2}$ ，求点A到 $A_{2}$ 所经过的路径长．

查看试题解析
21. 已知，如图1，四边形 $A B C D$ 是正方形，E，F分别在边 $B C$ 、 $C D$ 上，且 $∠ E A F = 45 °$ ，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法．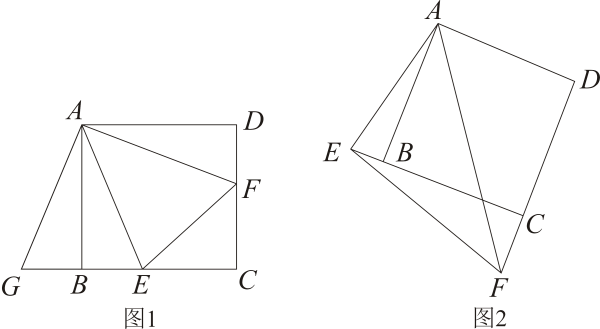

(1)、在图1中，连接 $E F$ ，为了证明结论“ $E F = B E + D F$ ”，小亮将 $Δ A D F$ 绕点A顺时针旋转 $90 °$ 后解答了这个问题，请按小亮的思路写出证明过程；

(2)、如图2，当 $∠ E A F$ 绕点A旋转到图2位置时，试探究 $E F$ 与 $D F$ 、 $B E$ 之间有怎样的数量关系？

查看试题解析
22. 已知在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， $D$ 为直线 $B C$ 上的一动点（点 $D$ 不与点 $B ， C$ 重合），将 $A D$ 绕点 $A$ 逆时针旋转 $90 °$ 得到 $A E$ ，连接 $C E ， D E$ ．

(1)、如图①，当点 $D$ 在边 $B C$ 上时，求证： $B C = C D + C E$ ；

(2)、当点 $D$ 在直线 $B C$ 上时，如图②、图③所示，线段 $B C ， C D ， C E$ 之间又有怎样的数量关系？请直接写出你的猜想，不需证明．

查看试题解析
23. 在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E.

(1)、当点E恰好在AC上时，如图1，求∠ADE的大小；

(2)、若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形.

查看试题解析