人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——二十二章综合测试

试卷更新日期：2023-12-13 类型：单元试卷

进入出卷网下载

一、选择题

1. 平面直角坐标系中，将抛物线 $y = - 2 x^{2}$ 先向左平移2个单位，再向下平移1个单位，得到的抛物线的表达式是（）

A、 $y = - 2 (x + 2)^{2} + 1$ B、 $y = - 2 (x + 2)^{2} - 1$ C、 $y = - 2 (x - 2)^{2} + 1$ D、 $y = - 2 (x - 2)^{2} - 1$

查看试题解析
2. 如图，下列选项中，能描述函数y＝ax²与y＝ax+a的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
3. 已知抛物线 $y = - x^{2} + 2 x + c$ 过点 $(0 ， y_{1})$ ， $(1 ， y_{2})$ ， $(3 ， y_{3})$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{3} > y_{1} > y_{2}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{3} > y_{2} > y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
4. 关于二次函数y= (x-2)²+3的最大值或最小值，下列叙述正确的是（）

A、当x=2时，y有最大值3 B、当x=-2时，y有最大值3 C、当x=2时，y有最小值3 D、当x=-2时，y有最小值3

查看试题解析
5. 2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌，比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线 $y = - \frac{1}{4} x^{2} + \frac{3}{4} x + 1$ 图象的一部分，其中出球点 $B$ 离地面 $O$ 点的距离是1米，则球落地点 $A$ 到 $O$ 点的距离是（）．

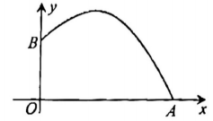A、1米 B、3米 C、4米 D、 $\frac{25}{16}$ 米

查看试题解析
6. 如图，等边 $△ A B C$ 的边长为4，直线l经过点A且直线 $l ⊥ A C$ ，直线l从点A出发沿A-C以1cm/s的速度向点C移动，直到经过点C即停止，直线l分别与AB或BC交于点M ，与AC交于点N ，若 $△ A M N$ 的面积为y（cm $^{2}$ ），直线l的移动时间为x（s），则下面最能反映y与x之间函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
7. 已知抛物线 $y = a x^{2} + b x + c (a > 0)$ ，且 $a + b + c = - \frac{1}{2}$ ， $a - b + c = - \frac{3}{2}$ ，下列结论：① $a b c < 0$ ， ② $3 a + 2 b + c > 0$ ， ③抛物线与 $x$ 轴正半轴必有一个交点，④当 $2 \leq x \leq 3$ 时， $y$ 最小 $= 3 a$ ， ⑤抛物线与直线 $y = x - c$ ，有一个交点，其中正确结论的个数有（）

A、2 B、3 C、4 D、5

查看试题解析
8. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，给出下列结论：①b²-4ac＞0；②2a+b＜0；③4a-2b+c＝0；④a+b+c＞0．其中正确的是（）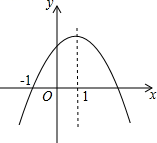

A、①② B、②③ C、③④ D、①④

查看试题解析
9. 若 $y = (m - 2) x^{m^{2} - 2} - x + 1$ 是二次函数，则m的值是（）

A、4 B、2 C、-2 D、-2或2

查看试题解析
10. 二次函数y＝ax²-2ax+c（a≠0）的图象过点（3，0），方程ax²-2ax+c＝0的解为（）

A、x₁＝-3，x₂＝-1 B、x₁＝-1，x₂＝3 C、x₁＝1，x₂＝3 D、x₁＝-3，x₂＝1

查看试题解析

二、填空题

11. 张师傅去华开了一家超市，今年2月份开始盈利，3月份盈利5000元，5月份盈利达到7200元，从3月到5月，设每月盈利的平均增长率都是x．则根据题意。可列方程：

查看试题解析
12. 若二次函数 $y = (2 a - 6) x^{2} + 4$ 的图象开口向下，则 $a$ 的取值范围是．

查看试题解析
13. 飞机着陆后滑行的距离y（单位： m）关于滑行时间t：（单位： s）的函数解析式是 $y = 60 t - \frac{6}{5} t^{2}$ ，从飞机着陆至停下来共滑行米.

查看试题解析
14. 如图，抛物线 $y = x^{2} + x$ 交 $x$ 轴的负半轴于点 $A$ ，点 $B$ 是 $y$ 轴的正半轴上一点，点 $A$ 关于点 $B$ 的对称点 $A^{'}$ 恰好落在抛物线上．过点 $A^{'}$ 作 $x$ 轴的平行线交抛物线于另一点 $C$ ，则点 $C$ 的坐标为．

查看试题解析
15. 如图，已知二次函数y＝ax²+bx+c的图象过点（3，0），对称轴为直线x＝1，则下列结论：①abc＜0；②ax²+bx+c＝0的两个根是x₁＝-1，x₂＝3；③当x＜1时，y随着x的增大而增大；④4a+2b+c＜0．（填写序号）．

查看试题解析

三、解答题

16. 如图，一条隧道的横截面是由一段抛物线及矩形的三边围成的，隧道宽BC=10米，矩形部分高AB=3米，抛物线的最高点E离地面OE=6米．按如图建立以BC所在直线为x轴，OE所在直线为y轴的直角坐标系．

(1)、求抛物线的函数表达式．

(2)、该隧道内设双车道，现有一辆货运卡车高4.5米、宽3米，这辆货运卡车能顺利通过隧道吗？请说明理由．

查看试题解析
17. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行，大熊猫是成都最具特色的对外传播标识物和“品牌图腾”，是天府之国享有极高知名度的个性名片．此次成都大运会吉祥物“蓉宝”（如图1）便是以熊猫基地真实的大熊猫“芝麻”为原型创作的．某商店销售“蓉宝”的公仔毛绒玩具，进价为30元/件，经市场调查发现：该商品的月销售量y（件）与销售价x（元/件）之间的关系如图2所示．
图1 图2

(1)、求y关于x的函数解析式；

(2)、由于某种原因，该商品进价提高了a元/件（ $a > 0$ ），如果规定该玩具售价不超过40元/件，该商品在今后的销售中，月销售量与销售价仍然满足（1）中的函数关系，若该商品的月销售最大利润是2400元，求a的值．

查看试题解析
18. 某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销，经过市场调查，得出每天销售量y（件）是每件售价x（元）（x为正整数）的一次函数，其部分对应数据如下表所示：
每件售价x（元）
…
15
16
17
18
…
每天销售量y（件）
…
150
140
130
120
…

(1)、求y关于x的函数解析式；

(2)、若用w（元）表示工艺品厂试销该工艺品每天获得的利润，试求w关于x的函数解析式；

(3)、该工艺品每件售价为多少元时，工艺品厂试销该工艺品每天获得的利润最大，最大利润是多少元？

查看试题解析
19. 如图，直线y= $- \frac{4}{3}$ x+4与x轴，y轴分别交于点A，B．抛物线L：y=-x²+bx+3c经过点A，L与线段AB的另一个交点为点C（不与点B重合），P（m，n）为抛物线上点A、C之间的一动点

(1)、点A的坐标为，点B的坐标为

(2)、求b，c的数量关系：

(3)、若L经过OB的中点，
①求L的解析式：
②求点P到AB距离的最大值．

查看试题解析
20. 在平面直角坐标系中，抛物线p=-x²+bx+c （b、c为常数）与x轴交点的坐标是（3，0），对称轴为直线x=1．

(1)、求此抛物线所对应的二次函数的表达式，

(2)、直接写出当x≥2，函数值y随x的增大而增大时y的取值范围，

(3)、点A、点B均在这个抛物线上，点A的横坐标为a，点B的横坐标为4+a，将A、B两点之间的部分（包括A、B两点）记为图象G．
①当A、B两点纵坐标相等时，求AB中点的坐标。
②设图象G的最高点的纵坐标与最低点的纵坐标的差为h，求h与a的函数关系式，并写出a的取值范围．

查看试题解析
21. 如图，直线 $y = x - 3$ 与抛物线 $y = - x^{2} + b x + c$ 相交于 $A ， B$ 两点，与抛物线的对称轴交于点 $M$ ，且点 $A ， B$ 分別在 $x$ 轴， $y$ 轴上，抛物线的顶点为 $C$ ．

(1)、求抛物线的解析式和点 $M$ 的坐标；

(2)、点 $N$ 是线段 $C M$ 上的动点， $N P ⊥ C M$ 交 $B ， C$ 两点之间的抛物线于点 $P$ ，点 $P$ 的坐标为 $P (x ， n) ， m = M P^{2}$ ．
①求 $N P^{2}$ （用含 $n$ 的代数式表示）；
②求 $m$ 与 $n$ 之间的函数关系式，并求出 $m$ 的最小值．

查看试题解析
22. 如图，在平面直角坐标系中，直线y=x+b与x轴交于点A（4，0），与y轴交于点B，过，A、B两点的抛物线交x轴于另一点C，且OA=2OC，点F是直线AB下方抛物线上的一个动点，连接FA、FB．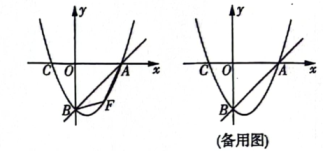

(1)、求抛物线的解析式；

(2)、当点F与抛物线的顶点重合时，△ABF的面积为；

(3)、求四边形FAOB面积的最大值及此时点F的坐标；

(4)、在（3）的条件下，点Q为平面内y轴右侧的一点，是否存在点Q及平面内另一点M，使得以A、F、Q、M为顶点的四边形是正方形？若存在，直接写出点Q的坐标；若不存在，说明理由．

查看试题解析
23. 如图，抛物线y＝ax²+bx﹣6与x轴相交于A ， B两点，与y轴相交于点C ， OA＝2，OB＝4，直线l是抛物线的对称轴，在直线l右侧的抛物线上有一动点D ，连接AD ， BD ， BC ， CD ．

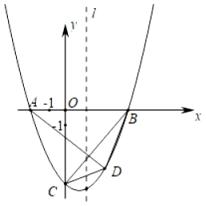(1)、求抛物线的函数表达式；

(2)、若点D在x轴的下方，当△BCD的面积是 $\frac{9}{2}$ 时，求△ABD的面积；

(3)、在（2）的条件下，点M是x轴上一点，点N是抛物线上一动点，是否存在点N ，使得以点B ， D ， M ， N为顶点，以BD为一边的四边形是平行四边形，若存在，求出点N的坐标；若不存在，请说明理由．

查看试题解析

每件售价x（元）	…	15	16	17	18	…
每天销售量y（件）	…	150	140	130	120	…