人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——24.4弧长及扇形面积
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 已知在半径为R的圆中,长为l的弧所对的圆心角度数为n°,则下列关系不正确的是( )A、l= B、n= C、R= D、l=2nR2. 如图,点A,B,C是⊙O上的点,且∠ACB=40°,阴影部分的面积为2π,则此扇形的半径为( ).
 A、2 B、3 C、4 D、53. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB的长为30cm,贴纸部分BD的长为20cm,则贴纸部分的面积是( )
A、2 B、3 C、4 D、53. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB的长为30cm,贴纸部分BD的长为20cm,则贴纸部分的面积是( ) A、100πcm2 B、πcm2 C、πcm2 D、800πcm24. 如图,长方形的宽为a , 长为b , 若单项式与是同类项,两个圆的圆心均为长方形的顶点,则图中阴影部分的面积为( )
A、100πcm2 B、πcm2 C、πcm2 D、800πcm24. 如图,长方形的宽为a , 长为b , 若单项式与是同类项,两个圆的圆心均为长方形的顶点,则图中阴影部分的面积为( ) A、 B、 C、 D、5. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,且B,E是半圆弧的三等分点.若的长为 , 则图中阴影部分的面积为( ).
A、 B、 C、 D、5. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E,且B,E是半圆弧的三等分点.若的长为 , 则图中阴影部分的面积为( ). A、 B、 C、 D、6. 如图,以AB为直径,点O为圆心的半圆经过点C.若AC=BC=2,则图中阴影部分的面积是( ).
A、 B、 C、 D、6. 如图,以AB为直径,点O为圆心的半圆经过点C.若AC=BC=2,则图中阴影部分的面积是( ). A、 B、 C、 D、7. 如图所示,AB是的直径,将弦AC绕点按顺时针方向旋转得到AD,此时点的对应点落在AB上,延长CD,交于点 , 若 , 则图中阴影部分的面积为( ).
A、 B、 C、 D、7. 如图所示,AB是的直径,将弦AC绕点按顺时针方向旋转得到AD,此时点的对应点落在AB上,延长CD,交于点 , 若 , 则图中阴影部分的面积为( ). A、 B、 C、 D、8. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图所示,已知矩形的宽为 , 高为 , 则改建后门洞的圆弧长是( ).
A、 B、 C、 D、8. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图所示,已知矩形的宽为 , 高为 , 则改建后门洞的圆弧长是( ). A、 B、 C、 D、9. 已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A、 B、 C、 D、9. 已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( ) A、π B、3π C、π D、π10. 如图,四边形是的内接正方形,直线且平分 , 交于点 , 若 , 则阴影部分面积为( )
A、π B、3π C、π D、π10. 如图,四边形是的内接正方形,直线且平分 , 交于点 , 若 , 则阴影部分面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,点C、D是⊙O上直径AB两侧的两点,若∠ACD= 60°.AB=8.则的长为 (结果保留π).
 12. 如图所示,扇形AOB中,∠AOB=140°,点C为OA中点,OA=8,CD⊥AO交于D , 以OC为半径画交OB于E , 则图中阴影部分面积为 .
12. 如图所示,扇形AOB中,∠AOB=140°,点C为OA中点,OA=8,CD⊥AO交于D , 以OC为半径画交OB于E , 则图中阴影部分面积为 . 13. 如图,在△ABC中,∠ACB=90°,∠A=60°,以点A为圆心,AC长为半径画弧,交边AB于点D,以点B为圆心,BD长为半径画圆弧,交边BC于点E,若AC=2,则图中阴影部分图形的面积和为(结果保留π).
13. 如图,在△ABC中,∠ACB=90°,∠A=60°,以点A为圆心,AC长为半径画弧,交边AB于点D,以点B为圆心,BD长为半径画圆弧,交边BC于点E,若AC=2,则图中阴影部分图形的面积和为(结果保留π). 14. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一如图, , 分别与相切于点 , , 延长 , 交于点若 , 的半径为 , 则图中的长为 结果保留
14. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一如图, , 分别与相切于点 , , 延长 , 交于点若 , 的半径为 , 则图中的长为 结果保留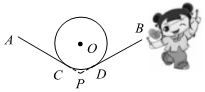 15. 如图,为半圆内一点,为圆心,直径长为 , , , 将绕圆心逆时针旋转至 , 点在上,则边扫过区域图中阴影部分的面积为结果保留
15. 如图,为半圆内一点,为圆心,直径长为 , , , 将绕圆心逆时针旋转至 , 点在上,则边扫过区域图中阴影部分的面积为结果保留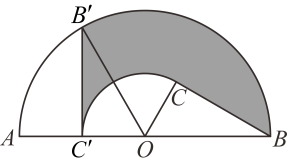
三、解答题
-
16. 已知:如图,A,B,C是⊙O上的三点,且=2 . 过点B作BD⊥OC于点D.
 (1)、求证:AB=2BD.(2)、若AB= , CD=1,求图中阴影部分的面积.17. 如图,以为直径的经过的中点 , 于点 .
(1)、求证:AB=2BD.(2)、若AB= , CD=1,求图中阴影部分的面积.17. 如图,以为直径的经过的中点 , 于点 . (1)、求证:是的切线;(2)、当 , 时,求图中阴影部分的面积结果保留根号和 .18. 如图,在中, , 平分 , 交于点 , 点在上,经过、两点,交于点 , 交于点 .
(1)、求证:是的切线;(2)、当 , 时,求图中阴影部分的面积结果保留根号和 .18. 如图,在中, , 平分 , 交于点 , 点在上,经过、两点,交于点 , 交于点 .
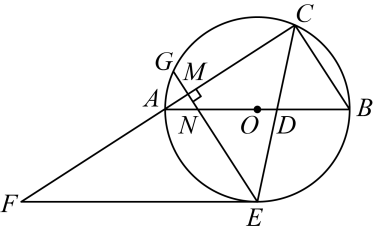
 (1)、求证:是的切线;(2)、若的半径是 , 是的中点,求阴影部分的面积结果保留和根号19. 如图,内接于 , 交于点 , 交于点 , 交于点 , 连接 , .
(1)、求证:是的切线;(2)、若的半径是 , 是的中点,求阴影部分的面积结果保留和根号19. 如图,内接于 , 交于点 , 交于点 , 交于点 , 连接 , .
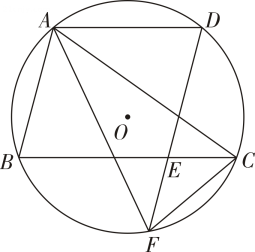 (1)、求证:;
(1)、求证:;
(2)、若的半径为 , , 求的长结果保留 .20. 将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,求图中阴影部分的面积.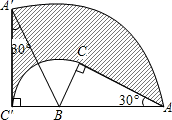 21. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,求该圆锥的母线长 .
21. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,求该圆锥的母线长 .
四、综合题