人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——24.3正多边形和圆
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( ).
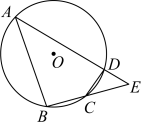
 A、45° B、50° C、60° D、75°2. 如图,延长圆内接四边形ABCD的边AB,DC,相交于点E,延长边AD,BC,相交于点F.若∠E=30°,∠F=50° ,则∠A的度数为( ).
A、45° B、50° C、60° D、75°2. 如图,延长圆内接四边形ABCD的边AB,DC,相交于点E,延长边AD,BC,相交于点F.若∠E=30°,∠F=50° ,则∠A的度数为( ). A、20° B、30° C、50° D、60°3. 如图所示,正六边形ABCDE的边长为6,以顶点为圆心、AB的长为半径画圆,则图中阴影部分的面积为( ).
A、20° B、30° C、50° D、60°3. 如图所示,正六边形ABCDE的边长为6,以顶点为圆心、AB的长为半径画圆,则图中阴影部分的面积为( ). A、 B、 C、 D、4. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )
A、 B、 C、 D、4. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )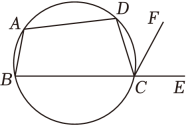 A、30° B、48° C、54° D、60°5. 如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )
A、30° B、48° C、54° D、60°5. 如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( ) A、100°. B、105°. C、110°. D、120°.6. 我们都知道蜂巢是很多个正六边形组合来的正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固、如图,某蜂巢的房孔是边长为的正六边形 , 若的内接正六边形为正六边形 , 则的长为( )
A、100°. B、105°. C、110°. D、120°.6. 我们都知道蜂巢是很多个正六边形组合来的正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固、如图,某蜂巢的房孔是边长为的正六边形 , 若的内接正六边形为正六边形 , 则的长为( ) A、 B、 C、 D、7. 如图,是的直径,内接于 , 延长在外相交于点 , 若 , 则的度数是( )
A、 B、 C、 D、7. 如图,是的直径,内接于 , 延长在外相交于点 , 若 , 则的度数是( )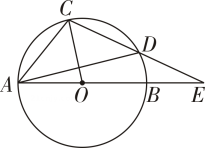 A、 B、 C、 D、8. 如图,△ABC内接于⊙O,D,E为圆上的点,连结AD,BD,AE,CE.若∠BAC=50°,则∠D与∠E的和为( )
A、 B、 C、 D、8. 如图,△ABC内接于⊙O,D,E为圆上的点,连结AD,BD,AE,CE.若∠BAC=50°,则∠D与∠E的和为( )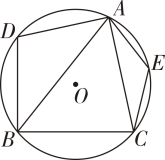 A、220° B、230° C、240° D、250°9. 如图所示,四边形ABCD是的内接四边形,BE是的直径,连结AE.若 , 则的度数是( ).
A、220° B、230° C、240° D、250°9. 如图所示,四边形ABCD是的内接四边形,BE是的直径,连结AE.若 , 则的度数是( ). A、 B、 C、 D、10. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).
A、 B、 C、 D、10. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).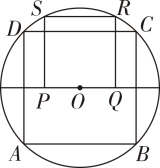 A、1 :2 B、1:3 C、2:3 D、2:5
A、1 :2 B、1:3 C、2:3 D、2:5二、填空题
-
11. 如图,四边形是的内接四边形,平分 , 连结 , , , 若等于 , 则的度数为 .
 12. 如图,过A、C、D三点的圆的圆心为点E , 过B、F、E三点的圆的圆心为D , 如果∠A=66°,那么∠θ= .
12. 如图,过A、C、D三点的圆的圆心为点E , 过B、F、E三点的圆的圆心为D , 如果∠A=66°,那么∠θ= . 13. 如图,在中,是的中点,作点关于弦的对称点 , 连接并延长交于点 , 过点作于点 , 若 , 则等于度.
13. 如图,在中,是的中点,作点关于弦的对称点 , 连接并延长交于点 , 过点作于点 , 若 , 则等于度. 14. 如图,A,B,C三点都在⊙O上,已知∠AOC=138°,则∠OAB+∠OCB=°.
14. 如图,A,B,C三点都在⊙O上,已知∠AOC=138°,则∠OAB+∠OCB=°. 15. 如图,四边形ABCD内接于 , BC为的直径,.若 , 则的度数为°.
15. 如图,四边形ABCD内接于 , BC为的直径,.若 , 则的度数为°.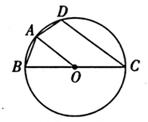
三、解答题
-
16. 如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
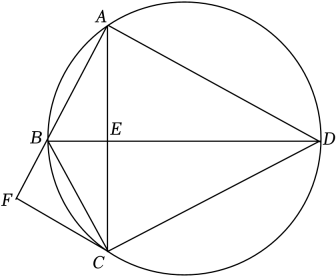 (1)、求证DB平分∠ADC , 并求∠BAD的大小;(2)、过点C作CF∥AD交AB的延长线于点F , 若AC=AD , BF=2求此圆半径的长17. 如图,⊙C经过原点O,且与两坐标轴分别交于点A(0,3)和点B.M是劣弧OB上一点,∠BMO=120°.求⊙C的半径长.
(1)、求证DB平分∠ADC , 并求∠BAD的大小;(2)、过点C作CF∥AD交AB的延长线于点F , 若AC=AD , BF=2求此圆半径的长17. 如图,⊙C经过原点O,且与两坐标轴分别交于点A(0,3)和点B.M是劣弧OB上一点,∠BMO=120°.求⊙C的半径长.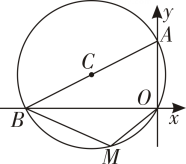 18. 如图所示,四边形ABCD内接于为的直径,.
18. 如图所示,四边形ABCD内接于为的直径,. (1)、试判断的形状,并给出证明.(2)、若 , 求CD的长度.19. 如图,⊙ 是△ 的外接圆, 为直径,弦 , 交 的延长线于点 ,求证:
(1)、试判断的形状,并给出证明.(2)、若 , 求CD的长度.19. 如图,⊙ 是△ 的外接圆, 为直径,弦 , 交 的延长线于点 ,求证: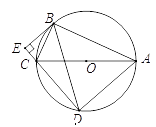
(Ⅰ) ;
(Ⅱ) 是⊙ 的切线.
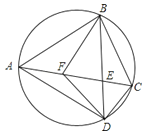
20. 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;
(2)求证:CD⊥DF.
四、综合题