人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——24.2点和圆、直线和园的位置关系
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 已知的半径为 , , 则点和的位置关系是( )A、点在圆上 B、点在圆外 C、点在圆内 D、不确定2. 平面内,⊙O的半径为3,若点P在⊙O外,则OP的长可能为( )A、4 B、3 C、2 D、13. 已知⊙O的半径为3cm,P为圆外一点,则OP的长可能是( ).A、1cm B、2cm C、3cm D、4cm4. 如图,、、是的切线,切点分别是、、若 , , 则的长是( )
 A、 B、 C、 D、5. 如图,PA、PC是⊙O的两条切线,点A、C为切点,点B为⊙O上任意一点,连接AB、BC , 若∠B=52°,则∠P的度数为( ).
A、 B、 C、 D、5. 如图,PA、PC是⊙O的两条切线,点A、C为切点,点B为⊙O上任意一点,连接AB、BC , 若∠B=52°,则∠P的度数为( ).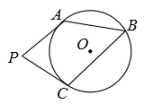 A、68° B、104° C、70° D、76°6. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为5km的雷达,监测点的分布情况如图,如果将雷达装置设在P点,每一个小格的边长为1km , 那么能被雷达监测到的最远点为( )
A、68° B、104° C、70° D、76°6. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为5km的雷达,监测点的分布情况如图,如果将雷达装置设在P点,每一个小格的边长为1km , 那么能被雷达监测到的最远点为( )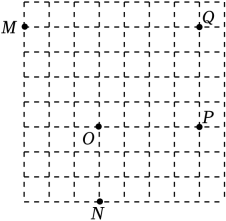 A、M点 B、N点 C、P点 D、Q点7. 下列命题不正确的是( )A、过一点有无数个圆 B、过三点能作一个圆 C、三角形的外心是三角形三边的中垂线的交点 D、直角三角形的外接圆的直径为直角三角形的斜边8. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则它的外心与直角顶点的距离是( ).A、2 B、2.5 C、3 D、49. 如图,P(x,y) 是以坐标原点为圆心、5为半径的圆周上的点.若P是整点(即x,y为整数),则这样的点共有( ).
A、M点 B、N点 C、P点 D、Q点7. 下列命题不正确的是( )A、过一点有无数个圆 B、过三点能作一个圆 C、三角形的外心是三角形三边的中垂线的交点 D、直角三角形的外接圆的直径为直角三角形的斜边8. 在Rt△ABC中,∠C=90°,AC=3,BC=4,则它的外心与直角顶点的距离是( ).A、2 B、2.5 C、3 D、49. 如图,P(x,y) 是以坐标原点为圆心、5为半径的圆周上的点.若P是整点(即x,y为整数),则这样的点共有( ). A、4个 B、8个 C、12个 D、16个10. 如图,在中, , 分别作 , 两边的垂直平分线、 , 垂足分别是点M、N,以下说法:①;②;③;④点P到点B和点C的距离相等.其中正确的是( )
A、4个 B、8个 C、12个 D、16个10. 如图,在中, , 分别作 , 两边的垂直平分线、 , 垂足分别是点M、N,以下说法:①;②;③;④点P到点B和点C的距离相等.其中正确的是( )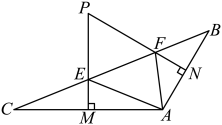 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 如图,是以原点为圆心,半径为的圆,点是直线上的一点,过点作的一条切线 , 为切点,则的最小值为 .
 12. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= , 则BD的长为
12. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= , 则BD的长为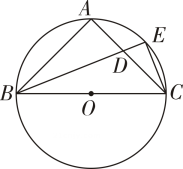 13. 如图,在直角坐标系中,一圆弧过正方形网格的格点A,B,C.已知点A的坐标为(-3,5),点B的坐标为(1,5),点C的坐标为(4,2),则该圆弧所在圆的圆心坐标为
13. 如图,在直角坐标系中,一圆弧过正方形网格的格点A,B,C.已知点A的坐标为(-3,5),点B的坐标为(1,5),点C的坐标为(4,2),则该圆弧所在圆的圆心坐标为 14. 如图,在平面直角坐标系中,已知点 , , 过原点O , 且与x轴交于另一点D , 为的切线,为切点,是的直径,则的度数为°.
14. 如图,在平面直角坐标系中,已知点 , , 过原点O , 且与x轴交于另一点D , 为的切线,为切点,是的直径,则的度数为°.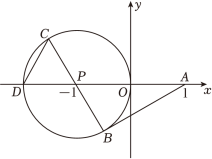 15. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .
15. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .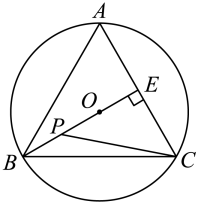
三、解答题
-
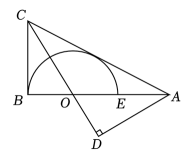
16. 如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
 (1)、求证:AB=AC;(2)、求证:DE为⊙O的切线.17. 如图,AB是⊙O的直径,点C,E在⊙O上,AC平分∠BAE,CD⊥AE交AE的延长线于点D.
(1)、求证:AB=AC;(2)、求证:DE为⊙O的切线.17. 如图,AB是⊙O的直径,点C,E在⊙O上,AC平分∠BAE,CD⊥AE交AE的延长线于点D.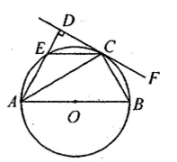 (1)、求证:CD是⊙O的切线;(2)、连接EC,若DE=1,AE=2,求EC的长.18.
(1)、求证:CD是⊙O的切线;(2)、连接EC,若DE=1,AE=2,求EC的长.18.
如图在中, , 是的角平分线,点在上,以点为圆心,长为半径的圆经过点 , 交于点 , 交于点 .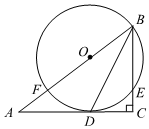 (1)、求证:是的切线;(2)、若 , , 求半径的长.19. 如图所示,已知是的直径,过的中点 , 且 .
(1)、求证:是的切线;(2)、若 , , 求半径的长.19. 如图所示,已知是的直径,过的中点 , 且 .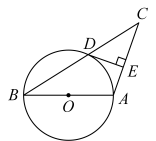 (1)、求证:是的切线;(2)、若 , cm,求的半径.20. 如图,为外一点, , 是的切线, , 为切点,点在上,连接 , , .
(1)、求证:是的切线;(2)、若 , cm,求的半径.20. 如图,为外一点, , 是的切线, , 为切点,点在上,连接 , , . (1)、求证:;(2)、连接 , 若 , 的半径为 , , 求的长.
(1)、求证:;(2)、连接 , 若 , 的半径为 , , 求的长.