2023-2024学年高中数学A版（2019）高一（上）期末测试卷

试卷更新日期：2023-12-13 类型：期末考试

进入出卷网下载

一、选择题（每题5分，共40分）

1. 设集合 $A = {x | x > 1}$ ， $B = {x | - 2 < x < 2}$ ，则 $(∁_{R} A) ∩ B =$ （）

A、 $(- 2 ， 1)$ B、 $(- 2 ， 1]$ C、 $(- \infty ， 2)$ D、 $(- \infty ， 2]$

查看试题解析
2. 命题：“ $\forall x \in R$ ， $x^{2} - 3 x + 4 < 0$ ”的否定是（）

A、 $\exists x \notin R$ ， $x^{2} - 3 x + 4 \geq 0$ B、 $\forall x \in R$ ， $x^{2} - 3 x + 4 \geq 0$ C、 $\exists x \in R$ ， $x^{2} - 3 x + 4 \geq 0$ D、 $\forall x \notin R$ ， $x^{2} - 3 x + 4 \geq 0$

查看试题解析
3. 下列函数中，既是偶函数又在 $(0 ， + \infty)$ 上单调递增的函数是（）

A、 $f (x) = x l n x$ B、 $f (x) = \frac{x^{2} + 1}{x}$ C、 $f (x) = e^{x} + e^{- x}$ D、 $f (x) = \frac{1}{x^{2} + 1}$

查看试题解析
4. 已知把物体放在空气中冷却时，若物体原来的温度是 $θ_{1} ° C$ ，空气的温度是 $θ_{0} ° C$ ，则 $t m i n$ 后物体的温度 $θ ° C$ 满足公式 $θ = θ_{0} + (θ_{1} - θ_{0}) e^{- k t}$ （其中k是一个随着物体与空气的接触状况而定的正常数）.某天小明同学将温度是 $80 ° C$ 的牛奶放在 $20 ° C$ 空气中，冷却2min后牛奶的温度是 $50 ° C$ ，则下列说法正确的是（）

A、 $k = l n 2$ B、 $k = 2 l n 2$ C、牛奶的温度降至 $35 ° C$ 还需4min D、牛奶的温度降至 $35 ° C$ 还需2min

查看试题解析
5. 已知a ， b为正实数，且 $a + 2 b = 1$ ，则 $\frac{a^{2} + 1}{a} + \frac{2 b^{2} + 1}{b}$ 的最小值为（）

A、 $1 + 2 \sqrt{2}$ B、 $2 + 2 \sqrt{2}$ C、 $3 + 2 \sqrt{2}$ D、 $4 + 2 \sqrt{2}$

查看试题解析
6. 已知 $t a n (\frac{π}{3} + θ) = \frac{3}{4}$ ，则 $s i n (2 θ + \frac{π}{6}) =$ （）

A、 $\frac{24}{25}$ B、 $\frac{7}{25}$ C、 $- \frac{7}{25}$ D、 $- \frac{24}{25}$

查看试题解析
7. 已知函数 $f (x) = {\begin{array}{l} x + \frac{1}{x} ， x > 0 \\ x + 3 ， x \leq 0 \end{array}$ ，若关于 $x$ 的方程 $f^{2} (x) - (1 + m) f (x) + m = 0$ 有四个不同的实数根，则实数 $m$ 的取值范围为（）

A、 $(- 3 ， 0)$ B、 $(0 ， 3)$ C、 $(1 ， 2]$ D、 $(2 ， 3]$

查看试题解析
8. 已知定义在R上的函数 $f (x)$ 满足 $f (x) + f (x + 1) = 0$ ，当 $x \in [3 ， 5]$ 时， $f (x) = 2 - | x - 4 |$ ，则（）

A、 B、 C、 D、

查看试题解析

二、多项选择题（每题5分，共20分）

9. 下列命题正确的是（）

A、“平面内，与一个圆只有一个公共点的直线是该圆的切线”是全称量词命题； B、命题“ $\forall x > 1$ ，都有 $x^{2} > 1$ ”的否定是“ $\exists x \leq 1 ， x^{2} \leq 1$ ”； C、“ $x > 1$ ”是“ $x > 2$ ”成立的必要不充分条件； D、幂函数 $f (x) = x^{α}$ 的图象与坐标轴没有公共点的充要条件是 $α < 0$ ．

查看试题解析
10. 已知函数 $f (x) = A s i n (ω x + φ)$ $(A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示，则下列说法正确的是（）

A、 $A = 2$ ， $ω = 2$ ， $φ = \frac{π}{3}$ B、函数 $f (x - \frac{π}{6})$ 的图象关于坐标原点对称 C、函数 $f (x)$ 的图象关于直线 $x = - \frac{17 π}{12}$ 对称 D、函数 $f (x)$ 在 $(- \frac{π}{12} ， \frac{π}{4}]$ 上的值域为 $(1 ， 2]$

查看试题解析
11. 若函数 $f (x)$ 同时满足：①对于定义域上的任意 $x$ ，恒有 $f (x) + f (- x) = 0$ ；②对于定义域上的任意 $x_{1}$ ， $x_{2}$ ，当 $x_{1} \neq x_{2}$ 时，恒 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ ，则称函数 $f (x)$ 为“理想函数”，下列四个函数中能被称为“理想函数”的是（）

A、 $f (x) = - x$ B、 $f (x) = - \sqrt[3]{x}$ C、 $f (x) = x^{3} + x$ D、 $f (x) = e^{- x} - e^{x}$

查看试题解析
12. 设函数 $f (x) = e^{x} + 2 x - 2$ ， $g (x) = 2 l n x + x - 2$ ，若 $f (a) = g (b) = 0$ ，则下列说法正确的有（）

A、 $a < \frac{1}{2}$ B、 $2 a + b = 1$ C、 $2 l n b + b = 2$ D、 $\frac{1}{a} + \frac{1}{b} = \frac{3}{2} + \sqrt{2}$

查看试题解析

三、填空题（每题5分，共20分）

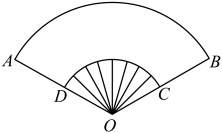
13. “数摺聚清风，一捻生秋意”是宋代朱翌描写折扇的诗句，折扇出入怀袖，扇骨雕琢，是文人雅士的宠物，如图，这是折扇的示意图，已知D为OA中点，OA＝4， $∠ A O B = \frac{3 π}{4}$ （扇环ABCD）部分的面积是．

查看试题解析
14. 已知 $t a n α = - 2$ ，则 $\frac{s i n α + 3 c o s α}{2 s i n α - c o s α} =$ ．

查看试题解析
15. 已知 $f (x)$ 是定义在 $R$ 上的奇函数，当 $x \geq 0$ 时， $f (x) = 2^{x} + x - 1$ ，则 $f (l o g_{2} \frac{1}{4})$ 的值为.

查看试题解析
16. 已知函数 $f (x) = 2 s i n (2 x + \frac{π}{3})$ 的图象向左平移 $\frac{π}{12}$ 个单位后得到函数 $g (x)$ 的图象，若实数 $x_{1}$ ， $x_{2}$ 满足 $f (x_{1}) - g (x_{2}) = 4$ ，则 $| x_{1} - x_{2} |$ 的最小值为．

查看试题解析

四、解答题（共6题，共70分）

17. 已知幂函数 $f (x) = (m + n - 2) x^{m - n} (m ， n \in N_{+})$ 在 $(- ∞ ， 0)$ 上单调递减.

(1)、求 $f (2)$ 的值；

(2)、求 $f (x^{2}) \leq f (16)$ 的解集.

查看试题解析
18. 已知 $f (α) = \frac{s i n (α - 3 π) \cdot c o s (2 π - α) \cdot s i n (- α + \frac{3}{2} π)}{c o s (- π - α) \cdot s i n (- π - α)}$ ．

(1)、化简 $f (α)$ ；

(2)、若 $α$ 为第四象限角且 $s i n α = - \frac{3}{5}$ ，求 $f (α)$ 的值；

(3)、若 $α = - \frac{31}{3} π$ ，求 $f (α)$ ．

查看试题解析
19. 已知函数 $f (x) = l o g_{2} (2^{x} + 1) + a x$ 是偶函数.

(1)、求 $a$ 的值；

(2)、设 $g (x) = f (x) + x$ ， $h (x) = x^{2} - 2 x + m$ ，若对任意的 $x_{1} \in [0 ， 4]$ ，存在 $x_{2} \in [0 ， 5]$ ，使得 $g (x_{1}) \geq h (x_{2})$ ，求 $m$ 的取值范围.

查看试题解析
20. 某公司生产一类电子芯片，且该芯片的年产量不超过35万件，每万件电子芯片的计划售价为16万元.已知生产此类电子芯片的成本分为固定成本与流动成本两个部分，其中固定成本为30万元/年，每生产 $x$ 万件电子芯片需要投入的流动成本为 $f (x)$ （单位：万元），当年产量不超过14万件时， $f (x) = \frac{2}{3} x^{2} + 4 x$ ；当年产量超过14万件时， $f (x) = 17 x + \frac{400}{x} - 80$ .假设该公司每年生产的芯片都能够被销售完.

(1)、写出年利润 $g (x)$ （万元）关于年产量 $x$ （万件）的函数解析式；（注：年利润=年销售收入-固定成本-流动成本）

(2)、如果你作为公司的决策人，为使公司获得的年利润最大，每年应生产多少万件该芯片？

查看试题解析
21. 函数 $f (x)$ 对任意实数 $x ， y$ 恒有 $f (x) = f (y) + f (x - y)$ ，且当 $x > 0$ 时， $f (x) < 0$ .

(1)、判断 $f (x)$ 的奇偶性；

(2)、求证： $f (x)$ 是 $R$ 上的减函数；

(3)、若 $a \in R$ ，解关于 $x$ 的不等式 $f (a x^{2}) + f (x + 2) < f (x^{2}) - f (a x)$ .

查看试题解析
22. 已知函数 $f (x) = 2 s i n x c o s x + 2 c o s^{2} x$ .

(1)、求 $f (0)$ 的值；

(2)、求 $f (x)$ 的最小正周期和单调递增区间；

(3)、将函数 $y = f (x)$ 的图象向右平移 $\frac{π}{8}$ 个单位，得到函数 $y = g (x)$ 的图象，若函数 $y = g (x)$ 在 $[0 ， m]$ 上有且仅有两个零点，求 $m$ 的取值范围.

查看试题解析