人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——24.1圆的性质
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )
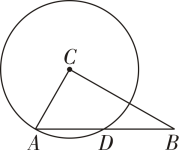 A、 B、3 C、9 D、62. 如图,A、B、C是⊙O上的三个点,∠ABC=50°,连接AO、OC.过点O作OD⊥BC 于点D.若∠OCD=40°,则∠AOD的度数为( ).
A、 B、3 C、9 D、62. 如图,A、B、C是⊙O上的三个点,∠ABC=50°,连接AO、OC.过点O作OD⊥BC 于点D.若∠OCD=40°,则∠AOD的度数为( ).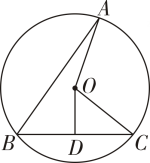 A、120° B、135° C、140° D、150°3. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( )
A、120° B、135° C、140° D、150°3. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( ) A、 B、8 C、10 D、4. 如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M , N两点,直线与相交于C , D两点,若 , 则的长为( )
A、 B、8 C、10 D、4. 如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M , N两点,直线与相交于C , D两点,若 , 则的长为( ) A、 B、4 C、 D、5. 如图,都是的半径, , 则下列结论不正确的是( )
A、 B、4 C、 D、5. 如图,都是的半径, , 则下列结论不正确的是( )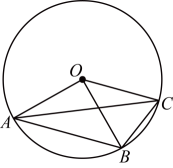 A、 B、 C、 D、6. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )
A、 B、 C、 D、6. 如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若∠ECF=60°,则∠DCF的大小是 ( )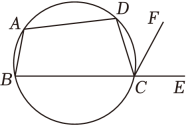 A、30° B、48° C、54° D、60°7. 如图,在⊙O中,= . 有下列结论:
A、30° B、48° C、54° D、60°7. 如图,在⊙O中,= . 有下列结论:
①AB=CD;②AC=BD;③∠AOC=∠BOD;④= .
其中正确的有( )
A、②③④ B、①②③④ C、①②④ D、①②③8. 下列说法不正确的是( )A、直径所对的圆周角是直角 B、圆的两条平行弦所夹的弧相等 C、相等的圆周角所对的弧相等 D、相等的弧所对的圆周角相等9. 如图,⊙O是△ABC的外接圆,弦BD交AC于点E,AE=DE,BC=CE,过点O作OF⊥AC于点F,延长FO交BE于点G,若DE=6,EG=4,则AB的长为( ) A、 B、 C、13 D、1410. 如图,已知是的直径,点C是弧的中点,点D在的延长线上,连接交⊙O于点E , 若 , 则( )
A、 B、 C、13 D、1410. 如图,已知是的直径,点C是弧的中点,点D在的延长线上,连接交⊙O于点E , 若 , 则( ) A、20° B、22.5° C、25° D、30°
A、20° B、22.5° C、25° D、30°二、填空题
-
11. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A,B的读数分别为86°,30°,则∠ACB的大小为
 12. 如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则的度数为
12. 如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则的度数为 13. 如图,MN是⊙O的直径,MN=2.点A在⊙O上,∠AMN=30°,B为的中点,P为直径MN上一动点,则PA+PB的最小值为
13. 如图,MN是⊙O的直径,MN=2.点A在⊙O上,∠AMN=30°,B为的中点,P为直径MN上一动点,则PA+PB的最小值为 14. 如图,四边形是的内接四边形,平分 , 连结 , , , 若等于 , 则的度数为 .
14. 如图,四边形是的内接四边形,平分 , 连结 , , , 若等于 , 则的度数为 . 15. 如图,AB 是⊙O的直径,C,D是上两点.若∠ADC=120°,则∠BAC的度数是
15. 如图,AB 是⊙O的直径,C,D是上两点.若∠ADC=120°,则∠BAC的度数是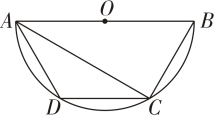
三、解答题
-
16. 如图,等腰内接于 , AC的垂直平分线交边BC于点E , 交于F , 垂足为D , 连接AF并延长交BC的延长线于点P .
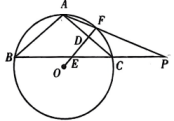 (1)、求证:;(2)、若 , 求的度数.17. 已知外接圆 , , , 求证: .
(1)、求证:;(2)、若 , 求的度数.17. 已知外接圆 , , , 求证: . 18. 如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
18. 如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.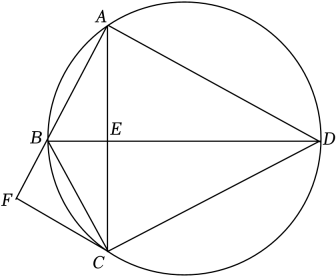 (1)、求证DB平分∠ADC , 并求∠BAD的大小;(2)、过点C作CF∥AD交AB的延长线于点F , 若AC=AD , BF=2求此圆半径的长19. 如图,AB是⊙O的直径,弦AC= , D是的中点,且CD∥AB.求CD的长.
(1)、求证DB平分∠ADC , 并求∠BAD的大小;(2)、过点C作CF∥AD交AB的延长线于点F , 若AC=AD , BF=2求此圆半径的长19. 如图,AB是⊙O的直径,弦AC= , D是的中点,且CD∥AB.求CD的长. 20. 已知:如图,AB,CD是⊙O的弦,且AB=CD,M,N分别是AB,CD的中点.求证:∠AMN=∠CNM.
20. 已知:如图,AB,CD是⊙O的弦,且AB=CD,M,N分别是AB,CD的中点.求证:∠AMN=∠CNM. 21. 如图,点A,B,C,D,E,F都在⊙O上,且AB=BC=CD=DE=EF=AF.若⊙O的半径为6,求AE的长.
21. 如图,点A,B,C,D,E,F都在⊙O上,且AB=BC=CD=DE=EF=AF.若⊙O的半径为6,求AE的长.

