人教版2023-2024年数学九年级第一学期期末扫盲清障复习卷——23.1图形的旋转
试卷更新日期:2023-12-13 类型:复习试卷
一、选择题
-
1. 如图,将绕点O旋转后得到 , ED是的中位线,旋转后为线段 . 已知 , 则( )
 A、2 B、3 C、4 D、1.52. 如图,在正方形网格中,将绕某一点旋转某一角度得到 , 则旋转中心是( )
A、2 B、3 C、4 D、1.52. 如图,在正方形网格中,将绕某一点旋转某一角度得到 , 则旋转中心是( ) A、点A B、点B C、点C D、点D3. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( )
A、点A B、点B C、点C D、点D3. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( ) A、 B、 C、 D、4. 如图,在平面直角坐标系中,△ABC绕点C(0,1)旋转180°得到△A'B'C,已知点A的坐标为(2,-1).则点A'的坐标是.( )
A、 B、 C、 D、4. 如图,在平面直角坐标系中,△ABC绕点C(0,1)旋转180°得到△A'B'C,已知点A的坐标为(2,-1).则点A'的坐标是.( )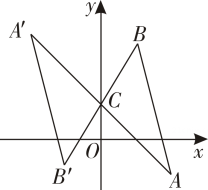 A、(- 2,1) B、(-2,3) C、(-2,-1) D、(-2,2)5. 如图,在的方格纸中,A , B两点在格点上,线段AB绕某点(旋转中心)逆时针旋转角后得到线段 , 点与A对应,则旋转中心是( )
A、(- 2,1) B、(-2,3) C、(-2,-1) D、(-2,2)5. 如图,在的方格纸中,A , B两点在格点上,线段AB绕某点(旋转中心)逆时针旋转角后得到线段 , 点与A对应,则旋转中心是( )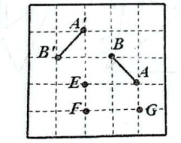 A、点B B、点G C、点E D、点F6. 如图,在中, , 将绕点逆时针旋转角度()得到 , 若 , 则的值为( )
A、点B B、点G C、点E D、点F6. 如图,在中, , 将绕点逆时针旋转角度()得到 , 若 , 则的值为( ) A、 B、 C、 D、7. 如图,是绕点顺时针旋转得到的,延长与相交于点、若 , , , 则的度数为( )
A、 B、 C、 D、7. 如图,是绕点顺时针旋转得到的,延长与相交于点、若 , , , 则的度数为( )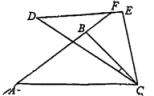 A、 B、 C、 D、8. 如图,△ABC中,∠BAC=135°,把△ABC绕着点C顺时针旋转得到△DEC,若点D、A、B恰好在一条直线上,则下列结论错误的是 ( )
A、 B、 C、 D、8. 如图,△ABC中,∠BAC=135°,把△ABC绕着点C顺时针旋转得到△DEC,若点D、A、B恰好在一条直线上,则下列结论错误的是 ( )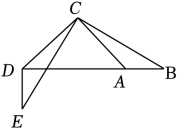 A、ED⊥BD B、△ABC≌△DEC C、 D、BD=CE+DE9. 两块完全相同的含30°角的直角三角板ABC和A'B'C′重合在一起,将三角板A'B'C'绕直角顶点C'按逆时针方向旋转α(0°<α≤90°),如图所示.以下结论错误的是( )
A、ED⊥BD B、△ABC≌△DEC C、 D、BD=CE+DE9. 两块完全相同的含30°角的直角三角板ABC和A'B'C′重合在一起,将三角板A'B'C'绕直角顶点C'按逆时针方向旋转α(0°<α≤90°),如图所示.以下结论错误的是( )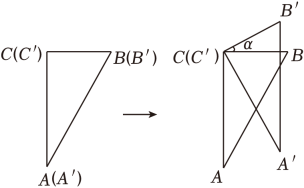 A、当α=30°时,A'C与AB的交点恰好为AB中点 B、当α=60°时,A'B'恰好经过点B C、在旋转过程中,存在某一时刻,使得AA'=BB' D、在旋转过程中,始终存在AA'⊥BB'10. 如图,将△ABC绕点A旋转到△AB1C1 , 有下列说法:
A、当α=30°时,A'C与AB的交点恰好为AB中点 B、当α=60°时,A'B'恰好经过点B C、在旋转过程中,存在某一时刻,使得AA'=BB' D、在旋转过程中,始终存在AA'⊥BB'10. 如图,将△ABC绕点A旋转到△AB1C1 , 有下列说法:
①AC=AB;②BC=B1C1;③∠BAC=∠B1AC1;④∠CAC1=∠BAB1 .
其中正确的有( ).
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,E是正方形ABCD内一点,将△ABE绕点B顺时针旋转与△CBF重合,若BE= , 则EF= .
 12. 如图,将左边的长方形绕点B按顺时针方向旋转一定角度后,位置如右边的长方形,则∠CBA的度数是
12. 如图,将左边的长方形绕点B按顺时针方向旋转一定角度后,位置如右边的长方形,则∠CBA的度数是 13. 如图,正方形ABCD中,AB=12,E是BC边上一点,CE=7,F是正方形内部一点,且EF=3,连接EF,DE,DF,并将△DEF绕点D逆时针旋转90°得到△DMN(点M、N分别为点E、F的对应点),连接CN,则CN长度的最小值为 .
13. 如图,正方形ABCD中,AB=12,E是BC边上一点,CE=7,F是正方形内部一点,且EF=3,连接EF,DE,DF,并将△DEF绕点D逆时针旋转90°得到△DMN(点M、N分别为点E、F的对应点),连接CN,则CN长度的最小值为 . 14. 如图,中, , , , 为线段上一动点,为延长线上的动点,始终保持 . 连接和 , 将绕点逆时针旋转到 , 连接 , 为中点,当从点运动到点时,点所经过的路径长为 .
14. 如图,中, , , , 为线段上一动点,为延长线上的动点,始终保持 . 连接和 , 将绕点逆时针旋转到 , 连接 , 为中点,当从点运动到点时,点所经过的路径长为 . 15. 如图,正方形边长为 , 点在边上,不与 , 重合 , 将沿直线折叠,点落在处,连接 , 将绕点顺时针旋转得到 , 连接 , , , 给出下列四个结论:
15. 如图,正方形边长为 , 点在边上,不与 , 重合 , 将沿直线折叠,点落在处,连接 , 将绕点顺时针旋转得到 , 连接 , , , 给出下列四个结论:
≌; ;点是直线上动点,则的最小值为;
当时,的面积为 ,
其中正确的结论是 填写序号
三、作图题
-
16. 如图,A,B,C三点的坐标分别为(﹣4,1),(﹣3,3),(﹣1,﹣1).

⑴将△ABC绕点O顺时针旋转90°,画出旋转后所得到的△DEF(点D,E,F分别对应点A,B,C).
⑵画出△DEF关于原点对称的图形△PMN(点P,M,N分别对应点D,E,F).
⑶直接写出△PMN的面积.
17. 如图,P是正方形ABCD内一点,连结PA,PB,PC. (1)、画出将△PAB绕点B顺时针旋转90°得到的△P'CB.(2)、若PA=2,PB=4,∠APB=135°,求PC的长.
(1)、画出将△PAB绕点B顺时针旋转90°得到的△P'CB.(2)、若PA=2,PB=4,∠APB=135°,求PC的长.四、解答题
-
18. 某学校活动小组探究了如下问题,请你帮助他们完成解答过程:
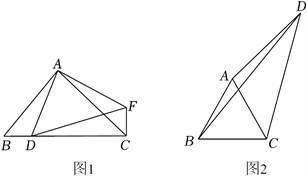 (1)、操作发现:如图1,△ABC中,AB=AC , ∠BAC=90°,D为边BC上的一点,连接AD , 作∠FAD=90°,并截取FA=AD , 连接DF . 求证:BD2+CD2=DF2;(2)、灵活运用:如图2,在四边形ABCD中,AC , BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,求CD的长.19. 已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)、操作发现:如图1,△ABC中,AB=AC , ∠BAC=90°,D为边BC上的一点,连接AD , 作∠FAD=90°,并截取FA=AD , 连接DF . 求证:BD2+CD2=DF2;(2)、灵活运用:如图2,在四边形ABCD中,AC , BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,求CD的长.19. 已知△ABC与△DEC是两个大小不同的等腰直角三角形. (1)、如图1所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;(2)、如图2所示,连接DB,将线段DB绕D点顺时针旋转90°到DF的位置,连接AF交ED于点N,试判断线段DE和AF的数量和位置关系,并说明理由.20. 在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC , 点A、B的对应点分别是D、E .
(1)、如图1所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;(2)、如图2所示,连接DB,将线段DB绕D点顺时针旋转90°到DF的位置,连接AF交ED于点N,试判断线段DE和AF的数量和位置关系,并说明理由.20. 在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC , 点A、B的对应点分别是D、E . (1)、当点E恰好在AC上时,如图1,求∠ADE的大小;(2)、若α=60°时,点F是AC中点,如图2,求证:四边形BEDF是平行四边形.21. 将两个全等的和按图1方式摆放,其中 , 点E落在上,所在直线交直线于点F .
(1)、当点E恰好在AC上时,如图1,求∠ADE的大小;(2)、若α=60°时,点F是AC中点,如图2,求证:四边形BEDF是平行四边形.21. 将两个全等的和按图1方式摆放,其中 , 点E落在上,所在直线交直线于点F . (1)、求证:;(2)、若将图1中绕点B按顺时针方向旋转到图2位置,其他条件不变(如图2),请写出此时、与之间的数量关系,并加以证明.22. 已知矩形 , , , 将矩形绕A顺时针旋转 , 得到矩形 , 点B的对应点是点E , 点C的对应点是点F , 点D的对应点是点G .
(1)、求证:;(2)、若将图1中绕点B按顺时针方向旋转到图2位置,其他条件不变(如图2),请写出此时、与之间的数量关系,并加以证明.22. 已知矩形 , , , 将矩形绕A顺时针旋转 , 得到矩形 , 点B的对应点是点E , 点C的对应点是点F , 点D的对应点是点G . (1)、如图①;当时,连接 , 求的长;(2)、如图②,当边经过点D时,延长交于点P , 求的长;(3)、连接 , 点M是的中点,连接 , 在旋转过程中,线段的最大值 .23. 我们可以通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
(1)、如图①;当时,连接 , 求的长;(2)、如图②,当边经过点D时,延长交于点P , 求的长;(3)、连接 , 点M是的中点,连接 , 在旋转过程中,线段的最大值 .23. 我们可以通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.原题:如图1,点E、F分别在正方形ABCD的边BC、CD上, , 连接EF , 则 , 试说明理由.
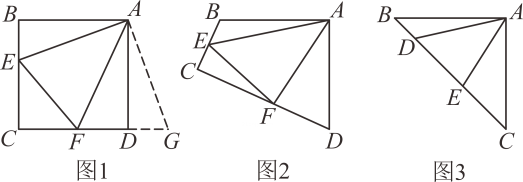 (1)、思路梳理
(1)、思路梳理,
把绕点A逆时针旋转至 , 可使AB与AD重合.
,
, 点F、D、G共线.
根据 , 易证 , 得 .
(2)、类比引申如图2,四边形ABCD中, , , 点E、F分别在边BC、CD上, , 若、都不是直角,则当与满足等量关系时,仍有 .
(3)、联想拓展如图3,在中, , , 点D、E均在边BC上,且 . 猜想BD、DE、EC应满足的等量关系,并写出推理过程.