人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——期末综合测试卷

试卷更新日期：2023-12-13 类型：期末考试

进入出卷网下载

一、选择题

1. 下列交通标志的图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一个正多边形的每个外角都等于45°，则这个多边形的边数为（）

A、4 B、6 C、8 D、10

查看试题解析
3. 小明和小红两位小朋友在做拼三角形的游戏，小明手上有两根木棒长分别为4cm和7cm ，小红手上有四根木棒，长度如下：2cm ， 3cm ， 8cm ， 12cm ，小明从小红手中选一根要能拼成一个三角形，小明应选长为（　　）的木棒．

A、2 cm B、3cm C、8cm D、12cm

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A H$ 是高， $A M$ 是中线，那么在结论① $∠ B = ∠ B A M$ ， ② $∠ B = ∠ M A H$ ， ③ $∠ B = ∠ C A H$ ， ④ $A M = \frac{1}{2} B C$ ， ⑤ $S_{A C H} = S_{A B M}$ 中错误的个数（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
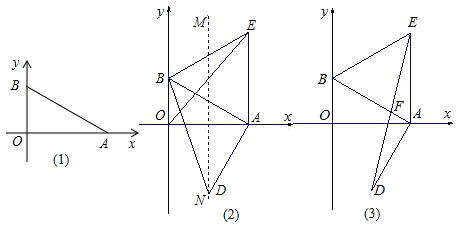
5. 如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O，与AB、AC相交于点M、N，且MN∥BC．若AB=8，AC=6，BC=10，那么△AMN的周长是（　　）

A、7 B、12 C、14 D、24

查看试题解析
6. 若(x-5) (x+m) =x²-2x+n，则m，n的值分别为（）

A、-2，18 B、3，15 C、3，-15 D、-2，-18

查看试题解析
7. 从前，古希腊一位庄园主把一块边长为a米（ $a > 10$ ）的正方形土地租给租户张老汉，第二年，他对张老汉说：“我把这块地的一边增加10米，相邻的另一边减少10米，变成一个长方形的土地继续租给你，租金不变，你也没有吃亏，你看如何？”如果这样，你觉得张老汉的租地面积会（）

A、变小了 B、变大了 C、没有变化 D、无法确定

查看试题解析
8. 分式 $\frac{x + 1}{x^{2} - x} ， \frac{2}{x^{2} - 1} ， - \frac{x}{x^{2} + 2 x + 1}$ 的最简公分母是（）

A、（x²-x）（x+1） B、（x²-1）（x+1）² C、x（x-1）（x+1）² D、x（x+1）²

查看试题解析
9. 某园林公司增加了人力进行园林绿化，现在平均每天比原计划多植树50棵，现在植树600棵所需的时间与原计划植树450棵所需的时间相同，如果设原计划平均每天植树 $x$ 棵，那么下面所列方程中，正确的是（）

A、 $\frac{600}{x - 50} = \frac{450}{x}$ B、 $\frac{600}{x + 50} = \frac{450}{x}$ C、 $\frac{600}{x} = \frac{450}{x + 50}$ D、 $\frac{600}{x} = \frac{450}{x - 50}$

查看试题解析
10. 如图，AB＝AD，∠BAD＝140°，AB⊥CB于点B，AD⊥CD于点D，E、F分别是CB、CD上的点，且∠EAF＝70°，下列结论中①DF＝BE，②△ADF≌△ABE，③FA平分∠DFE，④EF平分∠AEC，⑤BE+DF＝EF．其中正确的结论是（）

A、④⑤ B、①② C、③⑤ D、①②③

查看试题解析

二、填空题

11. 若式子 $\frac{| a | - 2}{a + 2}$ 的值为0，则 $a$ 的值为.

查看试题解析
12. 如图，点D、E分别在等边△ABC的边AB、BC上，将△BDE沿直线DE翻折，使点B落在点B处，DB，、EB、分别交边AC于点F、G，若∠ADF =84°，则∠CEG=度．

查看试题解析
13. 如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（ -2，0），点A的坐标为（-6，3），则B点的坐标是

查看试题解析
14. 若代数式x²-8x+m是关于x的完全平方式。则实数m= ．

查看试题解析
15. 如图，在平面直角坐标系xOy中，A（2，0），B（10，0），点P为y轴正半轴上的一个动点，以线段PA为边在PA的右上方作等边△APQ ，连接QB ，在点P运动的过程中，线段QB长度的最小值为．

查看试题解析

三、计算题

16. 分解因式

(1)、 $4 a^{3} b - 2 a^{2} b^{2}$

(2)、 $x^{2} - 4 x + 4$

(3)、 $2 m^{2} - 18$

(4)、 $a^{2} + 7 a - 18$

查看试题解析
17. 计算：

(1)、 $- 1^{2} - {(- 2)}^{3} \div 4 + {(\frac{1}{2})}^{- 2} - | - 2 | + {(3 - π)}^{0}$ ．

(2)、 $(3 x + 2) (3 x - 2) - 5 x (x - 1) - {(2 x - 1)}^{2}$

查看试题解析
18. 解方程

(1)、 $\frac{1}{x} = \frac{2}{x + 1}$

(2)、 $\frac{x - 2}{x + 2} - \frac{16}{x^{2} - 4} = 1$

查看试题解析

四、解答题

19. 某蔬菜店第一次用 $800$ 元购进某种蔬菜，由于销售状况良好，该店又用 $1400$ 元第二次购进该品种蔬菜，所购数量是第一次购进数量的 $2$ 倍，但进货价每千克少了 $0.5$ 元．

(1)、第一次所购该蔬菜的进货价是每千克多少元？

(2)、蔬菜店在销售中，如果两次售价均相同，第一次购进的蔬菜有 $3 %$ 的损耗，第二次购进的蔬菜有 $5 %$ 的损耗，若该蔬菜店售完这些蔬菜获利不低于 $1244$ 元，则该蔬菜每千克售价是多少元？

查看试题解析
20. 先化简，再求值：
$(\frac{m + 1}{m - 1} + 1) \div \frac{m + m^{2}}{m^{2} - 2 m + 1} - \frac{2 - 2 m}{m^{2} - 1}$ ，其中 $m$ 满足 $- 2 \leq m \leq 2$ ，取一个整数即可.

查看试题解析
21. 仔细阅读下面例题，解答问题：
例题：已知二次三项式 x² - 4x + m 有一个因式是(x+3)，求另一个因式以及 m 的值．
解：设另一个因式为(x+n)，得 x² - 4x + m = ( x + 3)( x + n)
则 x² - 4x + m = x² + (n + 3) x + 3n
∴ ${\begin{matrix} n + 3 = - 4 \\ m = 3 n \end{matrix}$
解得：n=－7，m=－21
∴另一个因式为(x－7)，m 的值为－21．
问题：仿照以上方法解答下面问题：
已知二次三项式 2x² + 3x - k 有一个因式是(2x－3)，求另一个因式以及 k 的值．

查看试题解析
22. 如图，平面直角坐标系中，点A、B分别在x、y轴上，点B的坐标为（0，1），∠BAO=30°．

(1)、求AB的长度；

(2)、以AB为一边作等边△ABE，作OA的垂直平分线MN交AB的垂线AD于点D．求证：BD=OE；

(3)、在（2）的条件下，连接DE交AB于F．求证：F为DE的中点．

查看试题解析
23. 如图，△ABC和△AOD是等腰直角三角形，AB=AC，AO=AD，∠BAC=∠OAD=90°，点O是△ABC内的一点，∠BOC=130°．

(1)、求证：OB=DC；

(2)、求∠DCO的大小；

(3)、设∠AOB=α，那么当α为多少度时，△COD是等腰三角形．

查看试题解析