人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——第十四章综合测试
试卷更新日期:2023-12-13 类型:单元试卷
一、选择题
-
1. 若a2-b2=4,a-b=-2,则a+b的值为( )A、2 B、1 C、-0.5 D、-22. 已知 , 则 , 的值分别为( )A、 , B、 , C、 , D、 ,3. 若计算的结果中不含仿项,则的值为( )A、2 B、0 C、 D、4. 若3x=15,3y=5,则3x﹣y等于( )A、10 B、5 C、15 D、35. 如图,在一块长 , 宽的长方形空地上,修建同样宽的两条互相垂直的道路两条道路各与长方形的一条边垂直 , 剩余部分栽种花草美化环境,设道路的宽度为 , 则栽种花草的面积表示不正确的是( )
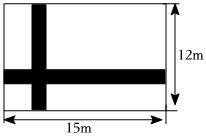 A、 B、 C、 D、6. 已知 , 则代数式的值是( )A、 B、 C、 D、7. 计算的结果是( )A、 B、 C、 D、8. 若满足 , 则( )A、 B、 C、 D、9. 已知a+ =3,则a2+ 的值是( )A、9 B、7 C、5 D、310. 若 , 则 A 为 ( )A、 B、 C、 D、
A、 B、 C、 D、6. 已知 , 则代数式的值是( )A、 B、 C、 D、7. 计算的结果是( )A、 B、 C、 D、8. 若满足 , 则( )A、 B、 C、 D、9. 已知a+ =3,则a2+ 的值是( )A、9 B、7 C、5 D、310. 若 , 则 A 为 ( )A、 B、 C、 D、二、填空题
-
11. 若am= 4,a2m+n= 128,则an=12. 若要使4x2+mx+成为一个两数差的完全平方式,则m的值应为13. 若2x+3·3x+3=36x-2 , 则x=14. 若是多项式的一个因式,则k的值是.15. 已知m、n互为相反数,且满足 , 则的值是.
三、计算题
-
16. 因式分解.(1)、4a2x-12ax+9x(2)、(2x+y)2-y217. 因式分解:(1)、4ab-2a2b;(2)、25x2-9y2;(3)、2a2b-8ab2+8b3;(4)、x2(x-3)+9(3-x).
四、解答题
-
18. 观察下列算式特征,并完成相应任务.
;
;
;
.
(1)、任务一:发现与表达请用含字母的算式表示以上算式的一般特征: .
(2)、任务二:问题与解决如果 , 其中 , , 均为整数,则的取值有____ .
A、1个 B、2个 C、3个 D、4个(3)、任务三:拓展与猜想若 , 则 , .
19. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式。例如图1可以得到(a+b)2 =a2 +2ab+b2 , 请解答下列问题:
 (1)、图2所表示的数学等式为(2)、利用(1)得到的结论,解决问题:若a+b+c=12,a2+b2+c2 =60,求ab+ac+bc的值;(3)、如图3,将两个边长分别为a和b的正方形拼在一起,B,C,D三点在同一直线上,连接AE、EG,若两正方形的边长满足a+b=15,ab=35,求阴影部分面积.20. 求(2-1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1的个位数字.
(1)、图2所表示的数学等式为(2)、利用(1)得到的结论,解决问题:若a+b+c=12,a2+b2+c2 =60,求ab+ac+bc的值;(3)、如图3,将两个边长分别为a和b的正方形拼在一起,B,C,D三点在同一直线上,连接AE、EG,若两正方形的边长满足a+b=15,ab=35,求阴影部分面积.20. 求(2-1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1的个位数字.