人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——第十三章综合测试
试卷更新日期:2023-12-13 类型:单元试卷
一、选择题
-
1. 下列图案或文字中,是轴对称图形的有( )
 A、2个 B、3个 C、4个 D、5个2. 如图,在△ABC中,AB=AC , ∠ABC=75°,BD是AC边上的高,则∠ABD的度数为( )
A、2个 B、3个 C、4个 D、5个2. 如图,在△ABC中,AB=AC , ∠ABC=75°,BD是AC边上的高,则∠ABD的度数为( ) A、15° B、30° C、60° D、75°3. 如图,在中, , , 分别以、为圆心,4为半径画弧交于两点,过这两点的直线交AC于点 , 连接BD , 则的周长为( )
A、15° B、30° C、60° D、75°3. 如图,在中, , , 分别以、为圆心,4为半径画弧交于两点,过这两点的直线交AC于点 , 连接BD , 则的周长为( ) A、12 B、11 C、10 D、84. 如图,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F,若∠EPF=110°,则∠AOB的度数是 ( )
A、12 B、11 C、10 D、84. 如图,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F,若∠EPF=110°,则∠AOB的度数是 ( ) A、35° B、40° C、70° D、80°5. 下列条件不能得到等边三角形的是( )A、有两个内角是的三角形 B、有一个角是的等腰三角形 C、腰和底相等的等腰三角形 D、有两个角相等的等腰三角形6. 关于点 , 下列说法正确的个数有( )
A、35° B、40° C、70° D、80°5. 下列条件不能得到等边三角形的是( )A、有两个内角是的三角形 B、有一个角是的等腰三角形 C、腰和底相等的等腰三角形 D、有两个角相等的等腰三角形6. 关于点 , 下列说法正确的个数有( )
①点到轴的距离为;
②点到轴的距离为;
③点在第四象限;
④点到原点的距离为;
⑤点关于轴的对称点的坐标是 .A、个 B、个 C、个 D、个7. 如图,在△ABC中,AB⊥AC , AB=3,BC=5,AC=4,EF垂直平分BC , 点P为直线EF上的任意一点,则△ABP周长的最小值是( ) A、12 B、6 C、7 D、88. 如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )
A、12 B、6 C、7 D、88. 如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )①AD平分∠EDF;②△EBD≌△FCD;③BD=CD;④AD⊥BC.
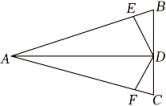 A、1个 B、2个 C、3个 D、4个9. 如图,在中, , , 平分交于点 , 交于点 , 下列四个结论:
A、1个 B、2个 C、3个 D、4个9. 如图,在中, , , 平分交于点 , 交于点 , 下列四个结论:
;
点在的垂直平分线上;
图中共有个等腰三角形;
≌;
其中正确的结论有( )
A、个 B、个 C、个 D、个10. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作正三角形ABC和正三角形CDE , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q , 连接PQ . 以下四个结论:①AD=BE;②∠AOB=60°;③AP=BQ;④连接CO , 则AO=BO+CO . 恒成立的结论有( )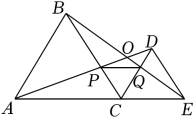 A、①②③ B、①② C、②③④ D、①②③④
A、①②③ B、①② C、②③④ D、①②③④二、填空题
-
11. 点A(3,-1)关于y轴对称的点的坐标是 .12. 如图,△ABC中,BC的垂直平分线l与AC相交于点D,若△ABD的周长为12cm,
则AB+AC=cm.
 13. 如图,等腰△ABC的底边BC=20,面积为120,点D在BC边上,且CD=5,直线EF是腰AC的垂直平分线,若点M在EF上运动,则△CDM周长的最小值为 .
13. 如图,等腰△ABC的底边BC=20,面积为120,点D在BC边上,且CD=5,直线EF是腰AC的垂直平分线,若点M在EF上运动,则△CDM周长的最小值为 .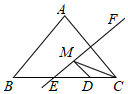 14. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠A=°.
14. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠A=°. 15. 如图,OP是∠MON的平分线,点A是ON上一点,作线段OA的垂直平分线交OM于点B,过点A作CA⊥ON交OP于点C,连接BC,AB=10,CA=4,则∆OBC面积为.
15. 如图,OP是∠MON的平分线,点A是ON上一点,作线段OA的垂直平分线交OM于点B,过点A作CA⊥ON交OP于点C,连接BC,AB=10,CA=4,则∆OBC面积为.
三、解答题
-
16. 如图,在中,于点D.
 (1)、求证:(2)、若 AF 平分分别交CD、BC于 点E、F,求证:是等腰三角形.17. 在边长为9cm的等边三角形ABC中,点Q是BC边上的一点,动点P以1cm/s的速度从点A沿AB向点B运动,设运动时间为t(s).
(1)、求证:(2)、若 AF 平分分别交CD、BC于 点E、F,求证:是等腰三角形.17. 在边长为9cm的等边三角形ABC中,点Q是BC边上的一点,动点P以1cm/s的速度从点A沿AB向点B运动,设运动时间为t(s). (1)、如图①,若BQ=6,PQ∥AC,求t的值;(2)、如图②,若点P从点A向点B运动的同时,点Q以2cm/s的速度从点B沿BC-CA向点A运动,求t为何值时,OAPQ是等边三角形;(3)、如图③,将边长为9cm的等边三角形ABC变换为以AB、AC为腰、BC为底的等腰三角形,且AB=AC=10cm,BC=8cm,点P运动到AB的中点处停止.点P停止运动后,点M以1cm/s的速度从点B沿BC向点C运动,同时点N以acm/s的速度从点C沿CA向点A运动,当△BPM与△CNM全等时,直接写出a的值.18. 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点O是线段AD上一点,点P是BA延长线上一点,且OP=OC.
(1)、如图①,若BQ=6,PQ∥AC,求t的值;(2)、如图②,若点P从点A向点B运动的同时,点Q以2cm/s的速度从点B沿BC-CA向点A运动,求t为何值时,OAPQ是等边三角形;(3)、如图③,将边长为9cm的等边三角形ABC变换为以AB、AC为腰、BC为底的等腰三角形,且AB=AC=10cm,BC=8cm,点P运动到AB的中点处停止.点P停止运动后,点M以1cm/s的速度从点B沿BC向点C运动,同时点N以acm/s的速度从点C沿CA向点A运动,当△BPM与△CNM全等时,直接写出a的值.18. 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点O是线段AD上一点,点P是BA延长线上一点,且OP=OC. (1)、请直接写出线段OB和OP之间的数量关系:(2)、请说明:∠APO+∠DCO=30° ;(3)、请说明:△POC是等边三角形;(4)、请直接写出线段AB、OA、AP之间的数量关系.19. 如图,△ABC三个顶点的坐标分别为A(-4,1),B(-3,3),C(-1,2).
(1)、请直接写出线段OB和OP之间的数量关系:(2)、请说明:∠APO+∠DCO=30° ;(3)、请说明:△POC是等边三角形;(4)、请直接写出线段AB、OA、AP之间的数量关系.19. 如图,△ABC三个顶点的坐标分别为A(-4,1),B(-3,3),C(-1,2).
⑴作出△ABC关于y轴对称的△A′B′C′,并写出C′的坐标;
⑵求出△A′B′C′的面积;
⑶在x轴上画出点P , 使PA+PC最小,并写出点P的坐标.(不写作法,保留作图痕迹)
20. 如图,在中,边的垂直平分线交于点 , 边的垂直平分线交于点 , 与相交于点 , 连接 , , 若的周长为 , 的周长为 .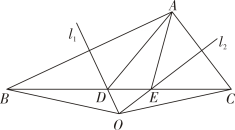 (1)、求线段的长;(2)、连接 , 求线段的长;(3)、若 , 求的度数.21.
(1)、求线段的长;(2)、连接 , 求线段的长;(3)、若 , 求的度数.21. (1)、如图 , 两个等腰三角形和中, , , , 连接 , 则≌ , 此时线段和线段的数量关系是;(2)、如图 , 两个等腰直角三角形和中, , , , 连接 , , 两线交于点 , 请判断线段和线段的关系,并说明理由;(3)、如图 , 分别以的两边 , 为边向外作等边和等边 , 连接 , , 两线交于点请直接写出线段和线段的数量关系及的度数.22. 如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一点,连接BD,EC⊥AC,且AE=BD,连接AE交BC于点F,交BD于点H.
(1)、如图 , 两个等腰三角形和中, , , , 连接 , 则≌ , 此时线段和线段的数量关系是;(2)、如图 , 两个等腰直角三角形和中, , , , 连接 , , 两线交于点 , 请判断线段和线段的关系,并说明理由;(3)、如图 , 分别以的两边 , 为边向外作等边和等边 , 连接 , , 两线交于点请直接写出线段和线段的数量关系及的度数.22. 如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一点,连接BD,EC⊥AC,且AE=BD,连接AE交BC于点F,交BD于点H. (1)、求证:CE=AD;(2)、当AD=CF时,求证:H是AF的中点.23. 在中, , , 过点作使点 , , 按顺时针的顺序排列 , 过点作直线直线 , 垂足为点 , 直线交直线于点 , 连接 .
(1)、求证:CE=AD;(2)、当AD=CF时,求证:H是AF的中点.23. 在中, , , 过点作使点 , , 按顺时针的顺序排列 , 过点作直线直线 , 垂足为点 , 直线交直线于点 , 连接 . (1)、如图 , 若 , 的边都在的内部,作点关于的对称点 .
(1)、如图 , 若 , 的边都在的内部,作点关于的对称点 .▲ , ▲ ;填“”“”或“”
求证: .
(2)、如图 , 若 , 的边都在的外部,当 , , 的面积为时,请直接写出的长;(3)、若 , 有一条边在的内部,请直接写出线段 , , 之间的等量关系.