人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——14.3因式分解

试卷更新日期：2023-12-13 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列式子从左到右的变形，属于因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $x^{2} + 2 x - 1 = x (x + 2) - 1$ C、 $a^{2} b + a b^{2} = a b (a + b)$ D、 $a (a + b) = a^{2} + a b$

查看试题解析
2. 下列因式分解正确的是（）

A、 $a x + y = a (x + y)$ B、 $x^{2} + x - 2 = x (x + 1) - 2$ C、 $2 x^{2} - x = x (2 x - 1)$ D、 $x^{2} - 16 = {(x - 4)}^{2}$

查看试题解析
3. 下列各式中，能用公式法分解因式的有（）
①-x²-y²；②- $\frac{1}{4}$ a²b²+1；③a²+ab+b²；④-x²+2xy-y²；⑤ $\frac{1}{4}$ -mn+m²n² ．

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 已知多项式 2x³-x²＋m 分解因式后有一个因式是 x＋1，则 m 的值为（）

A、－3 B、3 C、1 D、-1

查看试题解析
5. 下列多项式中能用完全平方公式分解的是（）

A、x²-x+1 B、1-2x+x² C、a²+a+ $\frac{1}{2}$ D、-a²+b²-2ab

查看试题解析
6. 已知 $d = x^{4} - 2 x^{3} + x^{2} - 12 x - 5$ ，则当 $x^{2} - 2 x - 5 = 0$ ， $d$ 的值为（）

A、25 B、20 C、15 D、10

查看试题解析
7. 若a²+2ab+b²-c²＝10，a+b+c＝5，则a+b-c的值是（　　）

A、2 B、5 C、20 D、9

查看试题解析
8. 将几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式．例如，由图（1）可得等式： $x^{2} + (p + q) x + p q = (x + p) (x + q)$ ．将图（2）所示的卡片若干张进行拼图，可以将二次三项式 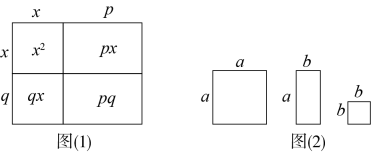$a^{2} + 3 a b + 2 b^{2}$ 分解因式为（）

A、 $(a + b) (2 a + b)$ B、 $(a + b) (3 a + b)$ C、 $(a + b) (a + 2 b)$ D、 $(a + b) (a + 3 b)$

查看试题解析
9. 已知 $x ， y ， z$ 是正整数， $x > y$ ，且 $x^{2} - x y - x z + y z = 23$ ，则 $x - z$ 等于（）

A、-1 B、1或23 C、1 D、-1或23

查看试题解析
10. 若长和宽分别是 $a ， b$ 的长方形的周长为10，面积为4，则 $a^{2} b + a b^{2}$ 的值为（）

A、14 B、16 C、20 D、40

查看试题解析

二、填空题

11. 若a＝b+2，则代数式a²-2ab+b²的值为．

查看试题解析
12. 观察下列各式： $\frac{1}{1 \times 3} = \frac{1}{2} (1 - \frac{1}{3})$ ， $\frac{1}{3 \times 5} = \frac{1}{2} (\frac{1}{3} - \frac{1}{5})$ ， $\frac{1}{5 \times 7} = \frac{1}{2} (\frac{1}{5} - \frac{1}{7})$ ， .....，根据观察，计算； $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + ⋯ + \frac{1}{4 n^{2} - 1}$ 的结果是（n为正整数）.

查看试题解析
13. 分解因式x²+ax+b ，甲看错了a值，分解的结果是（x-3）（x+2），乙看错了b值，分解的结果是（x-2）（x-3），那么x²+ax+b分解因式正确的结果应该是．

查看试题解析
14. 对于a ， b ， c ， d ，规定一种运算 $| \begin{array}{l} a & b \\ c & d \end{array} |$ ＝ad-bc ，如 $| \begin{array}{l} 1 & 2 \\ 3 & 4 \end{array} |$ ＝1×4-2×3＝-2，那么因式分解 $∣ \begin{array}{l} x & - 3 \\ 3 & x - 6 \end{array} |$ 的结果是．

查看试题解析
15. 在实数范围内分解因式 $a^{4}$ ﹣64＝．

查看试题解析

三、计算题

16. 把下列各式分解因式：

(1)、 $a^{4} - 8 a^{2} b^{2} + 16 b^{4}$

(2)、 $2 a (x - y)^{2} - 20 a (x - y) + 50 a$

(3)、 $16 (a + b)^{2} - 4 (a - b)^{2}$

(4)、 $(a^{2} + 2 a)^{2} - 2 (a^{2} + 2 a) - 3$

查看试题解析
17. 把下列各式分解因式：

(1)、6ab³－24a³b；

(2)、x⁴－8x²＋16；

(3)、a²（x＋y）－b²（y＋x）

(4)、4m²n²－（m²＋n²）²

查看试题解析

四、解答题

18. 已知在⊿ABC中,三边长a、b、c ,满足等式a²-16b²-c²+6ab+10bc=0，求证：a+c=2b.

查看试题解析
19. 观察下列分解因式的过程： $x^{2} + 2 x y - 3 y^{2}$
解：原式 $= x^{2} + 2 x y + y^{2} - y^{2} - 3 y^{2}$
$= (x^{2} + 2 x y + y^{2}) - 4 y^{2}$
$= {(x + y)}^{2} - {(2 y)}^{2}$
$= (x + y + 2 y) (x + y - 2 y)$
$= (x + 3 y) (x - y)$
像这种通过增减项把多项式转化成适当的完全平方形式的方法，在代数计算与推理中往往能起到巧妙解题的效果.

(1)、请你运用上述方法分解因式： $x^{2} + 4 x y - 5 y^{2}$ ；

(2)、若 $M = 2 (3 x^{2} + 3 x + 1)$ ， $N = 4 x^{2} + 2 x - 3$ ，比较M、N的大小，并说明理由；

(3)、已知 $R t △ A B C$ 中， $∠ C = 90 °$ ，三边长a ， b ， c满足 $c^{2} + 25 = 8 a + 6 b$ ，求 $△ A B C$ 的周长.

查看试题解析
20. 两位同学将一个关于x的二次二项式ax²+bx+c分解因式时，甲同学因看错了一次项系数而分解成2（x-1）（x-9），乙同学因看错了常数项而分解成2（x-2）（x-4）．

(1)、求原来的二次三项式；

(2)、将原来的二次三项式分解因式．

查看试题解析
21. 已知 $x^{2} + 2 x + 1$ 是多项式 $x^{3} - x^{2} + a x + b$ 的一个因式，求a，b的值，并将该多项式因式分解.

查看试题解析
22. 如果n是正整数，求证：3ⁿ⁺²-2ⁿ⁺²+3ⁿ-2ⁿ能被10整除.

查看试题解析
23. 先阅读下列材料，再解答问题：
常用的分解因式的方法有提取公因式法和公式法，但有的多项式只用上述一种方法无法分解，例如多项式 $x^{2} - x y + 4 x - 4 y$ 和 $a^{2} - b^{2} - c^{2} + 2 b c$ ．经过细心观察可以发现，若将多项式进行合理分组后，先将每一组进行分解，分别分解后再用提公因式法或公式法就可以完整分解了.

解答过程如下：
（1） $x^{2} - x y + 4 x - 4 y$

$= (x^{2} - x y) + (4 x - 4 y)$

$= x (x - y) + 4 (x - y)$

$= (x - y) (x + 4)$

（2） $a^{2} - b^{2} - c^{2} + 2 b c$

$= a^{2} - (b^{2} + c^{2} - 2 b c)$

$= a^{2} - {(b - c)}^{2}$

$= (a + b - c) (a - b + c)$

这种方法叫分组分解法，对于超过三项的多项式往往考虑这种方法．利用上述思想方法，把下列各式分解因式：
① $m^{3} - 2 m^{2} - 3 m + 6$
② $x^{2} - 2 x y - 9 + y^{2}$

查看试题解析