人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——14.2乘法公式

试卷更新日期：2023-12-13 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列去括号或添括号的变形中，正确的是（）

A、 $2 a - (3 b + c) = 2 a - 3 b + c$ B、 $a + 2 (2 b - 1) = a + 4 b - 1$ C、 $a + 4 b - 2 c = a + 2 (2 b - c)$ D、 $a - b - c = a - (b - c)$

查看试题解析
2. 四个全等的直角三角形纸片围成一个大正方形 $A B C D$ ，中间是一个小正方形 $E F G H$ ，连接四条线段 $A H$ ， $B E$ ， $C F$ ， $D G$ 得到如图所示的图形，已知每个直角三角形纸片两条直角边长分别 $a$ ， $b$ （即 $D E = a$ ， $A E = b$ ），图中阴影部分的面积为 $S$ ，则 $S$ 的值为（）

A、 $a^{2} - b^{2}$ B、 $a^{2} + b^{2}$ C、 $a^{2} - 2 a b + b^{2}$ D、 $a^{2} + 2 a b - b^{2}$

查看试题解析
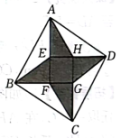3. 下列不能用平方差公式运算的是（）

A、（x+1）（x-1）． B、（-x+1）（-x-1）． C、（x+1）（-x+1）． D、（x+1）（1+x）．

查看试题解析
4. 如图，正方形ABCD和长方形AEFG的面积相等，且四边形BEFH也是正方形，欧几里得在《几何原本》中利用该图得到了：BH²=CH×GH．设AB=a，CH=b.若ab=5，则图中阴影部分的周长是（　　）

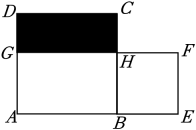A、6 B、8 C、10 D、20

查看试题解析
5. 已知 $x^{2} = 2 y + 7$ ， $y^{2} = 2 x + 7$ ，且 $x \neq y$ ，则xy的值为（）

A、7 B、3 C、-3 D、-7

查看试题解析
6. 已知x²+2mx+16（m为常数）是一个完全平方式，则m的值为（）

A、4． B、-4． C、±4． D、±8．

查看试题解析
7. 已知(2021-a) (2020-a) =4，则(2021-a)²+ (2020-a)²的值为（）

A、9 B、8 C、7 D、12

查看试题解析
8. 若 $M = 2 x^{2} + 5 x y - 3 y^{2}$ ， $N = x^{2} + 3 x y - 4 y^{2}$ ，则 $M$ 与 $N$ 的大小关系为（）

A、 $M > N$ B、 $M < N$ C、 $M \geq N$ D、 $M \leq N$

查看试题解析
9. 若 $a - \frac{1}{a} = 3$ ，则 $(a + \frac{1}{a})^{2}$ 的值是（）

A、 $5$ B、 $6$ C、 $12$ D、 $13$

查看试题解析
10. 已知 $\frac{1}{4} m^{2} + \frac{1}{4} n^{2} = n - m - 2$ ，则 $\frac{1}{m} - \frac{1}{n}$ 的值等于（）

A、1 B、0 C、 $- 1$ D、 $- \frac{1}{4}$

查看试题解析

二、填空题

11. 已知 $x^{2} - y^{2} = 8$ ，且 $x + y = 4$ ，则 $x - y =$ ．

查看试题解析
12. 若 $x + 2 y = 5$ ．则 $2 x^{2} + 8 x y + 8 y^{2} - 3 =$ ．

查看试题解析
13. 若 $4 a^{2} - 2 b = 7$ ， $b^{2} + 12 a = - 17$ ，则 $2 a - b =$ ．

查看试题解析
14. 两个正方形的边长分别为a和b，且a+b=10，ab=22 ，那么阴影部分的面积是．

查看试题解析
15. 已知a＝2023x+2023，b＝2023x+2024，c＝2023x+2025，则a²+b²+c²-ab-ac-bc的值是．

查看试题解析

三、计算题

16.

(1)、计算： $7 x^{2} y \cdot (- 2 x^{3} y^{2})$ ；

(2)、计算： $(2 a + 3 b) (a - 2 b) - \frac{1}{8} a (4 a - 3 b)$ ；

(3)、用简便方法计算： ${(- 0.125)}^{2023} \times 2^{2024} \times 4^{2024}$

(4)、先化简，再求值 $[{(x + 3 y)}^{2} - 3 (2 y - x) (x + 2 y) + 3 y^{2}] \div 2 x$ ，其中 $x = - 2 ， y = \frac{1}{3}$ ．

查看试题解析
17. 运用乘法公式计算：

(1)、 $(2 m - 3 n) (- 2 m - 3 n) - (2 m - 3 n)^{2}$

(2)、 $10 0^{2} - 9 9^{2} + 9 8^{2} - 9 7^{2} + \dots + 2^{2} - 1^{2}$ ．

查看试题解析
18. 计算

(1)、 $(x + 3 y - 2) (x - 3 y - 2)$

(2)、 ${(3 a b + 4)}^{2} - {(3 a b - 4)}^{2}$

查看试题解析

四、解答题

19. 阅读下列材料，并完成相应的任务．

材料1：①一个数的平方一定是非负数，如 $a^{2} \geq 0 ， {(a + b)}^{2} \geq 0$ ；②两个非负数的和也是非负数，如 $a^{2} + b^{2} \geq 0$ ；③一个非负数与一个正数的和是正数，如 $a^{2} + 1 > 0$ ．

材料2：若 $A - B > 0$ ，则 $A > B$ ；若 $A - B = 0$ ，则 $A = B$ ；若 $A - B < 0$ ，则 $A < B$ ．

材料3：利用 $a^{2} + 2 a b + b^{2} = {(a + b)}^{2}$ 可以将一个代数式 $x^{2} + b x + c$ 化为 ${(x + h)}^{2} + k$ 的形式．

任务：

(1)、将

x^{2} + 4 x - 3

化为

{(x + h)}^{2} + k

的形式．

(2)、比较

A = x^{2} + 2 x - 6 y

与

B = - y^{2} + 4 x - 11

的大小．

查看试题解析

20. 已知(a+b)²=17，(a- b)²=13，
求：

(1)、a²+b²的值；

(2)、ab的值．

查看试题解析
21. 阅读材料，解决后面的问题：
若 $m^{2} + 2 m n + 2 n^{2} - 6 n + 9 = 0$ ，求 $m - n$ 的值．
解： $∵ m^{2} + 2 m n + 2 n^{2} - 6 n + 9 = 0$ ，
$∴ (m^{2} + 2 m n + n^{2}) + (n^{2} - 6 n + 9) = 0$ ，
即： $(m + n)^{2} + (n - 3)^{2} = 0$ ， $∴ m + n = 0$ ， $n - 3 = 0$ ，
解得： $m = - 3$ ， $n = 3$ ， $∴ m - n = - 3 - 3 = - 6$ ．

(1)、若 $x^{2} + y^{2} + 6 x - 8 y + 25 = 0$ ，求 $x + 2 y$ 的值；

(2)、已知等腰 $△ A B C$ 的两边长 $a$ ， $b$ ，满足 $a^{2} + b^{2} = 10 a + 12 b - 61$ ，求该 $△ A B C$ 的周长；

(3)、已知正整数 $a$ ， $b$ ， $c$ 满足不等式 $a^{2} + b^{2} + c^{2} + 36 < a b + 6 b + 10 c$ ，求 $a + b - c$ 的值．

查看试题解析
22. 如图，长方形拼图，白色部分均由长为 $a$ 、宽为 $b$ 的小长方形卡片拼成．

(1)、如图1，当图中最大长方形的宽为 $20 c m$ 时，分别求 $a$ 、 $b$ 的值；

(2)、如图2，若大正方形的面积为81，每张卡片的面积为14，求小正方形的边长；

(3)、如图3，当两个阴影部分（均为长方形）面积差为定值时，求 $a$ 与 $b$ 的数量关系．

查看试题解析
23. 我们知道完全平方公式是 $(a + b)^{2} = a^{2} + 2 a b + b^{2} ， (a - b)^{2} = a^{2} - 2 a b + b^{2}$ ，由此公式我们可以得出以下结论：① $(a - b)^{2} = (a + b)^{2} - 4 a b$ ；② $a b = \frac{1}{2} [(a + b)^{2} - (a^{2} + b^{2})]$ ；利用公式①和②解决下列问题：

(1)、若 $m + n = 10 ， m n = - 3$ ，求 $(m - n)^{2}$ 的值．

(2)、若 $m$ 满足 $(2023 - 2 m)^{2} + (2 m - 2024)^{2} = 7$ ，求 $(2023 - 2 m) (2 m - 2024)$ 的值．

查看试题解析