人教版2023-2024年数学八年级第一学期期末扫盲清障复习卷——14.1整式的乘除

试卷更新日期：2023-12-13 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列运算正确的（）

A、a³-a²= a B、a²·a³=a⁶ C、（a³）²=a⁶ D、（3a）³= 9a³

查看试题解析
2. 已知（x+m）（x-5）=x²-3x+k．则k，m的值分别是（）

A、k=10，m=2 B、k=10，m=-2 C、k=-10，m=-2 D、k=-10，m=2

查看试题解析
3. 使（x²+mx）（x²-2x+n）的乘积不含x³和x² ，则m、n的值为（　　）

A、m＝0，n＝0 B、m＝-2，n＝-4 C、m＝2，n＝4 D、m＝-2，n＝4

查看试题解析
4. 已知9^m＝4，27ⁿ＝10，则3²^m⁺³ⁿ＝（　　）

A、14 B、30 C、40 D、60

查看试题解析
5. 给出下列等式： $① (a + 2 b)^{4} (- 2 b - a)^{5} = (a + 2 b)^{9}$ ； $② 2^{5} \cdot 2^{5} = 2^{6}$ ； $③ a^{2 m} = (- a^{m})^{2}$ ； $④ a^{2 m} = (- a^{2})^{m} .$ 其中正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
6. 已知 $m = \frac{1 5^{4}}{3^{44}}$ ， $n = \frac{5^{4}}{3^{40}}$ ，那么 $201 6^{m - n} =$ （）

A、 $0$ B、 $1$ C、 $2016$ D、 $201 6^{2}$

查看试题解析
7. 七张如图1的长为 a，宽为 b（a＞b）的小长方形纸片，按图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）

A、a＝b B、a＝2b C、a＝3b D、a＝4b

查看试题解析
8. 已知 $a = 2^{55}$ ， $b = 3^{44}$ ， $c = 4^{33}$ ，则 $a$ 、 $b$ 、 $c$ 的大小关系是（）

A、 $b > c > a$ B、 $a > b > c$ C、 $c > a > b$ D、 $a < b < c$

查看试题解析
9. 已知 $a - b = 5 ， a b = 3$ ，则 $(a + 1) (b - 1) =$ （）

A、3 B、 $- 2$ C、 $- 3$ D、2

查看试题解析
10. 已知 $3^{x} = 4 ， 3^{y} = 6 ， 3^{z} = 12$ ，则x、y、z三者之间关系正确的是（）

A、xy=2z B、x+y=2z C、x+2y=2z D、x+2y=z

查看试题解析

二、填空题

11. 已知2^a=3，2^b=5， 2^c=15，那么a、b、c之间满足的等量关系是

查看试题解析
12. 若27×3^x=3⁹ ，则x的值等于

查看试题解析
13. 如果（x-3）^x=1，则x的值为

查看试题解析
14. 将 $4$ 个数 $a$ ， $b$ ， $c$ ， $d$ 排成 $2$ 行， $2$ 列，两边各加一条竖直线记成 $∣\begin{matrix} a & b \\ c & d \end{matrix}∣$ ，定义 $∣\begin{matrix} a & b \\ c & d \end{matrix}∣ = a d - b c$ ，上述记号就叫做 $2$ 阶行列式 $.$ 若 $∣\begin{matrix} x + 1 & x + 2 \\ x - 1 & x + 3 \end{matrix}∣ = 14$ ，则 $x =$ ．

查看试题解析
15. 长方形的面积是3x²y²－3xy＋6y，宽为3y，则长方形的长是.

查看试题解析

三、计算题

16. 计算：

(1)、（2a³）²+（-a³）²；

(2)、a²•a⁴-a⁸÷a²+（a³）²；

(3)、2a（ab+b²）-3ab（4a-2b）；

(4)、（4a³-6a²+9a）÷2a．

查看试题解析
17. 化简求值

(1)、 $3 a (a^{2} - 2 a + 1) - 2 a^{2} (a - 3)$ ，其中 $a = 2$ ．

(2)、 $(x - 4) (x - 2) - (x - 1) (x + 3)$ ，其中 $x = - \frac{5}{2}$ ．

查看试题解析
18. 计算∶

(1)、 $(4 a - b^{2}) (- 2 b)$

(2)、 $2 x^{2} (x - \frac{1}{2})$

(3)、 $5 a b (2 a - b + 0.2) - (b + 2 a) a b$

(4)、 $(\frac{2}{3} a - \frac{4}{9}) (- 9 a) - a (- 6 a + 4)$

查看试题解析

四、解答题

19. 如图，某小区有一块长为（2a+3b）米，宽为（3a+2b）米的长方形地块，物业公司计划在小区内修一条平行四边形小路，小路的底边宽为a米，将阴影部分进行绿化．

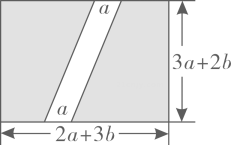(1)、用含有a、b的式子表示绿化的总面积S；

(2)、若a＝2，b＝4，求出此时绿化的总面积S．

查看试题解析
20. 设 $\bar{a b c}$ 是一个三位数，若 $a + b + c$ 可以被3整除，则这个三位数可以被3整除．
证明： $\bar{a b c} = 100 a + 10 b + c$
      $= (99 a + 9 b) + (a + b + c)$
      $= 9 (11 a + b) + (a + b + c)$ ．
      $∵ 9$ 能被3整除， $(11 a + b)$ 是整数，
      $∴ 9 (11 a + b)$ 可以被3整除．
又 $∵ (a + b + c)$ 可以被3整除（已知），
      $∴$ 这个三位数可以被3整除．

(1)、请仿照上面的过程，证明：设 $\bar{a b c d}$ 是一个四位数，若 $a + b + c + d$ 可以被3整除，则这个四位数可以被3整除．

(2)、已知一个两位数的十位上的数字比个位上的数字的2倍大3，这个两位数能否被3整除？如果能，请说明理由；如果不能，请举例说明．

查看试题解析
21. 已知2x+5y-3=0．求4^x·32^y的值。

查看试题解析
22. 仔细阅读下面例题，解答问题：
例题：已知：二次三项式x²﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．
解：设另一个因式为（x+n），得
x²﹣4x+m＝（x+3）（x+n），
则x²﹣4x+m＝x²+（n+3）x+3n
∴ ${\begin{array}{l} n + 3 = - 4 \\ m = 3 n \end{array}$
解得：n＝﹣7，m＝﹣21
∴另一个因式为（x﹣7），m的值为﹣21．
问题：仿照以上方法解答下面问题：
已知二次三项式2x²+3x﹣k有一个因式是（x﹣5），求另一个因式以及k的值．

查看试题解析
23. 已知多项式M除以3x²－2x+4得商式2x+6，余式为3x－1，求多项式M.

查看试题解析